3.2.

ТЕОРИЯ ЗАТРАТ

Каждый предприниматель понимает, что за каждый дополнительный рубль затрат его прибыль уменьшается на 1 рубль. Конечно, можно в погоне за выпуском продукции продолжать бездумно увеличивать затраты, и в какой-то день проснуться банкротом.

При принятии управленческих решений предприниматель должен взвесить, что дешевле – нанять нового работника, или больше платить старому, открыть новое предприятие или расширить действующее. Построить предприятие в России или переместить его заграницу. Все эти решения должны быть оптимальны и направлены на минимизацию затрат. При этом он должен анализировать затраты конкурентов, чтобы их решения не оказались для него неожиданными и роковыми.

Эта глава посвящена пониманию природы затрат, динамики затрат, функциям затрат.

Цели

• Понять природу и сущность затрат и способы их классификации.
• Постичь смысл динамики затрат.
• Освоить теорию затрат, функции затрат.
• Овладеть понятиями постоянных, переменных, общих, предельных, средних затрат.
• Научиться принимать оптимальные решения по управлению затратами предприятия.

Ключевые термины и концепции

• Природа затрат.
• Функции затрат.
• Общие затраты.
• Постоянные затраты.
• Переменные затраты.
• Средние затраты.
• Предельные затраты.

До этого мы изучали производственную функцию Q=f(C,L) и под C,L понимали факторы производства капитал и труд, которые можно представить как затраты (TC). Ими необходимо пожертвовать, чтобы произвести необходимое количество продукции. Таким образом, производственную функцию можно представить как Q=f(TC).

В основе теории затрат положен принцип обратный производственной функции. Этот принцип утверждает, что существует функциональная связь между затратами и объемом производства фирмы, т.е. чтобы произвести определенное количество продукции Q необходимо понести затраты TC, математически данную функциональную связь можно представить в виде: TC=f(Q).

Соответственно, могут существовать и другие независимые переменные, отличные от объема производства, которые могут повлиять на затраты такие, как объем партий изделий, коэффициент использования производственных мощностей, изменения в спросе, конкуренции, цен на вводимые факторы и т.д. При этом предполагается, что затраты, обусловленные этими переменными, остаются постоянными. Соответственно, они считаются постоянными и при построении кривых затрат.

Точная природа (т. е. форма) данной кривой затрат - постоянных, переменных, общих, средних или предельных - зависит от производственной функции для данных цен на вводимые факторы. Полученные таким образом кривые являются статическими, т.е. они показывают лишь то, как меняются затраты с изменением объемов производства при постоянных ценах на вводимые факторы.

Затраты делят на две большие группы - постоянные (fixed) и переменные (variable). Они относятся к общим затратам каждого вида, отнесенным к общему объему производства для данной производственной функции.

Постоянные затраты - это затраты, которые не меняются непосредственно с изменением объема производства, т.е. не являются функцией объема производства. Примерами таких затрат могут служить арендная плата, налоги на собственность и аналогичные выплаты, амортизационные отчисления и т.д. С точки зрения экономиста, синонимом постоянных затрат являются накладные расходы. Для бухгалтера этот термин означает косвенные затраты. Если свести все постоянные затраты фирмы воедино, то получим общие постоянные затраты.

Переменные затраты являются функцией объема производства. Примером переменных затрат являются издержки на материалы, энергию, рабочую силу, комплектующие изделия и т.д. Переменные затраты являются непрерывной функцией объема производства. Если свести все переменные затраты фирмы воедино, то получим общие переменные затраты.

В результате объединив общие переменные, TVC и общие постоянные затраты, TFC получим общие затраты фирмы, TC и это можно выразить формулой:

TC= TFC+ TVC (1)

Таким образом, для получения функциональной зависимости общих затрат от объема производства необходимо рассчитать значения TC, которые соответствуют ряду значений объема производства.

При анализе общие переменные затраты являются единственной меняющейся частью общих затрат, любое изменение суммы явится результатом и будет равно изменению общих переменных затрат. Это изменение, обусловленное изменением объема производства, называется предельными затратами.

Предельные затраты представляют собой изменение общих затрат, вызванное удельным изменением объема производства и равное изменению общих переменных затрат.

Динамика затрат

На затраты влияют два фактора:

1) Характер функции производства.

2) Цены переменных вводимых факторов производства.

Если технология по мере увеличения объема производства остается неизменной (т.е. функция производства не меняется), то результирующие кривые затрат являются зеркальными отражениями соответствующих им функций производства. Следовательно, если одна функция обращена выпуклостью вверх, то другая будет обращена выпуклостью вниз.

Таким образом, форма кривой затрат зависит от формы соответствующей функции производства

Однако положение кривой затрат на графике определяется ценой вводимого фактора X. Если цена возрастет, то кривая затрат смещается вверх, и наоборот.

Чтобы понять структуру затрат фирмы и создать основу для принятия решений по различным вопросам давайте исследуем их.

Введем следующие обзначения:

Q - объем производства;

TC - общие затраты (total costs);

TFC - общие постоянные затраты (total fixed costs);

TVC - общие переменные затраты (total variable costs);

ATC - средние общие затраты (удельные затраты) (average total costs);

AFC - средние (удельные) постоянные затраты (average fixed costs);

AVC - средние (удельные) переменные затраты (average variable costs);

MC - предельные затраты (maximum costs).

Тогда

TC=f(Q)=TFC+TVC (1a)

откуда

AFC=TFC/Q (2)

AVC=TVC/Q (3)

ATC=TC/Q=AFC+AVC (4)
MC=ΔTC/ΔQ для дискретных функций, (5)

MC=dTC/dQ для непрерывных функций. (6)

Как видно из уравнений, TFC влияют на TC и АТС, но не влияют на MC.

Это очевидно, когда мы берем первую производную от постоянной величины – в нашем случае AFC, то по определению производной эта величина будет равна нулю. Давайте докажем, что TFC не влияют на MC:

MC=dTC/dQ=d(TFC+TVC)/dQ=

= dTFC/dQ+dTVC/dQ=0+dTVC/dQ= dTVC/dQ (6a)

В табл. 1. представлены затраты на производство учебников экономики для школ (для получения функции затрат использованы дискретные данные). Данные примера условны.

Таблица 1 Затраты на производство учебников экономики для школ

Объем производства (в тыс. ед.)	Общие постоянные затраты (в тыс. руб.)	Общие переменные затраты (в тыс. руб.)	Общие затраты (в тыс. руб.)	Средние постоянные затраты (в тыс. руб.)	Средние переменные затраты (в тыс. руб.)	Средние общие затраты (в тыс. руб.)	Предельные затраты (в тыс. руб.)
	TFC	TVC	TC=TFC+TVC	AFC=TFC/Q	AVC=TVC/Q	ATC=TC/Q	MC=dTC/dQ
0	600	0	600
1	600	60	660	600	60	660	60
2	600	96	696	300	48	348	36
3	600	126	726	200	42	242	30
4	600	156	756	150	39	189	30
5	600	180	780	120	36	156	24
6	600	216	816	100	36	136	36
7	600	273	873	86	39	125	57
8	600	336	936	75	42	117	63
9	600	432	1032	67	48	115	96
10	600	540	1140	60	54	114	108
11	600	654	1254	55	59	114	114
12	600	782	1382	50	65	115	128
13	600	960	1560	46	74	120	178
14	600	1189	1789	43	85	128	229
15	600	1497	2097	40	100	140	308
16	600	1944	2544	38	122	159	447
17	600	2511	3111	35	148	183	567
18	600	3234	3834	33	180	213	723
19	600	4188	4788	32	220	252	954
20	600	5400	6000	30	270	300	1212

Когда дискретные точки будут соединены между собой, получатся непрерывные нелинейные функции: общих затрат - TC, общих постоянных затрат - TFC, общих переменных затрат - TVC, средних постоянных затрат - AFC, средних переменных затрат - AVC, средних общих затрат - ATC и предельных затрат - MC, представленные на рис. 1.

На рис. 1.а. видно, что общие постоянные затраты TFC, представляют собой прямую линию горизонтальную оси абсцисс. Общие переменные затраты TVC напоминают экспоненциальную кривую. Общие затраты – TC представляют результат суммирования двух кривых.

Кривая средних постоянных затрат (AFC) представляет собой равнобочную гиперболу, которая асимптотически приближается к горизонтальной оси, и это будет справедливо для любой функции общих затрат. Это означает, что AFC непрерывно убывает, как показано на рис. 1.в.

На рис. 1.в. кривые средних переменных затрат (AVC) и средних общих затрат (ATC) также вначале убывают, а затем возрастают. По мере увеличения объема производства кривая ATC приближается к кривой AVC. Это происходит потому, что разность между ними равна удельным постоянным затратам, которые по мере увеличения объема производства становятся все меньше и меньше.

Отметим существенный момент (см. рис. 1.с.), кривая средних общих затрат (ATC), которая вначале убывает, а затем возрастает, пресекается с кривой предельных затрат – MC в точке с объемом производства 11 тыс. учебников. Точка, в которой ATC=MC и ATC=Min, соответствует наиболее эффективному с точки зрения затрат уровню производства учебников для данного вида производства, например, типографии, где учебники будут печататься. Т.е. при дальнейшем увеличении объема производства каждой последующей 1 тысячи учебников (свыше 11 тыс. учебников) затраты на его производство будут устойчиво расти, что не выгодно. В одной из экономических лабораторий данной главы будет решена проблема выпуска продукции с минимальными затратами.

Экономическая лаборатория. Расчет затрат на производство различных учебных пособий для школ.

В табл. 2. представлены затраты на производство различных учебных пособий для школ. Для расчета функции общих затрат использовалось уравнение:

TC=1(Q)⁴-10(Q)³+120(Q)²-20(Q)+6000

Данное уравнение было взято из табл. 2. вариант № 1. Данные примера условны.

Необходимо рассчитать значения:

1. общих затрат - TC, общих постоянных затрат - TFC, общих переменных затрат - TVC, средних постоянных затрат - AFC, средних переменных затрат - AVC, средних общих затрат - ATC и предельных затрат – MC.
2. Построить графики зависимостей, как показано на рис. 1.
3. Ответить на вопросы:
   • Какие выводы можно сделать на основании анализа этих кривых?
   • В чем заключаются некоторые из важнейших свойств этих кривых?

Решение.

Общее решение по варианту 1 приведено в табл. 3.

Некоторые замечания.

Сначала вычисляем TC (колонка 4) для всех значений Q, взятых из колонки 1.

Для определения общих постоянных затрат – TFC известно, что при Q=0 TFC=ТС, в результате получим:

TFC=ТС=1(Q)⁴-10(Q)³+120(Q)²-20(Q)+6000=

=1(0)⁴-10(0)³+120(0)²-20(0)+6000=6000

Вычислив TFC, не составляет труда определить все значения TVC.

Все расчеты сведены в таблицу 3.

Таблица 3. Затраты на производство учебников экономики для школ

Построим графики:

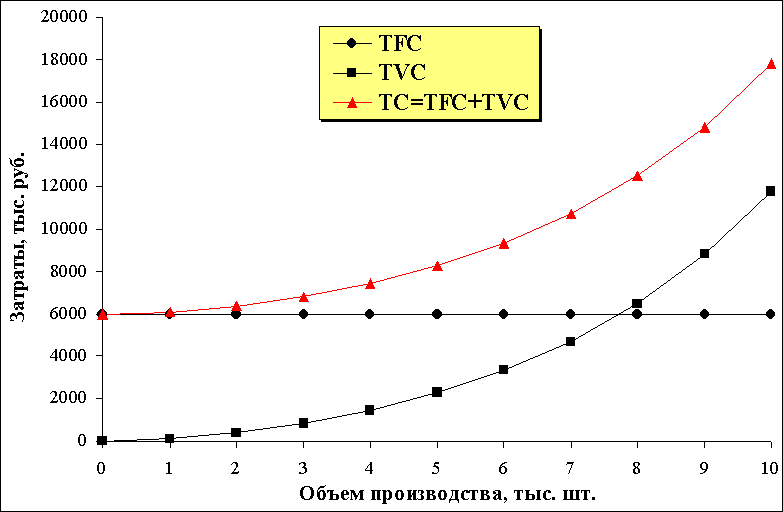
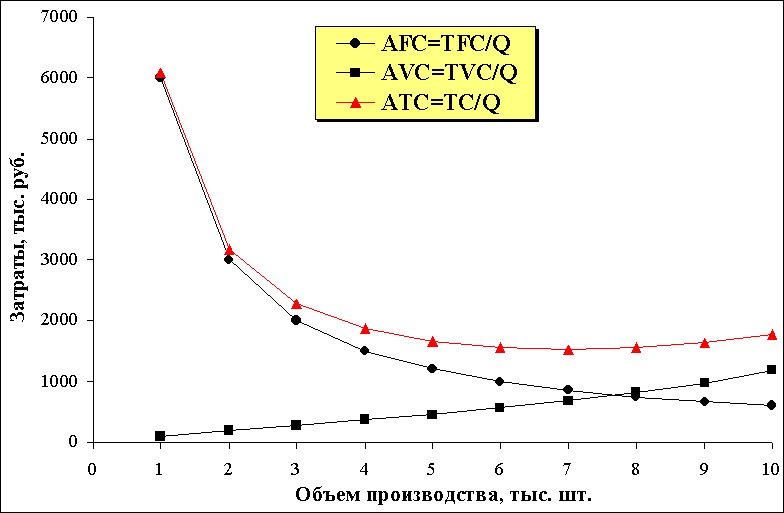
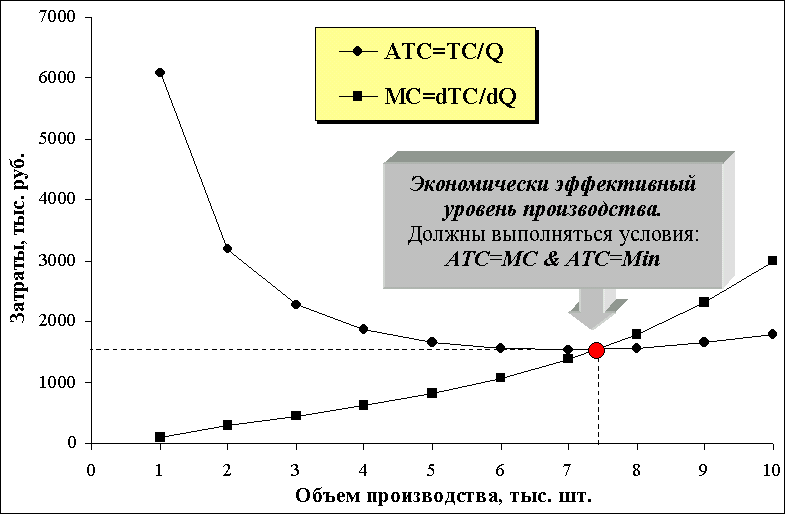
Рис. 2. Затраты на производство учебных пособий для школ.

Затраты и производство

Как отмечалось ранее, производственная функция определяется технической природой и соответствующих им кривых производства, а не ценой факторов производства. Учитывая, что функции затрат противоположны производственной функции, то формы кривых средних и предельных затрат, так же как и общих переменных затрат, которые графически можно представить перевернутым отображением.

Изменение цен факторов производства сдвинет кривые на графике вверх или вниз, а не повлияет на их наклоны и, следовательно, формы. На рис. 3. наглядно видно, что с ростом цен переменных факторов производства кривые средних и предельных затрат сдвинулись верх.

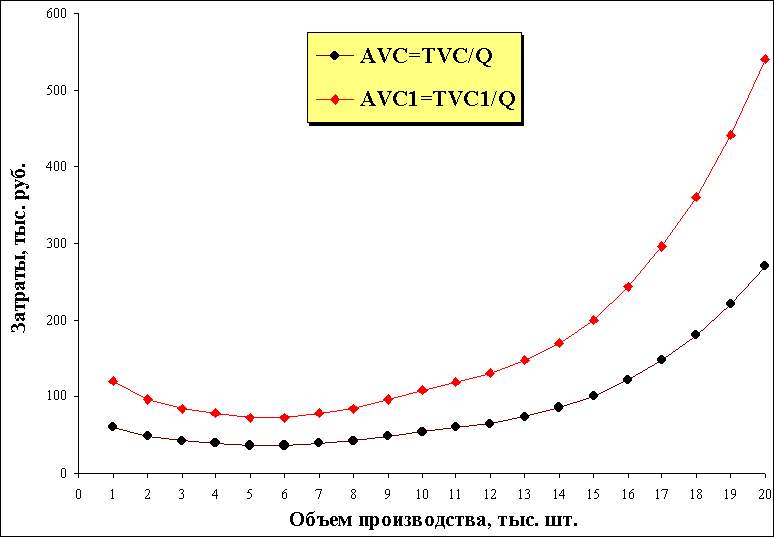
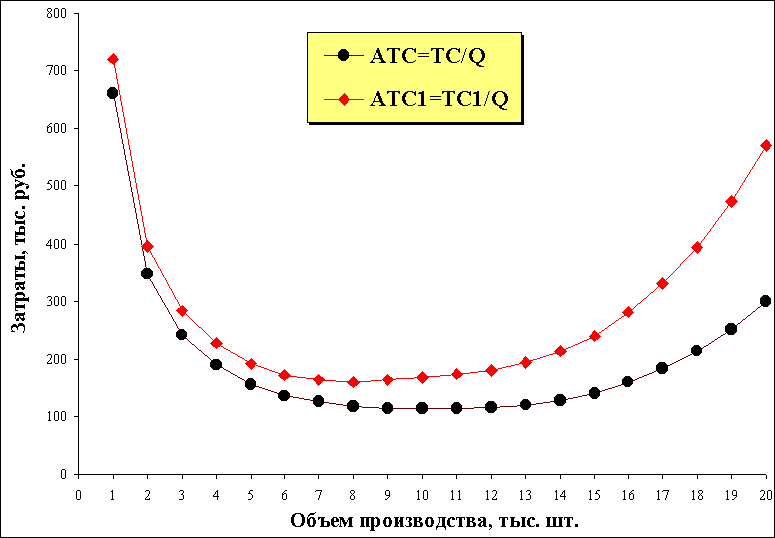
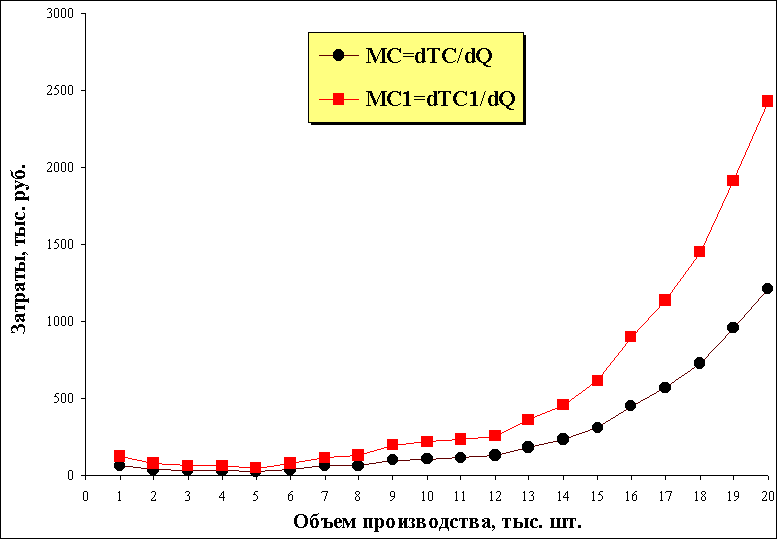
Рис. 3. Рост цен переменных затрат на 100%.

Следствием того, что цена факторов не зависит от объема производства, является обратное соотношение между:

1) Средними переменными затратами и средним продуктом.

2) Предельными затратами и предельным продуктом.

Для вывода соответствующих соотношений проделаем следующее.

1. Средние переменные затраты связаны с объемом производства следующим соотношением:

AVC_Q=TVC_Q/Q_Х=(P_ХХ)/Q_Х=P_Х (Х/Q_Х) (1)

где AVC_Q - средние переменные затраты для объема производства;

TVC_Q - общие переменные затраты для объема производства;

Q_Х - объем производства в единицах измерения для вводимого фактора Х;

P_Х - удельная цена вводимого фактора X;

X - количество единиц вводимого фактора X.

Средний продукт, AP_Х, определяется как Q_Х/X, т.е. обратно пропорционален X/Q_Х в уравнении (1). Следовательно, средние переменные затраты могут быть определены как:

AVC_Q=P_Х (1/(Q_Х/Х))=P_Х/AP_X (2)

Полагая, что цена вводимого фактора постоянна, из уравнения (2) следует, что, когда AP_X увеличивается, AVC_Q уменьшается и наоборот. Следовательно, когда AVC_Q достигают минимума, AP_Х максимален.

2. Кроме того, очевидно обратное соотношение между предельным продуктом и предельными затратами, которое не зависит от постоянных вводимых ресурсов. Следовательно, предельные затраты, MC_Q, могут быть определены как

MC_Q =ΔTVC_Q/ΔQ_Х=(ΔХ P_Х) /ΔQ_Х=

= P_Х(ΔХ/ΔQ_Х)= P_Х (1/(ΔQ_Х/ΔХ))=P_Х/MP_X (3)

Если цена вводимого фактора постоянна, то из уравнения (3) следует, что когда MP_X увеличивается, MC_Q уменьшается и наоборот. Следовательно, MC_Q минимальны при максимальном MP_Х.

3. Средние общие затраты, ATC_Q являются суммой средних постоянных затрат, AFC_Q, и средних переменных затрат, AVC_Q, т.е.

ATC_Q = AFC_Q + AVC_Q. (4)

4. Очевидно, что чем больше объем производства, тем меньше AFC. Следовательно, кривая ATC асимптотически приближается к кривой AVC. Мы можем также заметить, что самая нижняя точка этой кривой соответствует большему объему производства, чем в точке минимума AVC. Это связано с тем, что когда объем производства впервые превышает уровень, соответствующий минимуму AVC, спад AFC вызывает усиленный рост AVC. Однако по мере увеличения объема производства мы достигаем точки, в которой увеличение AVC превышает спад AFC. В этой точке кривая АТС устремляется вверх.

5. Наиболее экономически эффективному уровню производства соответствует точка, в которой MP_Х = AP_Х, a AP_Х проходит через максимум. Эта точка соответствует окончанию стадии 1 и началу стадии 2 классической производственной функции, представленной на рис. 1. в главе 2, и совпадает с уровнем, в котором MC=ATC, и соответствует минимуму средних полных затрат – АТС (см. рис. 1.в.).

Экономическая лаборатория. Расчет производственных затрат

Вам поручили исследовать производственный процесс. После изучения данного производства вы получили следующие данные:

1. Для изготовления одного изделия требуется затратить 10 ч (колонка 1) и использовать сырья на 45 долл. (колонка 2).
2. В настоящее время уровень производства фирмы составляет 894 изделий в неделю (колонка 3) при продолжительности рабочего года, составляющей 50 недель (колонка 4).
3. Продолжительность рабочей недели 40 часов (колонка 5).
4. Постоянные затраты составляют 110110 долл. в год (колонка 6).
5. Заработная плата производственного рабочего равна 7 долл. в час (колонка 7), включая налог на заработную плату, пенсионные отчисления и другие выплаты. Кроме того, каждый рабочий имеет ежегодный оплачиваемый отпуск продолжительностью в две недели.

Исходные данные взяты из табл. 4. вариант 1.

Вопросы.

а. Каковы средние (удельные) переменные затраты для данного производства?

б. Каковы общие удельные затраты?

Решение.

а. Сначала определим общую почасовую заработную плату, включая оплачиваемый отпуск.

Для каждого рабочего годовая заработная плата, включая оплаченный отпуск, составляет:

w_Год = (N_нед +2)* Нед_(час)* w_час = 52*40*7= 14560.

Тогда почасовая оплата равна:

w_(час) = w_Год : N_нед : Нед_(час) = 14560 : 50 рабочих недель : 40ч=7,28 в час.

Средние переменные затраты связаны с объемом производства следующим соотношением:

AVC_Q=TVC_Q/Q_Х=(P_ХХ)/Q_Х=P_Х (Х/Q_Х) (5)

где AVC_Q - средние переменные затраты для объема производства;

TVC_Q - общие переменные затраты для объема производства;

Q_Х - объем производства в единицах измерения для вводимого фактора Х;

P_Х - удельная цена вводимого фактора X;

X - количество единиц вводимого фактора X.

Средний продукт, AP_Х, определяется как Q_Х/X, т.е. обратно пропорционален X/Q_Х в уравнении (1). Следовательно, средние переменные затраты могут быть определены как:

AVC_Q=P_Х (1/(Q_Х/Х))=P_Х/AP_X=

= (T_час w_(час)+ TVC)/1изделие=((10)(7,28)+45)/1=117,8 долл. за изделие

б. Годовой объем производства определяется следующим образом:

Q_Год = V_нед N_нед = 894 изделий в неделю * 50 недель = 44700 изделий.

Тогда удельные постоянные затраты составят:

AFC_Q = TFC/Q_Год = 110110/44700 изделий = 2 долл. за изделие.

Средние общие затраты, ATC_Q являются суммой средних постоянных затрат, AFC_Q, и средних переменных затрат, AVC_Q, т.е.

ATC_Q = AFC_Q + AVC_Q=2+117,8≈120 долл. за изделие.

В приведенной таблице 4. выберете свой вариант. Проведите вычисления и полученные результаты сравните с ответами.

Экономическая лаборатория. Эффективный уровень производства

По просьбе руководства компьютерной фирмы вы исследовали производство и построили функцию общих затрат:

TC=120Q-4Q²+0,16Q³ (колонка 1)

Исходные данные взяты из табл. 5. вариант 1.

Вы должны рекомендовать руководителю фирмы, сколько компьютерных систем должна производить в смену его фирма, чтобы достичь наиболее эффективного уровня производства.

Вопросы.

а. Определите объем производства, для которого удельные затраты минимальны ATC_Qmin.

б. Определите объем производства, для которого предельные затраты минимальны MC_Qmin.

в. Определите эластичность затрат, если Q=4, Q=38, а также эластичность в точках ATC_Qmin и MC_Qmin.

Решения

а. Удельные затраты равны средним общим затратам

ATC=TC/Q=(120Q-4Q²+0,16Q³)/Q= 120-4Q+0,16Q²

Объем производства, при котором удельные затраты минимальны, можно определить, вычислив первую производную функции АТС, приравняв ее к нулю и решив полученное уравнение относительно Q:

dATC/dQ=-4+(0.16)(2)Q=-4+0.32Q=0

Q=4/0,32=12,5

б. Предельные затраты - это первая производная функции общих затрат:

MC=dTC/dQ=d(120Q-4Q²+0,16Q³)dQ=120-8Q+0.48Q²

Для того, чтобы найти уровень производства, соответствующий минимуму предельных затрат, возьмем первую производную функции MC, приравняем ее к нулю и решим полученное уравнение относительно Q:

dMC/dQ=-8+2(0.48)Q=-8+0.96Q

Q=8/0.96=8.33

в. Эластичность затрат при Q=4, Q=38, а также эластичность в точках ATC_Qmin и MC_Qmin:

ε_Q0=4=MC/ATC=(120-8Q+0.48Q²)/(120-4Q+0,16Q²)=

=(120-8(4)+0.48(4)²)/(120-4(4)+0,16(4)²)=0.90

Соответственно:

ε_MC=0,89, при Q≈8

ε_ATC=1, при Q=12.5≈13

ε_Q1=38=2,56, при Q≈38

Как видно из полученных данных, с ростом производства затраты начиная с Q>13 растут более интенсивно, чем производство продукции. Так при Q>38 рост на 1% производства Q будет приводить к росту на 2,56% затрат при производстве продукции.

Наиболее эффективный уровень производства с точки зрения затрат достигается при объеме выпуска Q=12.5≈13. При этом уровне производства выполняются два условия ATC=MC и ATC=Min.

Рекомендация руководителю компьютерной фирмы:

Производственные подразделения фирмы должны производить в смену 12-13 компьютерных систем, это позволит достичь наиболее эффективного уровня производства. Если фирма желает расширить производство, то необходимо создавать новые производства с объемами выпуска в пределах 12-13 компьютерных систем в смену, при условии, если функция общих затрат буде сохранена в виде TC=120Q-4Q²+0,16Q³

В приведенной таблице 5. выберите свой вариант. Проведите вычисления и полученные результаты сравните с ответами.

Таблица 5.
№	Исходные данные			Ответ
	TC	Q0	Q1	ATCQmin	MCQmin	εATC	εMC	εQ0	εQ1
0	TC=100Q-3Q^2+0,1Q^3	5	30	15	10	1	0,88	0,89	1,90
1	TC=120Q-4Q^2+0,16Q^3	4	38	12,50	8,33	1,00	0,89	0,90	2,56
2	TC=1157Q-8Q^2+0,06Q^3	22	200	66,67	44,44	1,00	0,87	0,88	2,64
3	TC=864Q-2Q^2+0,07Q^3	5	43	14,29	9,52	1,00	0,99	0,99	1,19
4	TC=754Q-10Q^2+0,15Q^3	11	100	33,33	22,22	1,00	0,88	0,89	2,59
5	TC=1081Q-7Q^2+0,09Q^3	13	117	38,89	25,93	1,00	0,94	0,94	2,10
6	TC=1078Q-9Q^2+0,15Q^3	10	90	30,00	20,00	1,00	0,94	0,94	2,09
7	TC=785Q-6Q^2+0,19Q^3	5	47	15,79	10,53	1,00	0,97	0,97	1,60
8	TC=1430Q-2Q^2+0,18Q^3	2	17	5,56	3,70	1,00	1,00	1,00	1,05
9	TC=1156Q-9Q^2+0,08Q^3	19	169	56,25	37,50	1,00	0,88	0,89	2,59
10	TC=701Q-6Q^2+0,08Q^3	13	113	37,50	25,00	1,00	0,92	0,92	2,31

Экономические недостатки, обусловленные увеличением масштаба производства (на уровне завода)

Когда завод (фирма) становится слишком большим, могут возникнуть недостатки, обусловленные увеличением масштаба производства.

1. Появляются «узкие» места в технологическом процессе.

2. За счет трудностей при подвозе материалов, перемещении их внутри завода и вывозе за его пределы могут увеличиться транспортные расходы.

3. Распределение увеличивающихся объемов готовой продукции может оказаться более дорогостоящим.

4. По мере увеличения размеров предприятия уменьшается координация действий и усложняется контроль.

5. Удаленность фирмы от потребителей увеличивает риски и невозможность выполнения заказа в короткие сроки, это может привести к росту запасов, складских затрат и в конечном счете приведет к потере рынка.

В предыдущей экономической лаборатории было показано, что если компьютерная фирма желает расширить производство, то необходимо создавать новые производства с объемами выпуска в пределах 12-13 компьютерных систем в смену, при условии, если функция общих затрат будет сохранена в виде:

TC=120Q-4Q²+0,16Q³

При таком выпуске компьютерных систем достигается наиболее эффективный уровень производства.

Рассмотрим эту проблему подробнее.

Экономическая лаборатория. Создание новых "заводов, производств, фирм"

Фирма «АБВГД» производит 10 тип компьютерных систем и поставляет их своим потребителям по всей России и СНГ. География поставок фирмы представлена на рис. 4.

В настоящее время все компьютерное производство фирмы сосредоточено на одном предприятии, расположенном в Калининграде.

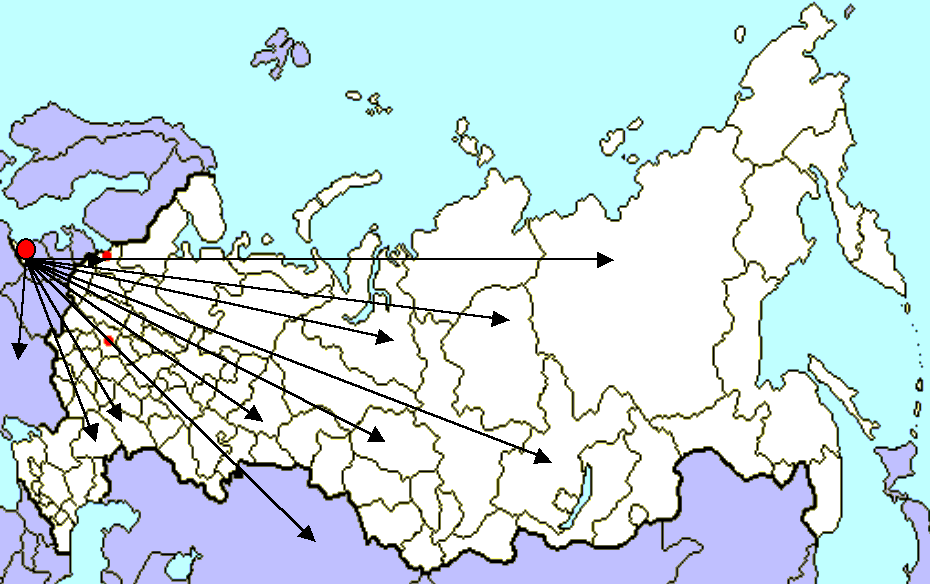
Рис. 4. Карта поставок фирмы "АБВГД"

Руководитель фирмы «АБВГД» поручил вам исследовать его производство и выдать рекомендации по эффективному управлению фирмой.

Проанализировав карту поставок фирмы (рис. 4.), вы обнаружили высокие транспортные расходы фирмы, устойчивый рост сроков поставки продукции потребителям и т.д.

На основании своего предыдущего опыта работы (глава 1), вы исследовали рынок фирмы и установили:

Устойчивое увеличение спроса на все виды компьютерных систем фирмы.

Вы также построили функции спроса по каждому изделию фирмы.

Кроме этого вы сформировали рабочую гипотезу:

"О целесообразности создании нескольких заводов (производств), приближенных к потребителям и потенциальным рынкам сбыта".

Согласно вашим исследованиям, спрос на первое изделие равен:

P = 1800 - 0,018Q.

Изучив производство по каждому изделию, вы сформировали функции общих затрат, включая производство и транспортировку.

Для первого изделия функция следующая:

TC = 600000+60Q+0,012Q².

Проведенный дополнительный анализ показал, что при переходе к производству 10 изделий на нескольких предприятиях функция затрат сохранится.

Зная спрос можно определить функцию общего дохода предприятия (выручки) TR, который будет равен произведению спроса на объем продаж:

TR= PQ=1800Q-0.018Q²

Определим предельные затраты MC_Q:

MC_Q=dTC/dQ=d(600000+60Q+0,012Q²)/dQ=

=60+2*0.012Q=60+0.024Q

Предельный доход (MR_Q) представляет собой дополнительный добавочный доход, получаемый в результате продажи одной дополнительной единицы продукции.

Для дискретной функции MR_Q будет равен:

MR_Q=ΔTR/ΔQ

Для непрерывной функции MR_Q будет равен:

MR_Q=dTR/dQ=1800-2*0.018Q=1800-0.036Q

Уровень производства для одного предприятия, который обеспечивает максимальную прибыль, равен такому уровню, при котором предельный доход равен предельным затратам:

MR_Q= 1800-0.036Q=60+0.024Q= МС;

-0,06Q = -1740;

Q = 29000 изделий (колонка 1).

Оптимальная цена определяется как:

P =1800 - 0,018Q=1800 - 0,018(29000) = 1278 за изделие (колонка 2).

Максимальная прибыль составляет

Pr=TR-TC=PQ-TC=1278(29000)-600000-60(29000)-0,012(29000)²=24630000 (колонка 3).

Если фирма выберет стратегию, предусматривающую эксплуатацию нескольких заводов, то она пожелает, чтобы каждый из них имел эффективный масштаб производства, который соответствует самым низким из возможных удельных затрат:

ATC=TC/Q=(600000+60Q + 0,012Q²)/Q=600000Q^-1+60+0,012Q

dATC/dQ=-1*600000Q^-1-1+ 0,012=-600000Q^-2+ 0,012=0

0,012Q² = 600000;

Q² =600000/0,012;

Q≈7071 (колонка 4).

Следовательно, эффективный минимальный масштаб производства для заводов фирмы будет равен стандартной операционной мощности около 7100 изделий. На этом уровне MC и АТС примерно равны и ниже, чем у предприятия с мощностью 30000 изделий. Более того, как следует из рис. 5., предельные затраты для всей производственной цепочки фирмы будут одинаковыми.

Для объема производства в 29000 изделий:

MC=60+0.024Q=60+0.024(29000)=756 (колонка 5).

Для объема производства в 7071 изделий

MC = 60+0.024Q=60+0.024(7071)=230 (колонка 6).

Как показано на рис. 5., распределение общего объема производства между несколькими предприятиями вместо одного крупного завода позволяет фирме обеспечить постоянные предельные затраты, которые равны средним общим затратам при эффективном масштабе производства.

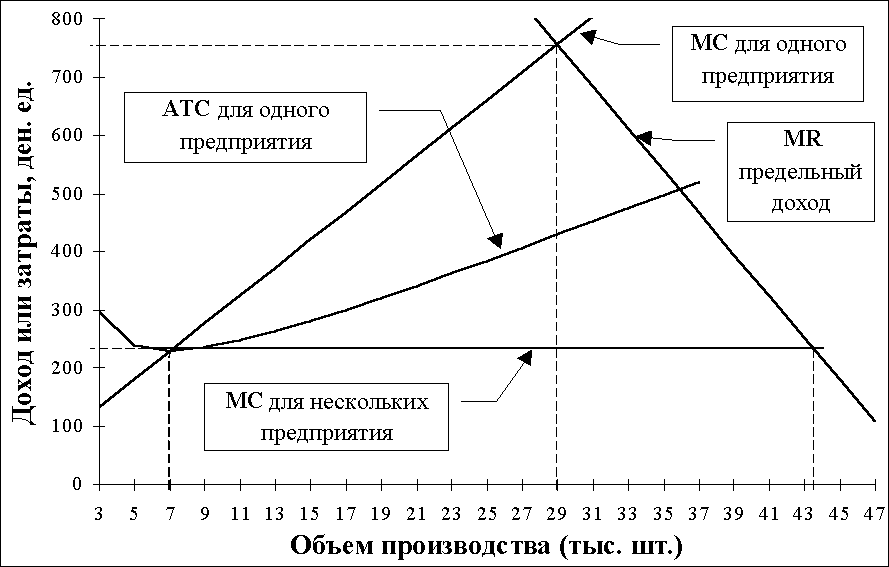
Рис. 5. Предельные затраты, средние общие затраты и предельный доход для одного предприятия, выпускающего 29000 изделий, и шести предприятий с мощностью 7071 изделий каждое.

В данном исследовании уровни производства и реализации, позволяющие максимизировать прибыль, будут равны такому объему производства, при котором предельный доход равен предельным затратам, составляющим 230 долл.

MR=1800-0.036Q=230;

-0,036Q =-1570;

Q = 43619 изделий (колонка 7).

Для обеспечения такого объема производства потребуется:

N_Plant=43619/7071≈6 заводов (колонка 8) с мощностью 7071 изделий каждый. Общие затраты на производство 43619 изделий составят:

ТС_N= N_Plant(500000+80Q+0,01Q²)=

=6(500000+80(7071)+0,01(7071)²)≈9745491 (колонка 9).

Для того чтобы продать 43619 изделий, нужно снизить цену до:

P_N=1800-0,018Q=1800-0,018(43619)=1015 (колонка 10),

что на 263 долл. меньше оптимальной цены при производстве всех изделий на одном предприятии, равной 1278 долл.

Прибыль фирмы при разворачивании 6 производств в непосредственной близости к потребителям составит:

PR_N=TR-TC=PQ-TC=1015(43619)-9745491=34521600 (колонка 11).

Это на 9 891 600 долл. (колонка 12) больше прибыли, которая получается при выпуске 29000 изделий на одном заводе (такая прибыль составляет 24630000 долл.).

Выводы и рекомендации для руководителя фирмы "АБВГД":

"Фирме для эффективного управления и производства целесообразно создать 6 небольших предприятий, приближенных к потребителям и потенциальным рынкам сбыта".

При проведении расчетов предполагалось, что каждое из шести предприятий несет одинаковые постоянные затраты, равные постоянным затратам одного крупного предприятия. Если постоянные затраты каждого из небольших заводов могут быть снижены, то увеличение прибыли может быть еще большим.

В приведенной таблице 7. выберете свой вариант. Проведите вычисления и полученные результаты сравните с ответами.