3.1.
ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ
В данной главе мы должны научиться
принимать оптимальные решения по
использованию ресурсов предприятия на
основе изучения производственной
функции.
Чтобы исследовать производство,
необходимо установить количественные
соотношения между используемыми
факторами производства (ресурсами)
и уровнем выпуска продукции.
Предприятие должно найти такое сочетание
вводимых ресурсов, при котором достигается
оптимизация производственного процесса.
Мы поймем, почему увеличение не
заработанной заработной платы всегда
приводит к уменьшению численности
персонала и как фирма, стремящаяся к
максимизации прибыли, будет замещать
труд капиталом.
Цели.
- Понять сущность производственной
функции и ее математическое выражение.
-
Понять основные категории: постоянные
и переменные факторы производства.
-
Описать три стадии производственной
функции, эластичность производства.
-
Освоить закон убывающей доходности.
-
Постичь смысл предельного дохода,
издержек, продукта.
-
Научиться принимать оптимальные решения
по использованию ресурсов предприятия.
Ключевые термины и концепции.
- Производственная функция.
-
Постоянные, переменные факторы
производства.
-
Закон убывающей доходности.
-
Эластичность производства.
-
Предельный доход.
-
Предельные издержки.
-
Предельный продукт.
Производственные функции
Под производственной функцией
понимается взаимозависимость «затраты
- выпуск» между одним или несколькими
вводимыми факторами производства и
производимыми товарами или услугами
(выпуском продукции).
Термин «производство» означает
процесс превращения вводимых факторов
производства, таких, как труд и
капитал (деньги, материалы, земля,
здания, оборудование) в готовую
продукцию.
Готовая продукция может представлять
собой товары для конечного потребления,
готовые для реализации потребителю,
или промежуточные товары, для
дальнейшего использования и производства
из них товаров для конечного потребления.
По аналогии с функцией спроса,
производственная функция может быть
представлена в виде таблицы, графически
или аналитически в виде следующего
уравнения:
Q= (X1,
X2 ,..., Xn) (1)
где Q - выпуск продукции,
X1, X2,...,
Xn - вводимые факторы
производства.
Например, величины X1, X2
могут означать труд рабочих и служащих,
который затрачен на производство
выпускаемой продукции; X3,X4,X5,X6,X7,
- средства производства, такие, как
земля, здания, станки, компьютеры и т.д.;
X8 - сырье,X9,..,Xn
– технологии производства, управления
и т.д.
Вводимые факторы производства
для каждой фирмы индивидуальны и
их количество и качество различны.
Все перечисленные вводимые факторы
производства можно сгруппировывать в
два фактора: капитал С, и труд
L, в результате производственная
функция можно представить уравнением:
Q=f(C, L). (2)
Вводимые факторы производства могут
быть подразделены на две категории:
постоянные факторы производства и
переменные факторы производства.
Постоянные факторы производства
представляют собой в большинстве случаев
капитальные ресурсы (такие, как земля,
здания (строения) и оборудование),
количество которых условно не меняется
в течение рассматриваемого периода.
Переменные факторы производства
представляют собой те вводимые ресурсы,
количество которых непосредственно
связано с уровнем выпуска продукции. К
ним можно отнести количество затраченного
труда персонала, сырье, материалы,
киловатт-часы электроэнергии. Они могут
увеличиваться или уменьшаться в
зависимости от предполагаемого уровня
выпуска продукции.
Экономическая лаборатория
Исследование производственной
функции
Цель данной экономической лаборатории
научиться на практике не только таблично,
графически, но и аналитически исследовать
производственную функцию.
Предположим, что опытная сельскохозяйственная
станция планирует провести исследование
влияния у добрений
на производство картофеля. Наряду с
удобрениями, урожай картофеля зависит
от целого ряда других факторов
производства, таких, как почва
(земля), вода (дождевая или вода для
орошения), солнечный свет, температура
и труд. Но в данном исследовании в
качестве переменного фактора производства
используются только удобрения.
добрений
на производство картофеля. Наряду с
удобрениями, урожай картофеля зависит
от целого ряда других факторов
производства, таких, как почва
(земля), вода (дождевая или вода для
орошения), солнечный свет, температура
и труд. Но в данном исследовании в
качестве переменного фактора производства
используются только удобрения.
Предположим, что исследователи создали
двенадцать опытных делянок и на каждой
из них высадили картофель одного и того
же сорта.
Первую делянку исследователи используют
в качестве контрольной, на которую не
вносят никаких удобрений. На других
делянках они внесут удобрения с таким
расчетом, чтобы на каждой из последующих
делянок количество вносимых удобрений
увеличивалось. Когда наступает время
уборки урожая, картофель, собранный на
каждой из делянок, взвешивается отдельно.
Затем полученные по всем участкам
результаты сводятся в одну таблицу,
чтобы их можно было сравнивать, анализируя
итоги исследования. Результаты
представлены в табл. 1.
Таблица 1 Производство картофеля
на опытных делянках
|
№ делянки |
Количество удобрений, мешков |
Общий выпуск продукции, кг. |
Средний выпуск продукции, кг./ мешок |
Предельный продукт, кг. |
Эластичность производства |
Производная предельного продукта |
|
|
Х |
Q |
APХ=Q/X |
MPХ=dQ/dX |
εР=MPХ
/APХ |
MPХ'=dMPХ
/dX |
|
1 |
0 |
850 |
|
|
|
|
|
2 |
1 |
2727 |
2727 |
1877 |
0,69 |
|
|
3 |
2 |
6020 |
3010 |
3293 |
1,09 |
1416 |
|
4 |
3 |
10255 |
3418 |
4235 |
1,24 |
942 |
|
5 |
4 |
14958 |
3740 |
4703 |
1,26 |
468 |
|
6 |
5 |
19655 |
3931 |
4697 |
1,19 |
-6 |
|
7 |
6 |
23872 |
3979 |
4217 |
1,06 |
-480 |
|
8 |
7 |
27135 |
3876 |
3263 |
0,84 |
-954 |
|
9 |
8 |
28970 |
3621 |
1835 |
0,51 |
-1428 |
|
10 |
9 |
28903 |
3211 |
-67 |
-0,02 |
-1902 |
|
11 |
10 |
26460 |
2646 |
-2443 |
-0,92 |
-2376 |
|
12 |
11 |
21167 |
1924 |
-5293 |
-2,75 |
-2850 |
В таблице 1. наряду с общим выпуском
продукции (Q) (сколько собрано
картофеля) - колонка 2, указаны четыре
других важных показателя: средний
выпуск продукции - колонка 3 и предельный
продукт - колонка 4, эластичность
производства - колонка 5, производная
предельного продукта - колонка 6.
Средний выпуск продукции (APХ)
представляет собой частное от деления
общего выпуска продукции на
количественное значение переменного
вводимого фактора производства,
т.е. APХ=Q/X.
Предельный продукт (MPХ)
представляет собой изменение общего
выпуска продукции, деленное на изменение
переменного вводимого фактора
производства, т.е. MPХ=ΔQ/ΔХ.
Хотя величины MPХ определены
путем вычислений с использованием
дискретных значений величины X,
единицы вводимого фактора производства
(мешки удобрения) являются бесконечно
делимыми (их можно рассыпать до гранулы
удобрения), поэтому основная функция
является непрерывной, т.е. MPХ=dQ/dХ.
Это означает, что соотношения,
представленные в табл. 1, можно рассматривать
как отдельные точки, принадлежащие
кривым, изображенным на рис. 1. Это также
означает, что для анализа производственной
функции и ее связи со средним выпуском
продукции, предельным продуктом,
эластичностью, производной предельного
продукта можно воспользоваться
аналитическими методами.
На рис. 1. показаны соотношения между
общим выпуском продукции - TPX,
предельным продуктом - MPХ,
средним выпуском продукции - APХ,
и эластичностью производства - εР,
при условии, что изменяется только
один из вводимых факторов производства,
в то время как все остальные вводимые
факторы остаются постоянными или
их изменения были одинаковы для всех
делянок. Например, прошел дождь, который
оросил все делянки одновременно.
По оси абсцисс на рис. 1. отложены
количественные значения переменного
вводимого фактора производства, X,
т.е. расход удобрений в мешках.
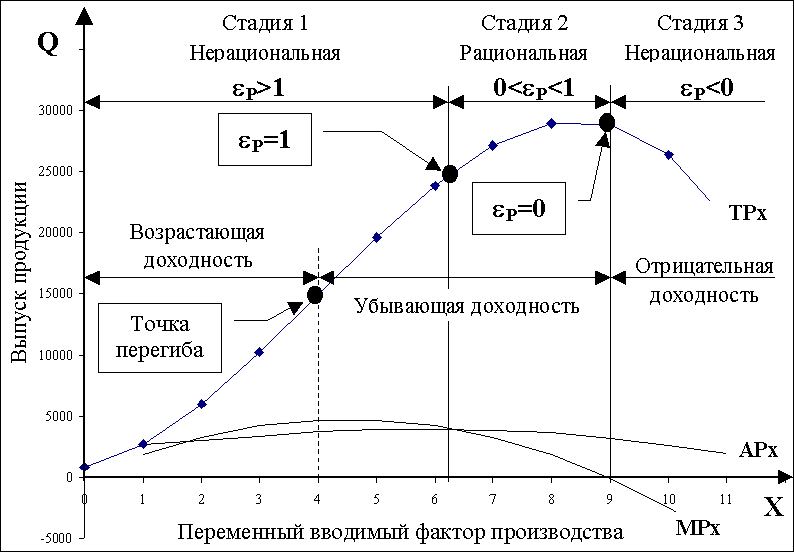
Рис. 1.Производственная
функция
По оси ординат отложены значения
выпуска продукции (сбор картофеля), Q,
в кг.. Верхняя кривая, TPХ,
представляет собой графическое
изображение функции производства,
Q=f(X1|X2,X3,...,XN).
Изучив кривую общего выпуска продукции,
TPX=Q=f(X) исследователи
установили, что ее лучше всего описать
кубическим уравнением:
Q=a+bX+cX2+dX3=
850+1011X+945X2-79X3 (3)
Под TPX расположены кривые
функции среднего выпуска продукции,
APХ=Q/X, и функции
предельного продукта, MPХ=dQ/dX.
Поскольку в табл. 1. содержатся только
дискретные значения величин X
и Q, соответствующие значения MPХ
в таблице вычислялись как ΔQ/ΔХ. Для
непрерывной функции, изображенной
на рис. 1. в виде кривой общего выпуска
продукции, TPX=Q=f(X),
предельный продукт является ее
производной, dQ/dX.
Какие выводы можно сделать на основании
анализа этих кривых?
В чем заключаются некоторые из важнейших
свойств производственной функции?
Закон убывающей доходности
Как следует из рис. 1., с каждой
дополнительной единицей вводимого
фактора Х возрастает выпуск продукции
вплоть до некоторой точки Х≥9,
за пределами которой дальнейший прирост
вводимого фактора Х ведет к сокращению
выпуска продукции.
Закон убывающей доходности
справедлив, по существу, для всех типов
производственных функций, изменяющихся
в широких пределах: от характерных для
сельскохозяйственного производства и
автомобильных заводов и до встречающихся
в розничной торговле, на текстильных
фабриках, на предприятиях по добыче
полезных ископаемых и на предприятиях
сферы услуг и т.д.
 Закон убывающей доходности представляет
собой явление исключительной важности,
применимое ко всем видам производства.
Закон убывающей доходности представляет
собой явление исключительной важности,
применимое ко всем видам производства.
Соотношение «общий выпуск продукции
- предельный продукт» TPХ ↔MPХ
Кривые, представленные на рис. 1.,
позволяют с большой наглядностью
установить соотношения между предельным
продуктом MPХ и общим
выпуском продукции TPХ.
Анализ кривых на рис. 1. позволяют сделать
следующие выводы:
- возрастающая доходность имеет
место при возрастании переменного
вводимого фактора производства Х
до тех пор, пока функция предельного
продукта MPХ положительна
и возрастает и достигает своего максимума
при значения Х=4;
-
убывающая доходность имеет место
до тех пор, пока функция MPХ
положительна и убывает;
-
отрицательная доходность имеет
место, когда функция предельного
продукта MPХ отрицательна
и убывает при значения Х≥9.
Соотношение «средний выпуск продукции
- предельный продукт» АPХ↔MPХ
Кривые на рис. 1. позволяют установить
количественное соотношение между
средним выпуском продукции АPХ
и предельным продуктом MPХ.
1. Средний выпуск продукции АPХ
возрастает при возрастании переменного
вводимого фактора производства Х
до тех пор, пока значение функции
предельного продукта MPХ
превышает соответствующее среднее
значение выпуска продукции. На рис. 1.
это соответствует изменению переменного
вводимого фактора производства в
пределах от 1 до 6,2 единиц.
2. Когда предельный продукт MPХ
становится меньше среднего выпуска
продукции АPХ, последний
уменьшается при дальнейшем возрастании
величины переменного вводимого фактора
производства. На рис. 1. указанное
соотношение имеет место при величине
вводимого фактора Х, превышающего
6,2 единиц.
3. Когда функция среднего выпуска
продукции АPХ достигает
максимума, величина среднего выпуска
продукции и величина предельного
продукта MPХ становятся
равными. Согласно графику,
представленному на рис. 1., это происходит
при значении вводимого фактора
производства, равном 6,2 единицам.
Функция среднего выпуска продукции
АPХ достигнет своего
максимального значения тогда, когда
величина предельного продукта MPХ
и величина среднего выпуска продукции
станут равны между собой (MPХ=APХ).
Отвечающая этому событию точка и
является точкой, соответствующей
максимальной эффективности производства
при одном переменном вводимом факторе
производства, в нашем примере - это
удобрения.
 Максимальная эффективность производства
достигается при таком конкретном
значении переменного вводимого фактора
производства X, когда сам этот переменный
фактор может быть использован наиболее
эффективно в сочетании со всеми прочими
вводимыми факторами производства,
которые сохраняются неизменными.
Максимальная эффективность производства
достигается при таком конкретном
значении переменного вводимого фактора
производства X, когда сам этот переменный
фактор может быть использован наиболее
эффективно в сочетании со всеми прочими
вводимыми факторами производства,
которые сохраняются неизменными.
Три стадии производства
На рис. 1. также хорошо проиллюстрированы
три типичные стадии производственной
функции.
Стадия 1. Настоящая стадия охватывает
интервал от значения переменного
вводимого фактора производства, X,
равного нулю, до такого его значения,
которое соответствует максимальному
значению функции среднего выпуска
продукции - APХ. Выпуск
продукции может быть увеличен за счет
дальнейшего увеличения численных
значений переменного вводимого фактора
производства по отношению к постоянным
вводимым факторам производства. При
этом средний выпуск продукции - APХ
является мерой эффективности.
 Эффективность производства может быть
повышена за счет увеличения переменного
вводимого фактора производства.
Эффективность производства может быть
повышена за счет увеличения переменного
вводимого фактора производства.
Стадия 2. Как следует из рис. 1., при
возрастании численного значения
переменного вводимого фактора производства
с 6,2 до 9 единиц численные значения,
как предельного продукта, так и среднего
выпуска продукции уменьшаются (убывают),
оставаясь положительными. Однако
при этом функция общего выпуска продукции
продолжает возрастать до тех пор, пока
она не достигнет своего максимального
значения 9 единиц. В этой точке
величина функции предельного продукта,
MPХ=0. Эта стадия с точки
зрения оптимизации производственного
процесса является рациональной,
поскольку в ее пределах достигается
относительно допустимая сбалансированность
переменных и постоянных факторов
производства.
Стадия 3. На этой стадии функция
предельного продукта становится
отрицательной и общий выпуск продукции
убывает.
 На этой стадии выпуск продукции
представляется совершенно нерациональным.
На этой стадии выпуск продукции
представляется совершенно нерациональным.
Эластичность производства
Из графика, представленного на рис.
1., также можно получить наглядное
представление о том, что означает термин
«эластичность производства». Под
эластичностью производства, обозначаемой
символом εР, понимается
отношение величины относительного
изменения общего выпуска продукции,
∆Q/Q, к относительному изменению
переменного вводимого фактора
производства, ∆Х/Х, Таким образом,
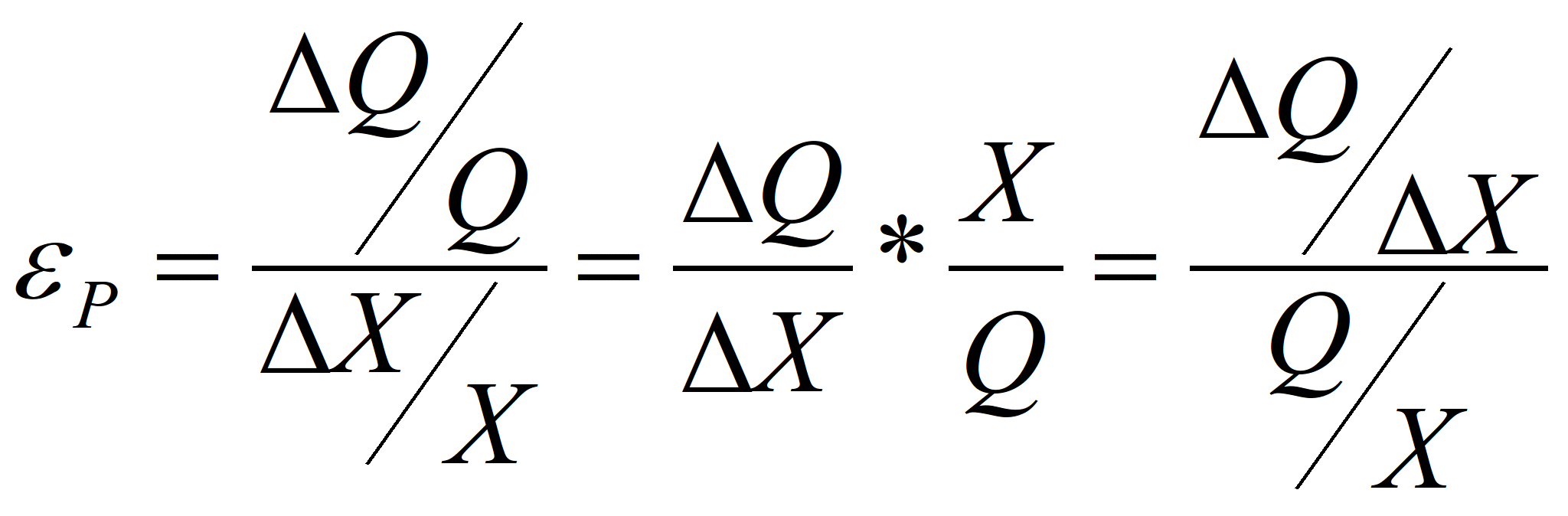 (4)
(4)
Поскольку ∆Q/∆X=MPХ
и Q/X=APХ, мы можем
преобразовать аналитическое выражение
для эластичности производства в
следующее:
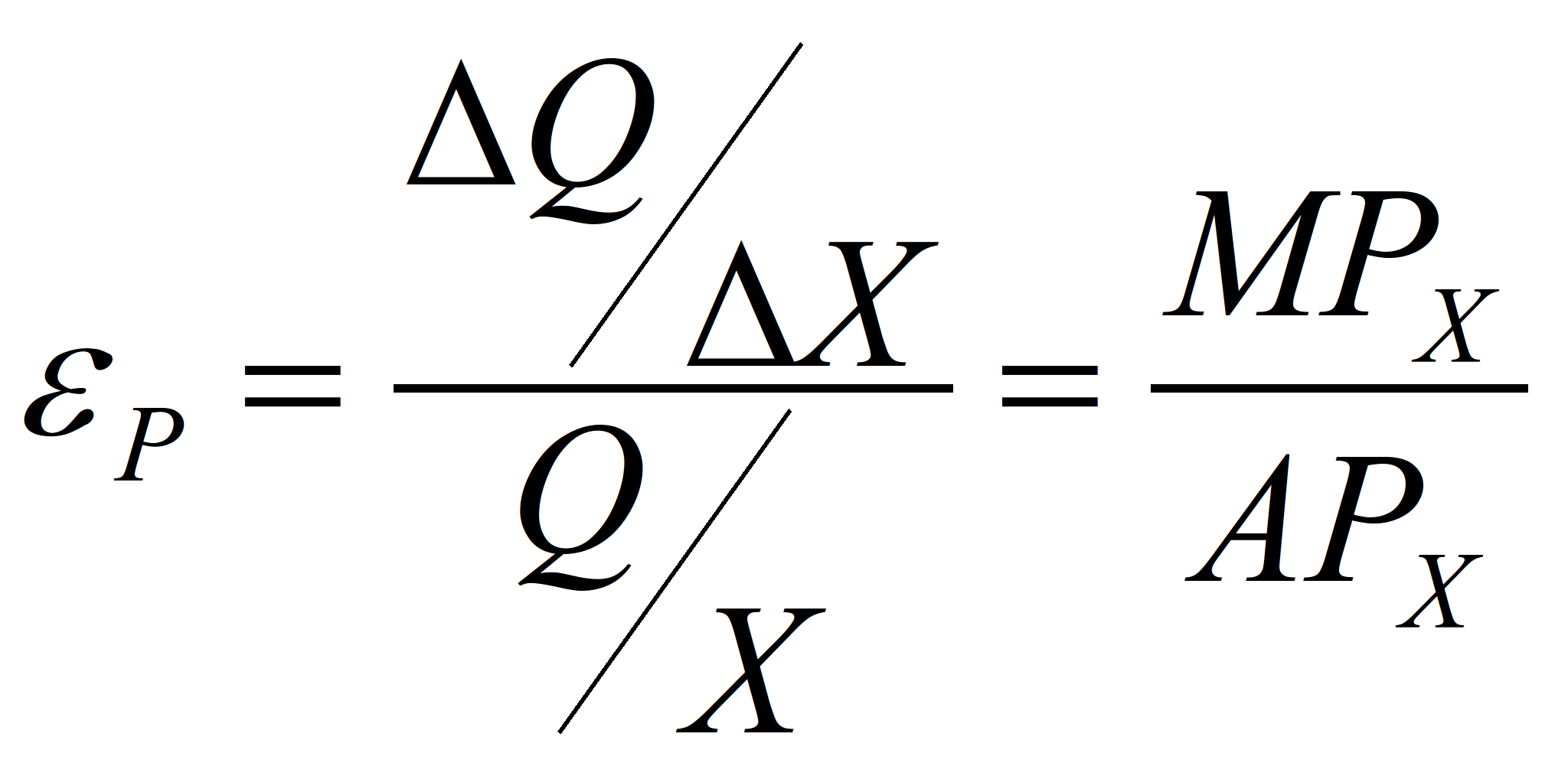 (5)
(5)
 Эластичность производства представляет
собой отношение предельного продукта
MPХ к среднему выпуску продукции
APХ , причем она является различной
в каждой точке кривой общего выпуска
продукции.
Эластичность производства представляет
собой отношение предельного продукта
MPХ к среднему выпуску продукции
APХ , причем она является различной
в каждой точке кривой общего выпуска
продукции.
Различные значения эластичности
производства εР,
представленные на рис. 1., и помогают
объяснить наличие трех стадий
производства.
В пределах стадии 1 коэффициент
эластичности больше единицы (εР>1),
поскольку MP>AP. Это означает,
что изменение величины переменного
вводимого фактора производства X на
1% приводит к изменению выпуска продукции
более, чем на 1%.
В начале стадии 2 имеет место
равенство MPХ=APХ,
и, следовательно, эластичность
производства εР=1. Это
означает, что изменение величины
переменного вводимого фактора производства
Х на 1% приводит к изменению выпуска
продукции также на 1%. В конце стадии
2 величина MP=0 и, следовательно,
εР=0. Это означает, что
при незначительном изменении величины
переменного вводимого фактора производства
Х не происходит никакого изменения
выпуска продукции.
При переходе к стадии 3 εР<0.
Это означает, что при изменении величины
переменного вводимого фактора производства
Х происходит снижение выпуска
продукции.
Производная предельного продукта
(MPХ'=dMPХ/dX).
Иногда нам необходимо определить, когда
MPХ достигает своего
максимума (точка перегиба) на рис. 1.
MPХ=max, при Х=4.
Аналитический анализ кривых
Аналитический метод анализа
производственной функции является
самым точным.
|
Таблица 2. |
|
№ варианта |
Исходные данные |
Ответ |
|
Q |
Xmax1 |
Xmax2 |
Точка перегиба |
|
1 |
2 |
3 |
4 |
|
1 |
Q = -79X^3 + 945X^2+1011X+850 |
-0,503 |
8,478 |
3,987 |
|
2 |
Q = -80X^3 + 955X^2+957X+822 |
-0,537 |
8,431 |
3,979 |
|
3 |
Q = -79X^3 + 946X^2+989X+872 |
-0,562 |
8,475 |
3,992 |
|
4 |
Q = -82X^3 + 981X^2+972X+840 |
-0,531 |
8,444 |
3,988 |
|
5 |
Q = -79X^3 + 917X^2+1006X+805 |
-0,594 |
8,253 |
3,869 |
|
6 |
Q = -81X^3 + 944X^2+900X+847 |
-0,510 |
8,220 |
3,885 |
|
7 |
Q = -81X^3 + 940X^2+1006X+853 |
-0,578 |
8,239 |
3,868 |
|
8 |
Q = -82X^3 + 913X^2+1014X+809 |
-0,605 |
7,942 |
3,711 |
|
9 |
Q = -79X^3 + 992X^2+987X+856 |
-0,531 |
8,842 |
4,186 |
|
10 |
Q = -75X^3 + 949X^2+1018X+813 |
-0,576 |
8,942 |
4,218 |
Ранее мы отмечали, что, изучив кривую
общего выпуска продукции, TPX=Q=f(X)
исследователи установили, что ее лучше
всего описать кубическим уравнением:
Q=a+bX+cX2+dX3=
=850+1011X+945X2-79X3
(колонка 1).
Аналитическое уравнение предельного
продукта MPХ будет иметь
вид:
MPХ=dQ/dX= b+2cX+3dX2=
=1011+1890X-237X2
Для того чтобы определить, сколько
максимально необходимо внести удобрений,
чтобы достигнуть максимального уровня
урожая картофеля, достаточно приравнять
уравнение MPХ=0 и решить
его относительно Х:
MPХ=dQ/dX= b+2cX+3dX2=
=1011+1890X-237X2=0
Решим полученное уравнение относительно
Х с помощью общей формулы для
корней квадратного уравнения:
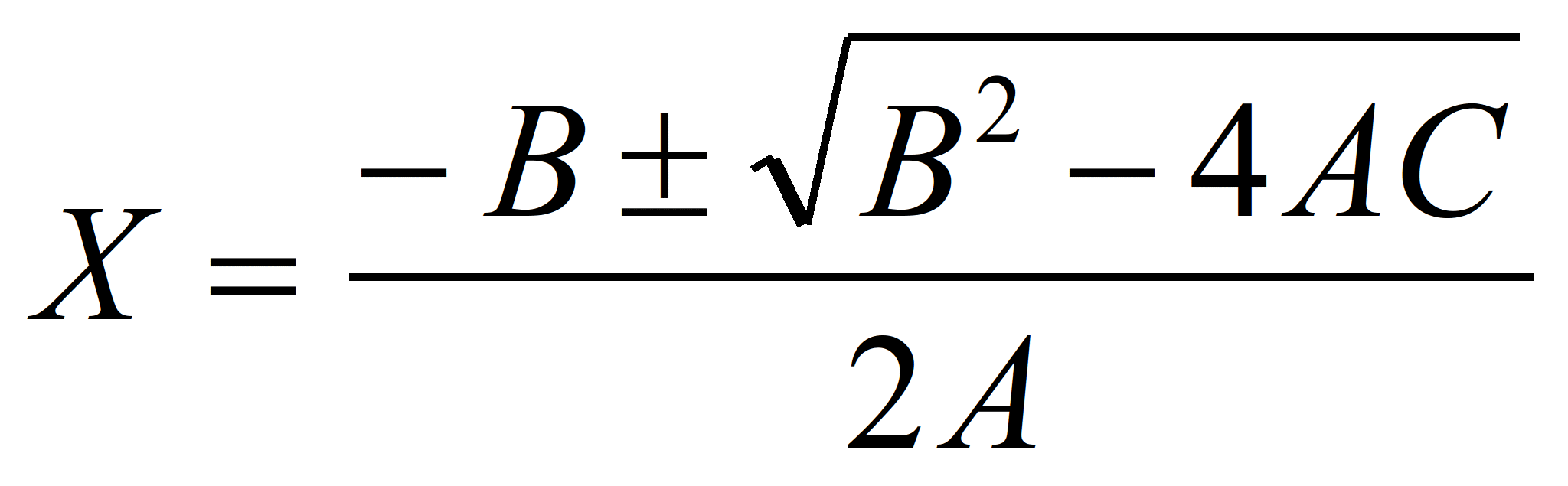
т.е. А=3d, В=2с и С=b. При MPХ=0
(т.е. при таком значении вводимого фактора
Х, когда уровень выпуска продукции
максимален), на рис. 1. это наглядно видно
– график функции MPХ пересекает
ось абсцисс.
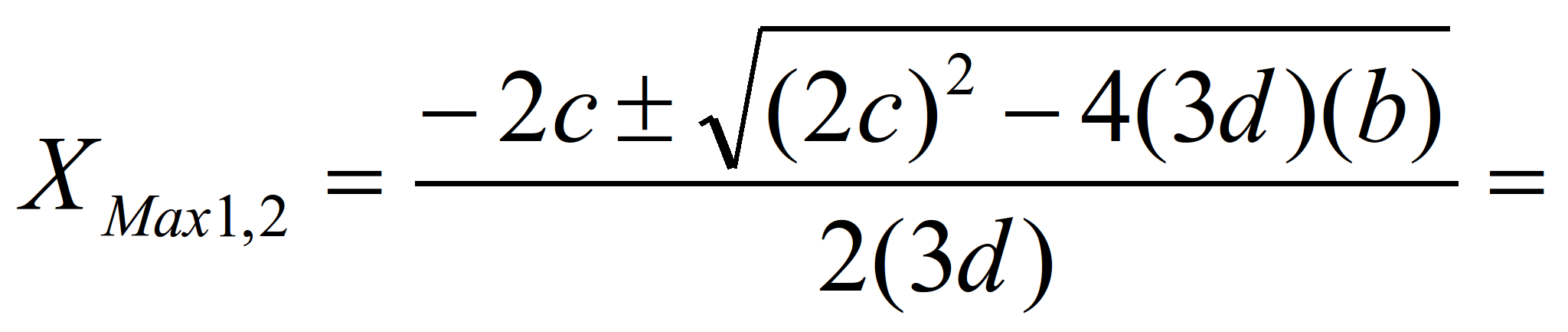 -0,503
или 8,478 (см. колонка 2, 3)
-0,503
или 8,478 (см. колонка 2, 3)
Поскольку отрицательное значение
вводимого фактора производства физически
невозможно, единственно возможный
ответ таков: для достижения максимального
уровня выпуска картофеля уровень
вводимого фактора производства X
должен быть равен 8,478 мешков удобрений.
Обратите внимания на рис. 1. при MPХ=0,
Х=9, т.е. и графический и табличный
методы грешат неточностью в отличие от
аналитического метода.
Аналитическое уравнение первой
производной предельного продукта
MPХ будет иметь вид:
MPХ'=dMPХ/dX=
2c+6dX= 1890-474X
Для того, чтобы определить значение,
при котором MPХ=max,
достаточно приравнять MPХ'=0:
MPХ'=dMPХ/dX=2c+6dX=
1890-474X=0
X=1890/474=3.987 (см. колонка 4)
Обратите внимания на рис. 1. при MPХ=max,
Х=4.
Мы сделали табличный, графический и
аналитический анализ производственной
функции. И теперь можем перейти к заданию.
В приведенной таблице 2. выберете свой
вариант. Постройте таблицу 1., графики
кривых, как показано на рис. 1., проведите
вычисления со своими данными и полученные
результаты сравните с ответами.
Ответьте на вопросы:
- Какие выводы можно сделать на основании
анализа этих кривых?
В чем заключаются важнейшие свойства
производственной функции?
Кубическая производственная функция
хорошо отражает как увеличивающуюся,
так и уменьшающуюся предельную
производительность, имеющую место, при
единственном переменном вводимом
факторе производства.
Если специфический вводимый фактор
производства отсутствует, то никакой
продукции выработано быть не может и,
следовательно, постоянный параметр
а будет равен нулю. В таком случае
кубическая производственная функция
обнаруживает следующие свойства.
Средний выпуск продукции. При
отсутствии в кубической функции параметра
а средний выпуск продукции APХ
для кубической производственной функции
может быть выражен в следующем виде:
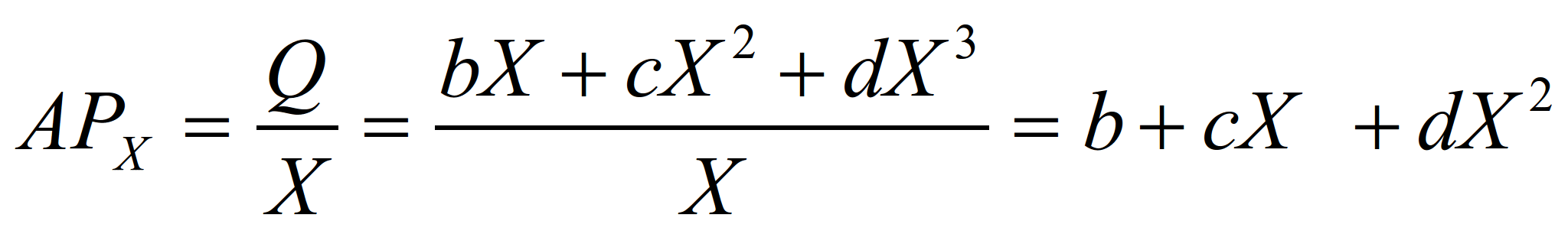 (6)
(6)
т.е. представляет собой квадратичную
функцию. Стадия 2 начинается в точке
пересечения кривых APХ и
MPХ, где величина
среднего выпуска продукции APХ
максимальна и равна величине
предельного продукта MPХ.
Предельный продукт также представляет
собой квадратичную функцию:
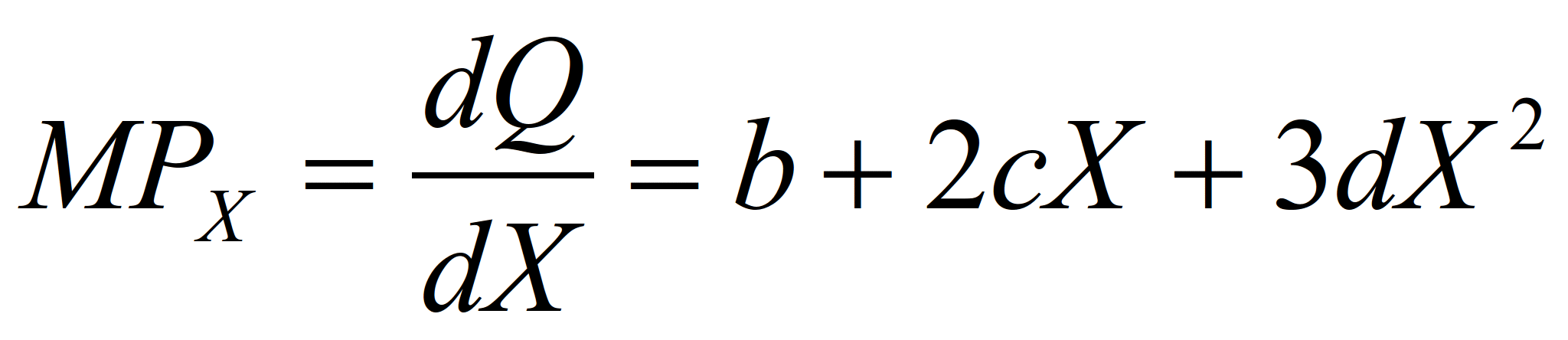 (7)
(7)
Поскольку параметр d в кубической
производственной функции всегда
отрицателен, предельный продукт
MPХ вначале увеличивается,
а затем уменьшается.
Эластичность. В отсутствие параметра
а эластичность производства может
быть выражена в виде:
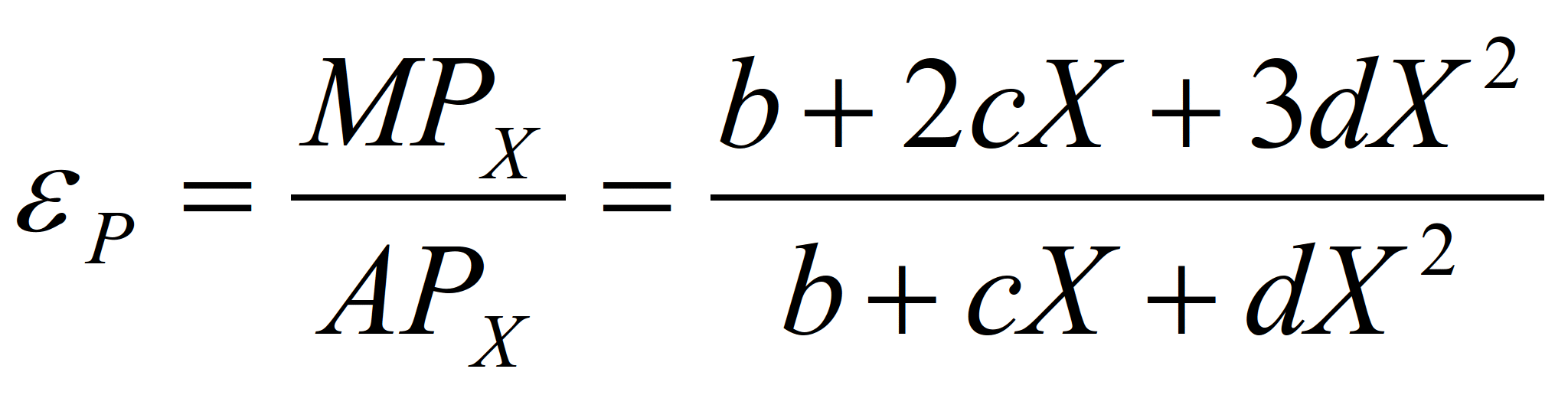 (8)
(8)
Поскольку указанное отношение
изменяется по величине при изменении
величины X, эластичность различна
в любой точке кривой общего выпуска
продукции.
Экономическая лаборатория. Равновесие
производства, минимизация издержек
Вами принято решение применить свои
знания и опыт в области коммерческой
д еятельности
для того, чтобы помочь одному из
предпринимателей наладить работу
обувной фабрики.
еятельности
для того, чтобы помочь одному из
предпринимателей наладить работу
обувной фабрики.
После изучения производственных
показателей фабрики за последние годы
ее работы вы собрали статистические
данные для построения зависимости
уровня выпуска обуви Q от количества
персонала, занятого в производстве, L.
Полученные точки вы нанесли на плоскость
Q0L. Как видно из рис. 2., размещение
реальных точек на плоскости может быть
хорошо описано (аппроксимировано,
приближено, подогнано) кубической
производственной функцией.
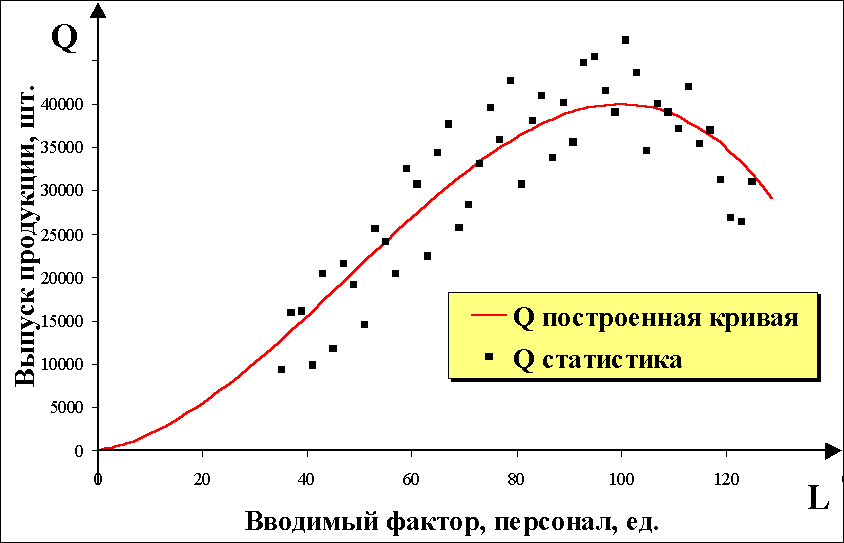
Рис. 2.Производственная
функция обувной фабрики Q=f(L)
При этом, когда дополнительный
вводимый фактор производства отсутствует,
то никакой продукции выработано быть
не может. Это очевидно, если производственный
персонал на фабрике отсутствует, т.е.
L=0 - некому производить обувь.
Следовательно, постоянный параметр a
будет равен нулю. В результате
производственная функция будет иметь
вид:
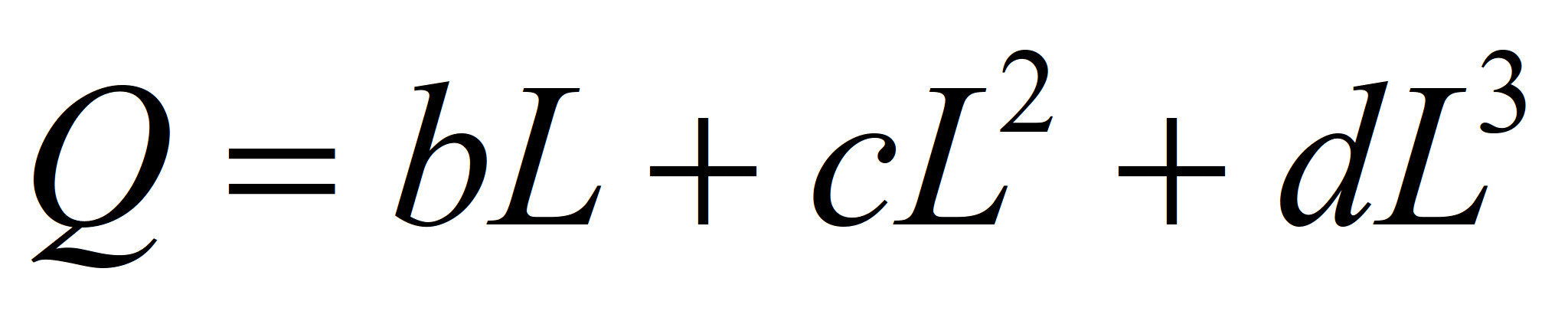 ,
,
т.к. a=0, то при условии L=0, функция
Q=0.
Далее, вручную с помощью лекал, линейки
(spline) и подбора коэффициентов b, c, d,
или с помощью стандартного программного
обеспечения (метода наименьших квадратов)
вы сможете построить производственную
функцию предприятия, как это показано
на рис. 2.
Когда производственная функция
построена, перед нами традиционно встают
вопросы:
- Какое количество рабочих L
необходимо иметь на фабрике для
обеспечения максимальной эффективности
производства?
-
Какое количество пар обуви в месяц
будет производить фабрика при условии
максимальной эффективности производства?
-
Какую среднюю месячную норму
установить для одного рабочего?
Сколько максимально необходимо
рабочих, чтобы на имеющихся
производственных площадях, технологическом
оборудовании и с данной технологией
производства обуви достичь максимального
уровня выпуска продукции (пар обуви)
в месяц?
Исходные данные возьмем из таблицы
3. для варианта 1.
Q=100L+10L2-0,07L3
(9) (см. колонка 1)
где Q - уровень выпуска обуви в
месяц; L - количество рабочих
(производственный персонал).
Для того, чтобы определить, какое
количество рабочих L необходимо
иметь на фабрике для обеспечения
максимальной эффективности производства,
давайте, определим, что такое максимальная
эффективность производственной
функции.
Максимальная эффективность
производства имеет место, когда
величина среднего выпуска продукции
APХ максимальна. Этому
условию соответствует точка, в которой
APХ=MPХ (см.
рис. 3.), т.е. когда:
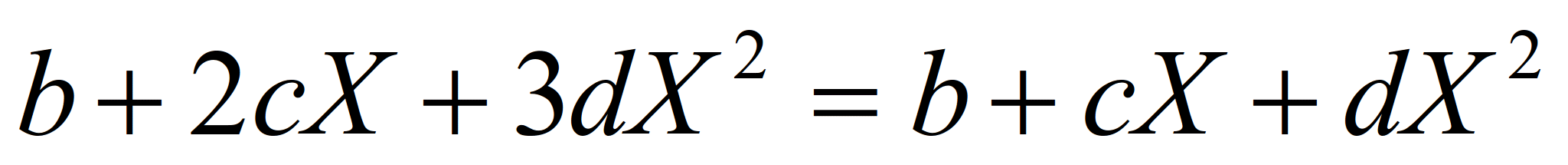
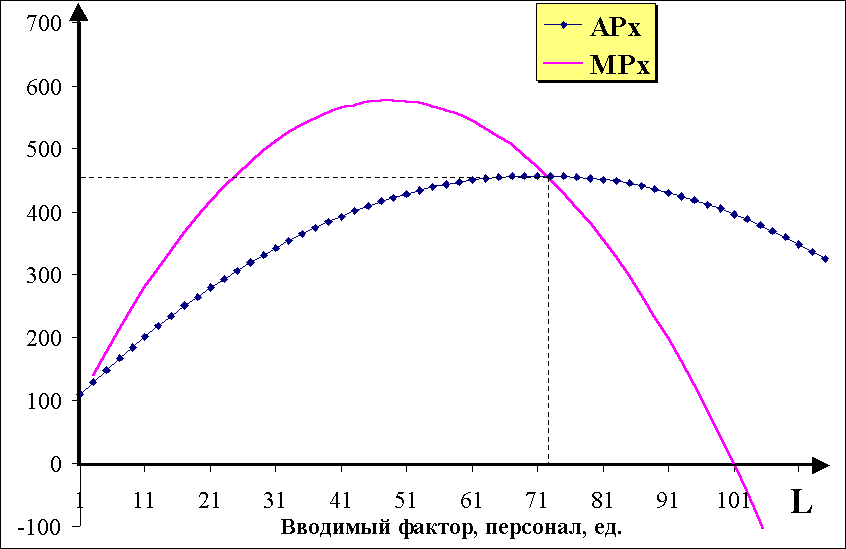
Рис. 3.Соотношения
среднего выпуска продукции APL
и предельного продукта MPL
Группируя подобные члены, получим:
cX+2dX2=0
Вынося общий множитель за скобки,
получим выражение:
X(c+2dX)=0
Следовательно, величина X имеет
два возможных значения:
X=0 и X=-c/2d (10)
Второе решение указывает, какое
количество вводимого фактора производства
X следует ввести в технологический
процесс, чтобы вводимые ресурсы
использовались наиболее эффективно. В
нашем случае вводимый фактор X=L-
количество рабочих.
L=-c/2d=-10/(2*(-0,07))= 71.429≈71 производственных
рабочих. (см. колонка 2)
Округление необходимо, т.к. 0,429
рабочего работать явно не сможет.
При указанном значении вводимого
фактора уровень выпуска продукции
составил бы:
Q=100(71)+10(71)2-0.07(71)3
≈32 456 пар обуви в месяц. (см. колонка
3).
Средняя месячная норма на одного
работника составила бы:
APL=Q/L=32456/71≈457 пар
обуви на одного работника в месяц.
Или
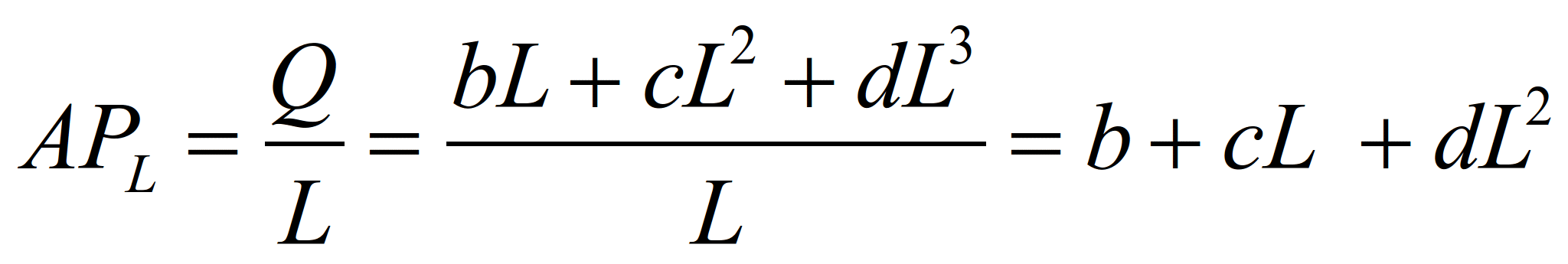
APL=b+cL+dL2=100+10(71)-0.07(71)2≈457
(см. колонка 4)
Предельный продукт может быть вычислен
по формуле:
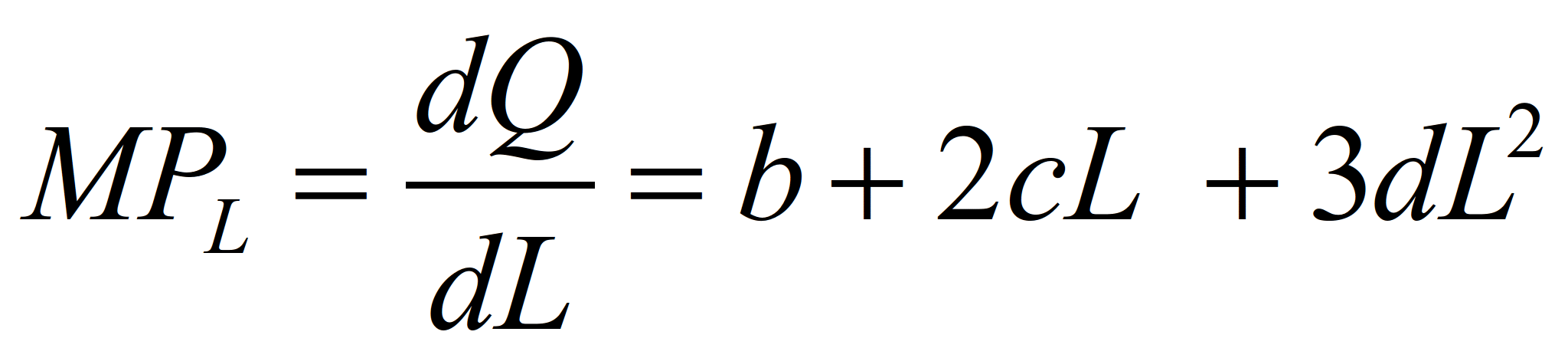
MPL=100+2(10)(71)+3(-0,07)
(71)2≈461 (см. колонка 5)
MPL численно должен быть
равен среднему выпуску продукции APL
при указанном значении вводимого фактора
производства L, но на самом деле это
равенство не наблюдается.
 Причина этого - округление полученных
значений. Количество производственного
персонала, количество пар обуви не может
быть выражено дробным числом.
Причина этого - округление полученных
значений. Количество производственного
персонала, количество пар обуви не может
быть выражено дробным числом.
Ответим на последний вопрос -
сколько максимально необходимо
привлечь производственного персонала,
чтобы на имеющихся производственных
площадях, технологическом оборудовании
и с данной технологией производства
обуви достичь максимального уровня
выпуска продукции (пар обуви) в месяц?
Чтобы найти указанный уровень вводимого
фактора L, представим функцию
предельного продукта в обычном виде,
приравняем ее нулю:
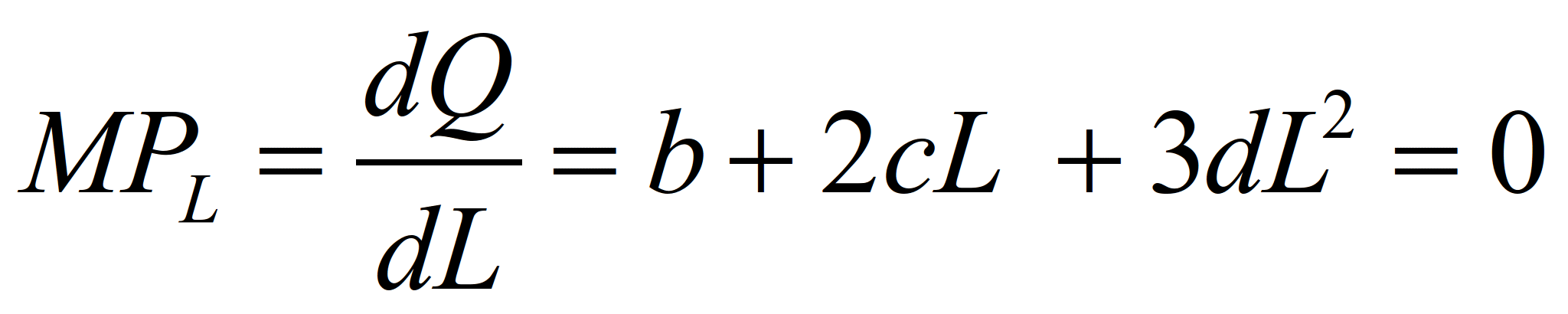
Решим полученное уравнение относительно
L с помощью общей формулы для
корней квадратного уравнения:
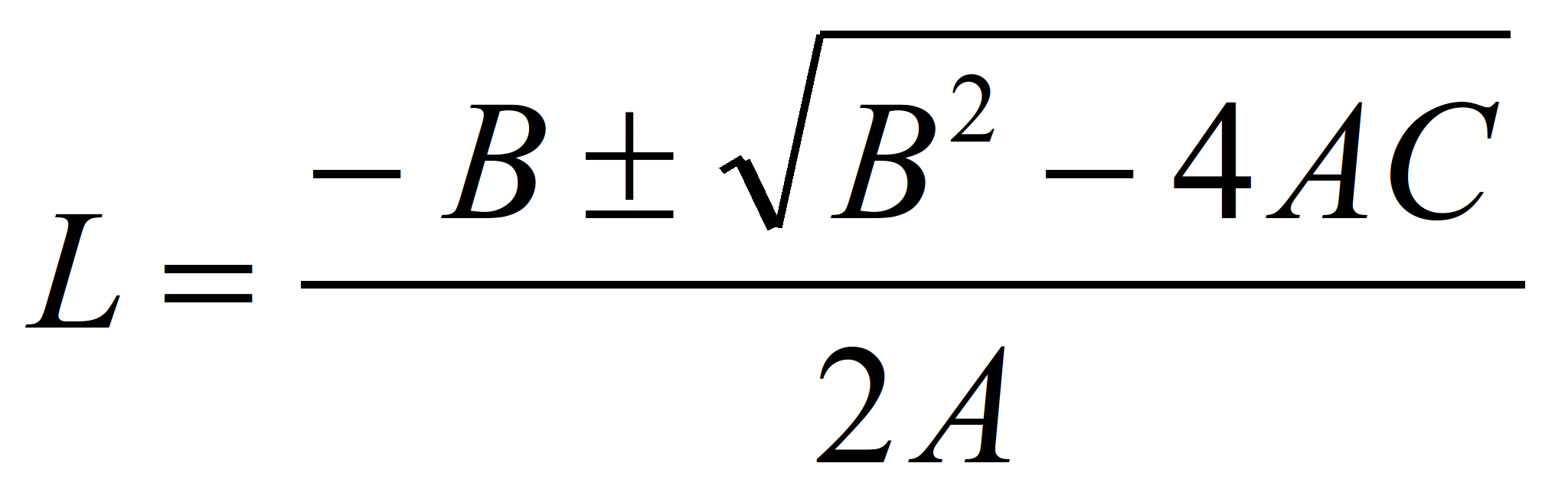 (11)
(11)
т.е. А=3d, В=2с и С=b. При MPL=0
(т.е. при таком значении вводимого фактора
L, когда уровень выпуска продукции
максимален), на рисунке это наглядно
видно – график функции MPL
пересекает ось абсцисс.
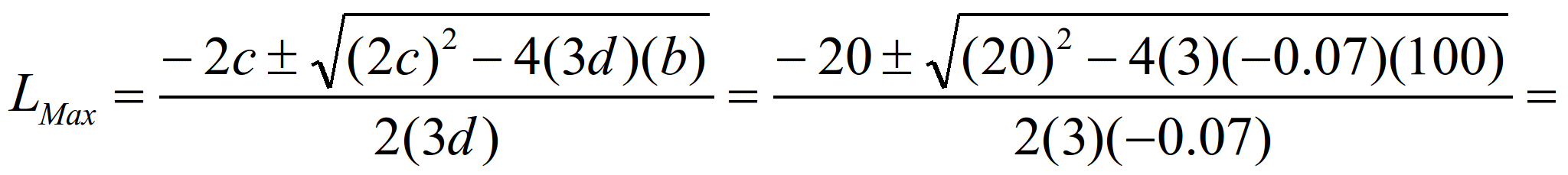 -4,7619
или 100 (см. колонка 6 и рис. 2)
-4,7619
или 100 (см. колонка 6 и рис. 2)
Поскольку отрицательное значение
вводимого фактора производства физически
невозможно, единственно возможный ответ
таков: для достижения максимального
уровня выпуска продукции уровень
вводимого фактора производства L
должен быть равен 100 рабочим.
При указанном значении вводимого
фактора уровень выпуска продукции
составил бы:
Qmax=100(100)+10(100)2-0.07(100)3
≈ 40 000 пар обуви в месяц. (см. колонка
7)
В приведенной таблице 3. выберете свой
вариант. Проведите вычисления и полученные
результаты сравните с ответами.
-
|
Таблица 3. |
|
№ |
Исходные данные |
Ответ |
|
Q=bL+cL2+dL3 |
L |
Q |
АРL |
MPL |
Lmax |
Qmax |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1 |
Q=100L+10 L2-0,07L3 |
71 |
32456 |
457 |
461 |
100 |
40000 |
|
2 |
Q=144L+13 L2-0,02L3 |
325 |
733363 |
2257 |
2257 |
439 |
876499 |
|
3 |
Q=64L+18 L2-0,04L3 |
225 |
470025 |
2089 |
2089 |
302 |
559256 |
|
4 |
Q=156L+23 L2-0,04L3 |
288 |
997125 |
3462 |
3451 |
387 |
1186635 |
|
5 |
Q=88L+10 L2-0,09L3 |
56 |
20483 |
366 |
361 |
78 |
24994 |
|
6 |
Q=85L+26 L2-0,01L3 |
1300 |
22080500 |
16985 |
16985 |
1735 |
26185921 |
|
7 |
Q=92L+10 L2-0,02L3 |
250 |
335500 |
1342 |
1342 |
338 |
401247 |
|
8 |
Q=130L+10 L2-0,01L3 |
500 |
1315000 |
2630 |
2630 |
673 |
1568568 |
|
9 |
Q=67L+21 L2-0,02L3 |
525 |
2929238 |
5580 |
5580 |
702 |
3476950 |
|
10 |
Q=74L+18 L2-0,06L3 |
150 |
213600 |
1424 |
1424 |
202 |
254876 |
При обсуждении характерных особенностей
взаимозависимости предельного продукта
и среднего выпуска продукции было
отмечено, что хотя, согласно графику,
представленному на рис. 1., максимальная
эффективность достигается в точке,
соответствующей началу стадии 2, где
справедливо равенство MPХ=APХ,
это отнюдь не означает, что указанная
точка обязательно соответствует
получению максимальной прибыли.
Точная оценка суммы затрат на переменный
вводимый фактор производства, которая
необходима для получения максимальной
прибыли, будет зависеть от цены
переменного фактора, величины
предельного продукта при данном
значении переменного вводимого фактора
и продажной цены выпускаемой продукции.
Для того, чтобы установить на основе
анализа наиболее рентабельный уровень
производства, необходимо познакомиться
со смысловым содержанием и аналитическим
выражением таких терминов (понятий),
как предельный (добавочный) доход,
предельные (приростные) издержки,
предельный продукт в натуральном
выражении, предельный продукт в денежной
форме.
Предельный доход, обозначаемый
здесь и далее MRQ,
представляет собой дополнительный
(добавочный) доход, получаемый в
результате продажи одной дополнительной
единицы продукции:
MRQ =∆TR/∆Q (12)
Если цена единицы продукции
неизменна, то в таком случае предельный
доход просто представляет собой цену
единицы продукции.
Предельные (приростные) издержки,
обозначаемые здесь и далее как MCQ,
представляют собой дополнительные
издержки при увеличении объема
производства на одну дополнительную
единицу продукции. Эта величина позволяет
определить темп (скорость) изменения
общих издержек производства при
изменении объема производства с
помощью следующего выражения:
MCQ =∆TC/∆Q (13)
Предельный продукт, обозначаемый
здесь и далее как MPХ,
представляет собой дополнительное
количество продукции, получаемой в
результате использования одной
дополнительной единицы переменного
вводимого фактора производства:
MPX =∆TP/∆X (14)
Предельный продукт в денежной форме
как функция вводимого фактора Х,
обозначаемый здесь и далее как MRPХ,
представляет собой дополнительный
доход, получаемый в результате
использования одной дополнительной
единицы переменного вводимого фактора
производства X. Другими словами,
это экономически выгодное значение
одной единицы переменного вводимого
фактора производства. Количественно
оно может быть вычислено как произведение
предельного дохода на величину предельного
продукта, получаемого при введении в
производство единицы переменного
фактора. Аналитически это может быть
представлено в виде уравнения:
MRPX=MRQMPX
(15)
Например, предположим, что дополнительный
выпуск продукции при затратах труда в
течение часа (MPL)
равен 50 единицам и продукция реализуется
по цене 0,5 долл. за единицу (MRQ).
Тогда
MRPL=0,5 долл.*50 ед.=25 долл.
Иными словами, каждый дополнительный
(добавочный) час труда приносит 25 долл.
дохода.
Если дополнительные издержки на оплату
труда составляют менее 25 долл. в час, то
в таком случае фирма может получать
дополнительный доход и дополнительную
прибыль за счет привлечения дополнительной
рабочей силы вплоть до такого значения,
которое соответствует точке. В данной
точке предельный продукт в денежной
форме от дополнительного труда численно
равен цене или величине издержек на
оплату труда. Другими словами, прибыль
будет максимальной, если соблюдается
условие
MRPL= MRQ MPL=PL
(16)
Уравнение (16) справедливо для любого
переменного вводимого фактора
производства. Следовательно, в общем
виде мы имеем:
MRPX= MRQ MPX=PX
(17)
Производственная функция c эффективной
зарплатой
Пусть производится один продукт и при
этом используется единственный ресурс
- труд. Если выпуск зависит не только от
численности персонала фирмы, но и от
ставки зарплаты, то он представляет
собой производственную функцию c
эффективной зарплатой:
P=P(L,w),
где L - численность персонала, w
- ставка зарплаты.
Предельным продуктом зарплаты
называют прирост выпуска, полученный
в результате увеличения ставки зарплаты
на единицу при постоянной численности
персонала.
Предполагается, что предельный
продукт зарплаты не возрастает.
Задание 1. Производственная функция
P = (Lw)0,5.
Цена продукта равна 23, численность
персонала - 42.
Найти ставку зарплаты, при которой
прибыль максимальна.
Решение:
1. Выручка равна: 23•420.5w0,5.
2. Затраты равны количество персонала
умноженного на среднюю заработную
плату: 42w
3. Прибыль равна выручка минус затраты:
Pr=23•420.5w0,5-42w
4. Дифференцируем выражение для
прибыли по заработной плате и приравниваем
его нулю, получаем:
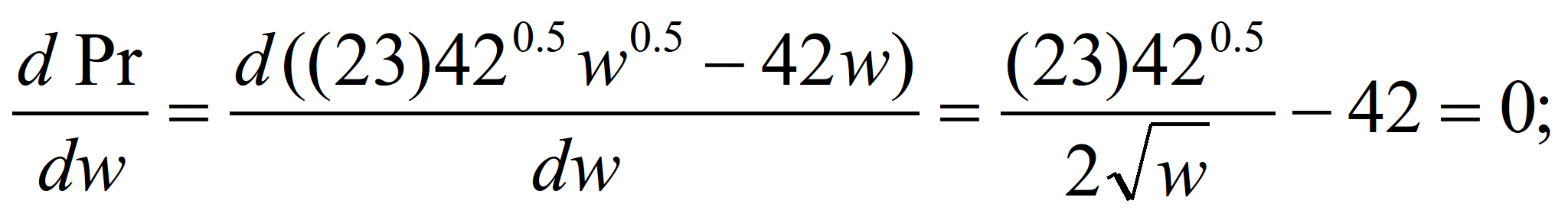
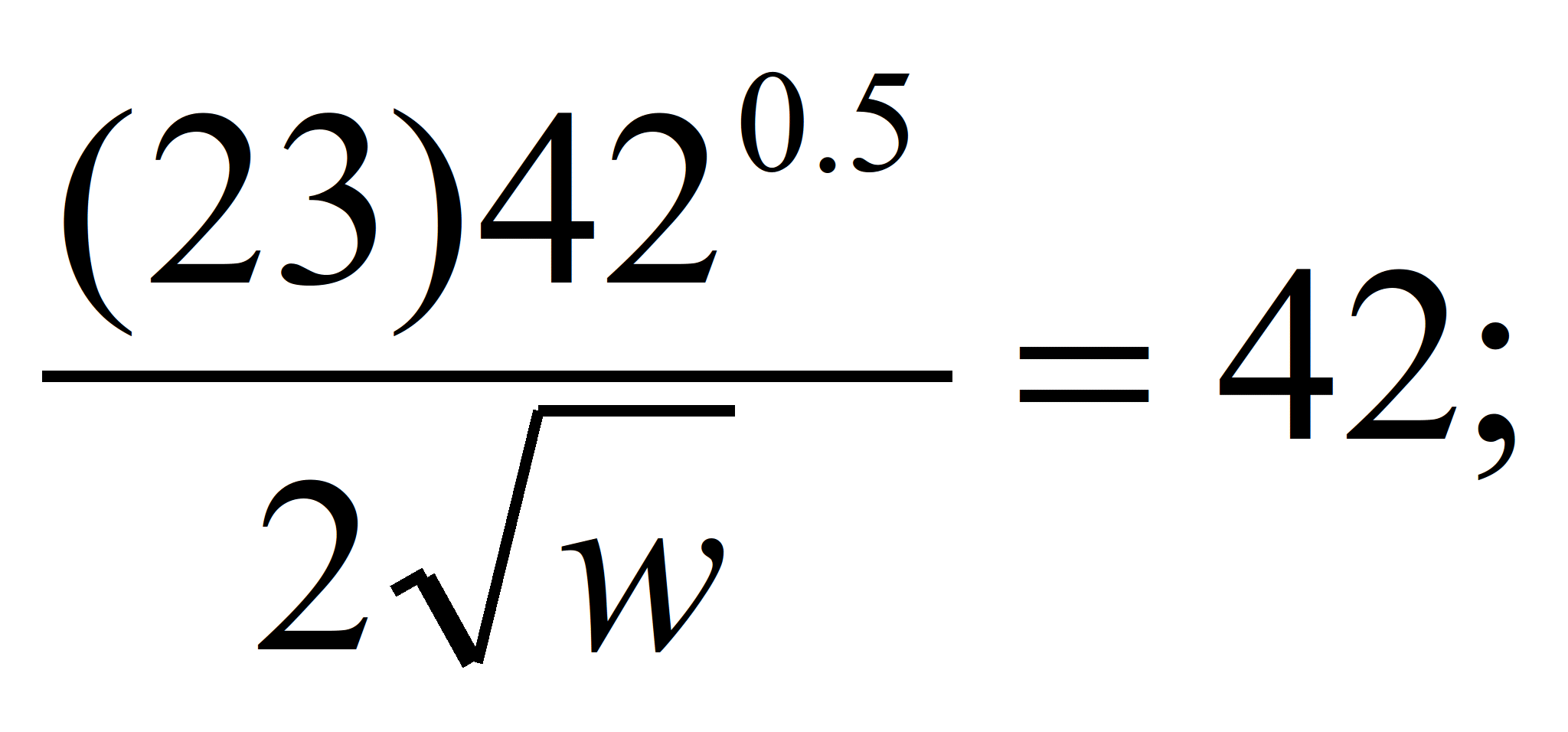
5. Ставка зарплаты, при которой прибыль
максимальна:
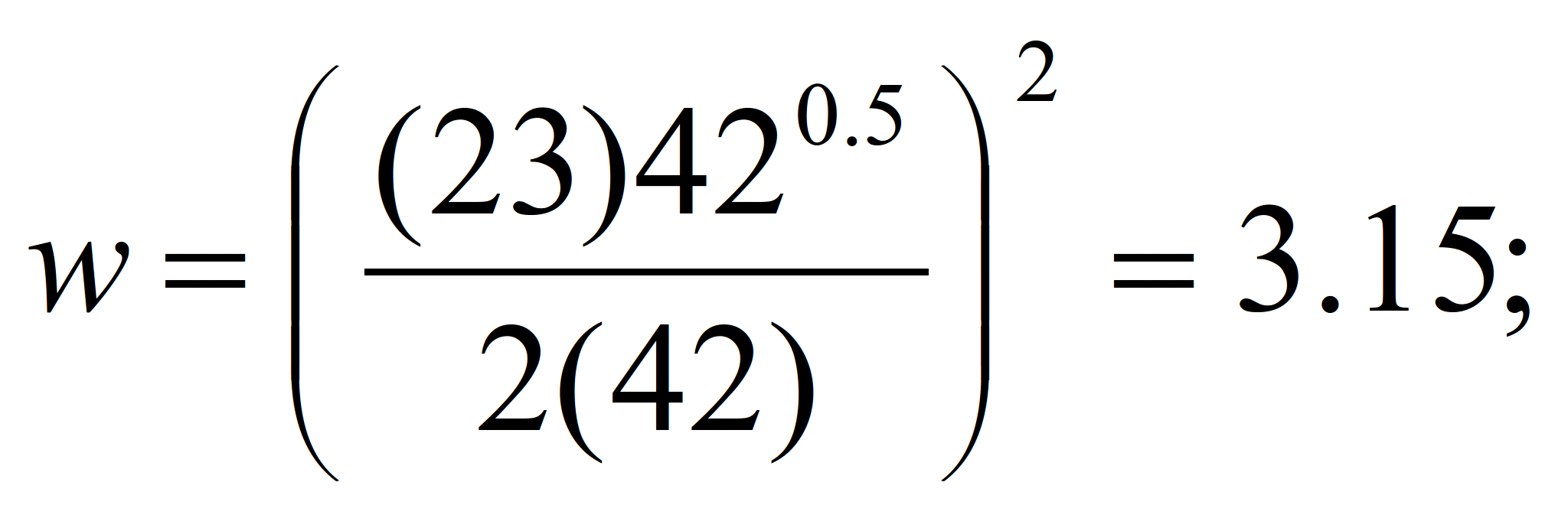
Задание 2. Производственная функция
P=Lw0,5. Цена продукта равна
8:
а) Найти ставку зарплаты, которая
обеспечивает максимум прибыли при
неизвестной численности персонала.
б) Найти максимальную прибыль, если
численность персонала - 28.
Решение:
а) Найдем ставку зарплаты, которая
обеспечивает максимум прибыли при
неизвестной численности персонала.
1. Выручка равна: 10•Lw0,5.
2. Затраты равны количество персонала
умноженного на среднюю заработную
плату: Lw
3. Прибыль равна выручка минус затраты:
Pr=10•Lw0,5- Lw
4. Дифференцируем выражение для
прибыли по заработной плате и приравниваем
его нулю, получаем:
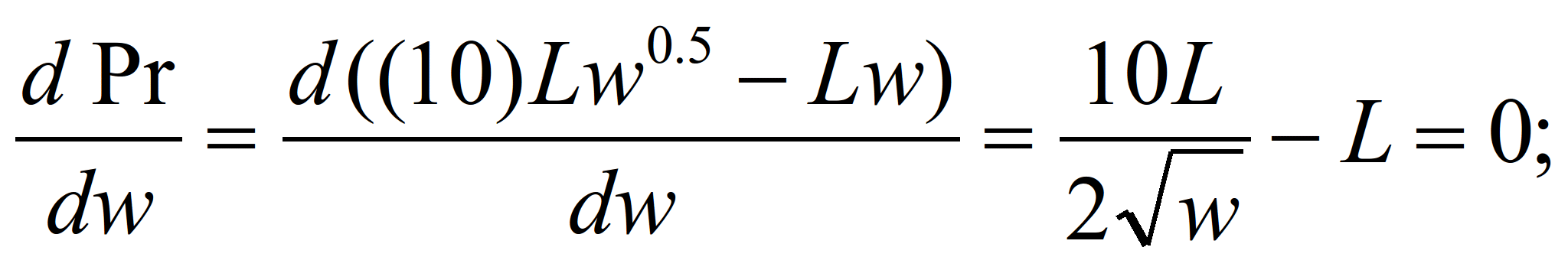
5. Ставка зарплаты, при которой прибыль
максимальна:
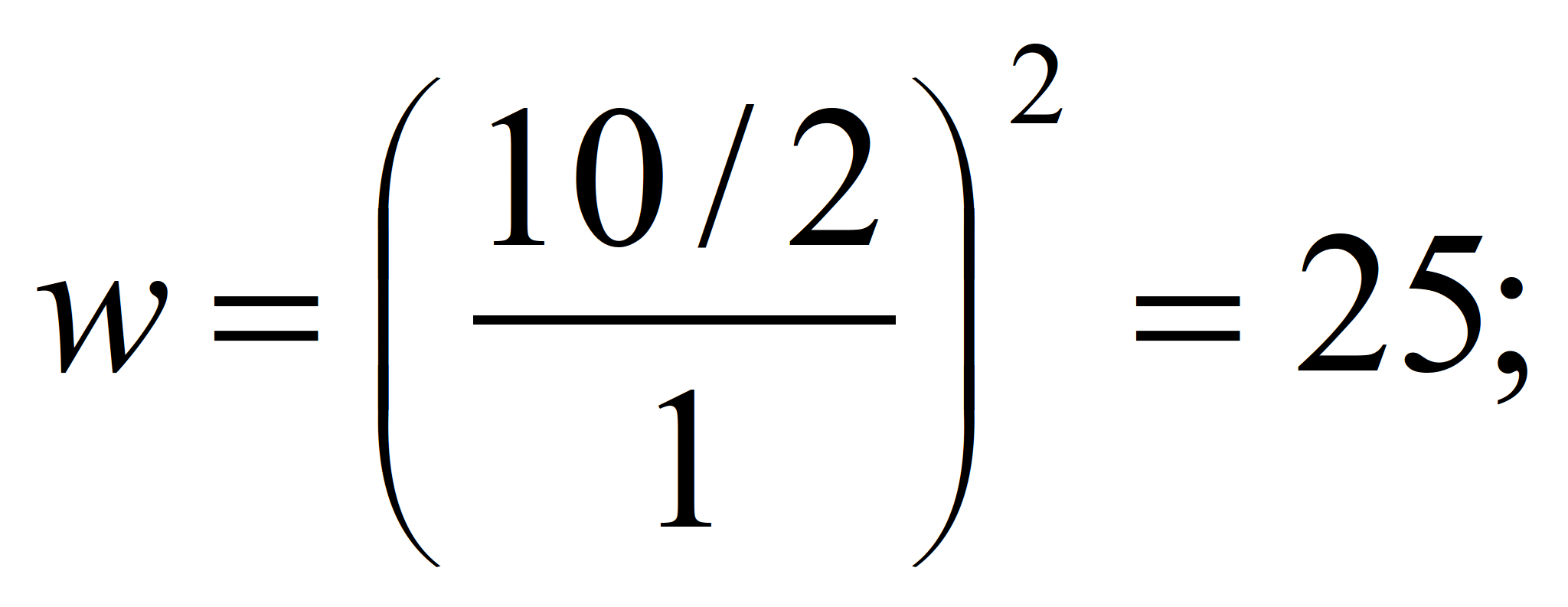
б) Найти максимальную прибыль, если
численность персонала - 28.
1. Выручка равна: 10•28w0,5.
2. Затраты равны количество персонала
умноженного на среднюю заработную
плату: 28w
3. Прибыль равна выручка минус затраты:
Pr=10•28w0,5- 28w
4. Дифференцируем выражение для
прибыли по заработной плате и приравниваем
его нулю, получаем:
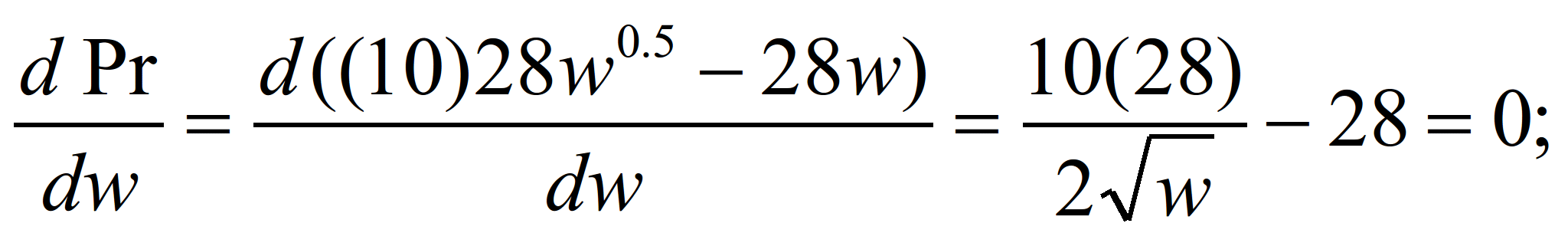
5. Ставка зарплаты, при которой прибыль
максимальна:
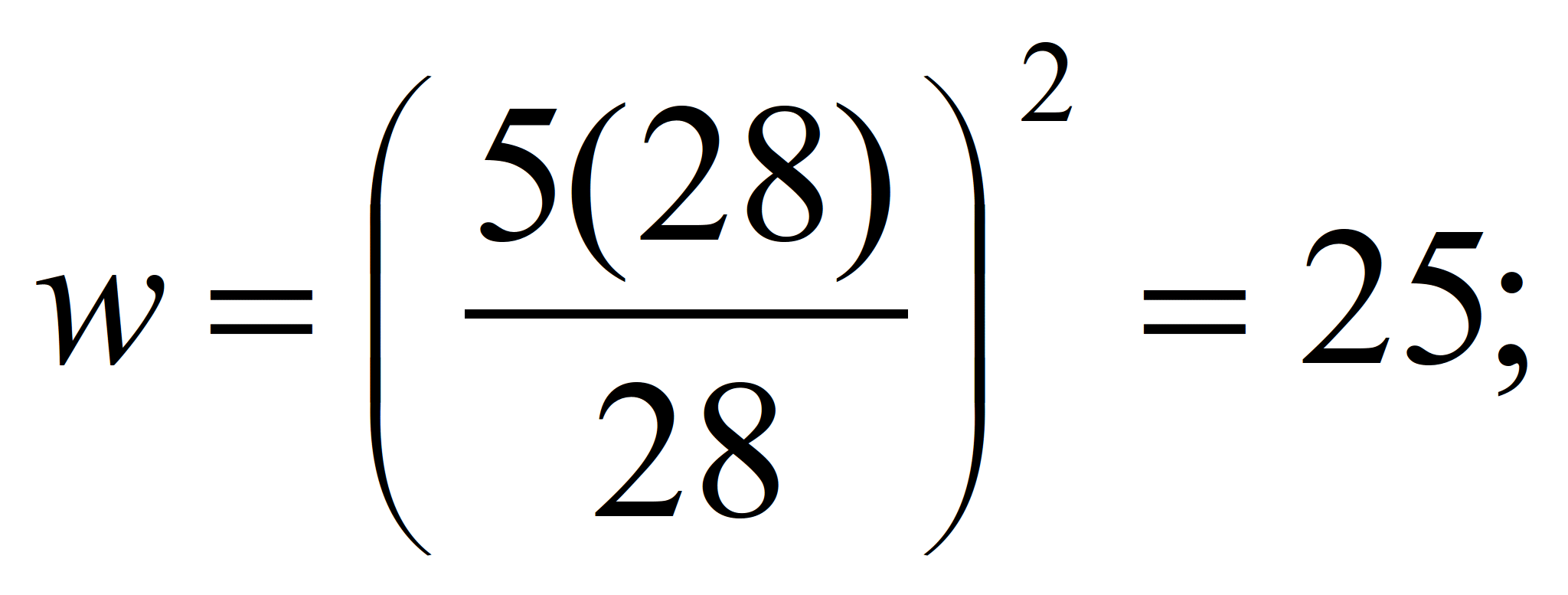
6. Максимальная прибыль составит:
Pr=10•28(25)0,5- 28(25)=700
Задание 3. Производственная функция
P = (Lw)0,5. Цена продукта
равна 8.
а) При каких издержках производителя
прибыль максимальна?
б) Найти максимальную прибыль.
Решение:
а) Найдем издержки производителя, при
которых прибыль максимальна.
1. Под издержками производителя будем
понимать его затраты на персонал, т.е.
Lw, приравняем издержки Х=Lw
2. Прибыль равна выручка минус затраты:
Pr=8(X)0,5-Х
3. Дифференцируем выражение для
прибыли по издержкам производителя и
приравниваем его нулю, получаем:
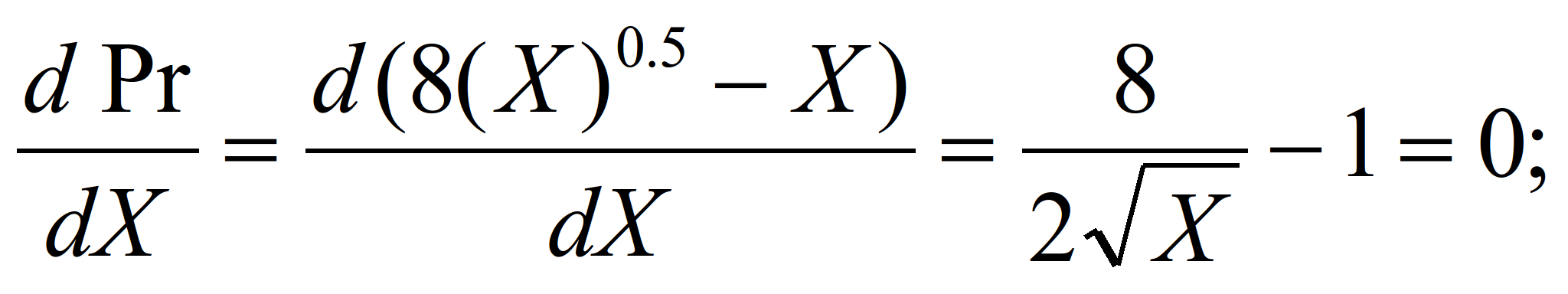
4. Издержки (затраты) производителя,
при которой прибыль максимальна:
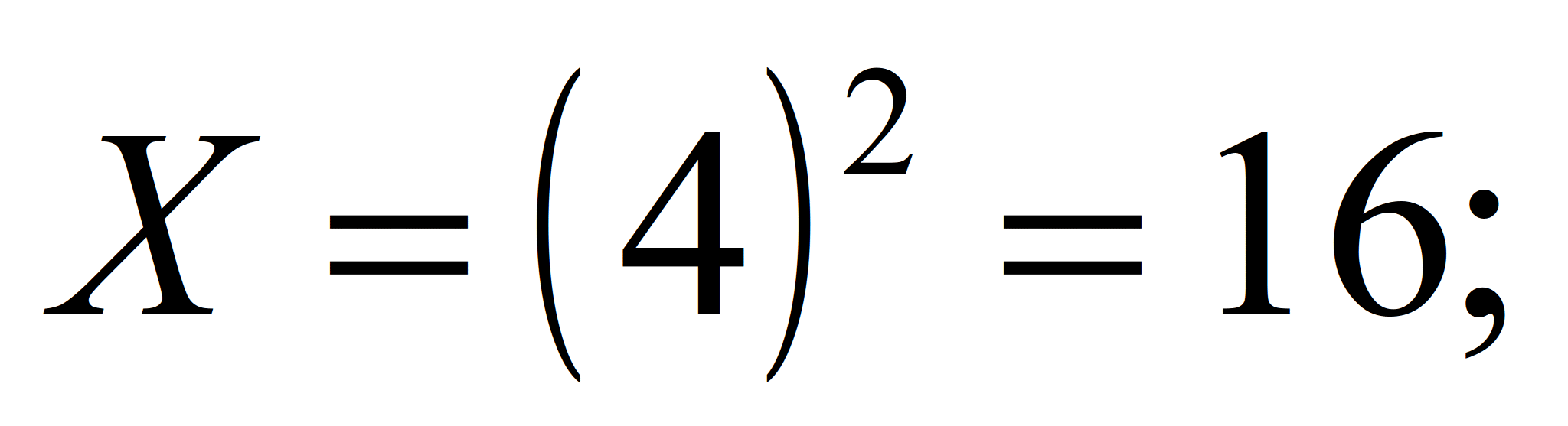
б) Найдем максимальную прибыль.
Максимальная прибыль составит:
Pr=8(X)0,5-Х=8(16)0,5-16=16
В приведенной таблице 4. выберете свой
вариант. Проведите вычисления и полученные
результаты сравните с ответами.
|
Таблица 4. |
|
№ Варианта |
Задание 1 |
Задание 2 |
Задание 3 |
|
Исходные данные |
Ответ |
Исходные данные |
Ответ |
Исходные данные |
Ответ |
|
P |
L |
w |
P |
L |
w |
w1 |
PrMax |
P |
Lw |
PrMax |
|
1 |
23 |
42 |
3,15 |
10 |
28 |
25 |
25 |
700 |
8 |
16 |
16 |
|
2 |
16 |
5 |
12,8 |
17 |
27 |
72,25 |
72,25 |
1950,8 |
20 |
100 |
100 |
|
3 |
7 |
14 |
0,88 |
17 |
35 |
72,25 |
72,25 |
2528,8 |
7 |
12,25 |
12,25 |
|
4 |
11 |
18 |
1,68 |
16 |
23 |
64 |
64 |
1472 |
16 |
64 |
64 |
|
5 |
18 |
46 |
1,76 |
18 |
10 |
81 |
81 |
810 |
8 |
16 |
16 |
|
6 |
14 |
38 |
1,29 |
20 |
13 |
100 |
100 |
1300 |
15 |
56,25 |
56,25 |
|
7 |
15 |
23 |
2,45 |
11 |
27 |
30,25 |
30,25 |
816,75 |
17 |
72,25 |
72,25 |
|
8 |
5 |
28 |
0,22 |
13 |
9 |
42,25 |
42,25 |
380,25 |
6 |
9 |
9 |
|
9 |
5 |
36 |
0,17 |
13 |
48 |
42,25 |
42,25 |
2028 |
15 |
56,25 |
56,25 |
|
10 |
18 |
43 |
1,88 |
8 |
40 |
16 |
16 |
640 |
20 |
100 |
100 |
Равновесие производства: оптимальное
сочетание нескольких переменных вводимых
факторов производства
 Комбинация переменных вводимых факторов
производства с наименьшими издержками
на единицу продукции достигается в том
случае, когда стоимость любого переменного
вводимого фактора суммируется с общим
выпуском продукции как стоимость любого
другого переменного вводимого фактора
производства в денежных единицах.
Комбинация переменных вводимых факторов
производства с наименьшими издержками
на единицу продукции достигается в том
случае, когда стоимость любого переменного
вводимого фактора суммируется с общим
выпуском продукции как стоимость любого
другого переменного вводимого фактора
производства в денежных единицах.
В соответствии со сказанным и если мы
примем, что MPА выражает
количество предельного продукта A,
a PA - цену предельного
продукта А, и воспользуемся
аналогичной символикой для прочих
вводимых факторов производства В,
С, ... , N, то в таком
случае уравнение минимальных издержек
может быть представлено в виде:
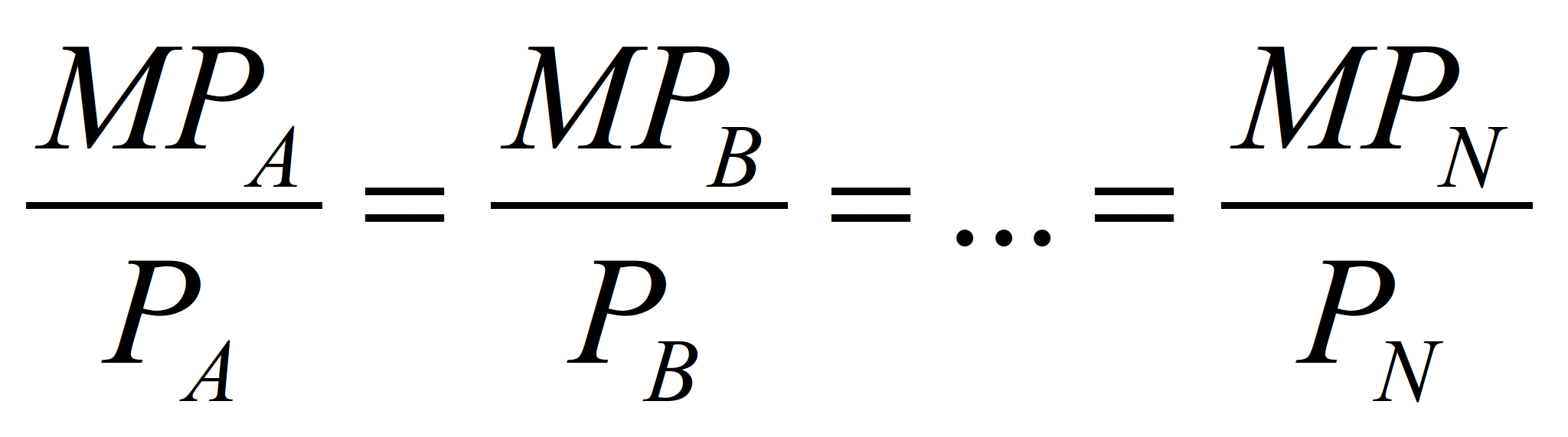 (18)
(18)
Это уравнение выражает правило
минимальных издержек. Вывод этого
уравнения аналогичен методу кривой
безразличия, применяемому при анализе
спроса. Предположим, что у нас имеются
два вводимых фактора производства, а
именно: труд (рабочая сила) L
(вместо A) и капитал С
(вместо В). Выполнив перекрестное
умножение, мы получим следующее выражение:
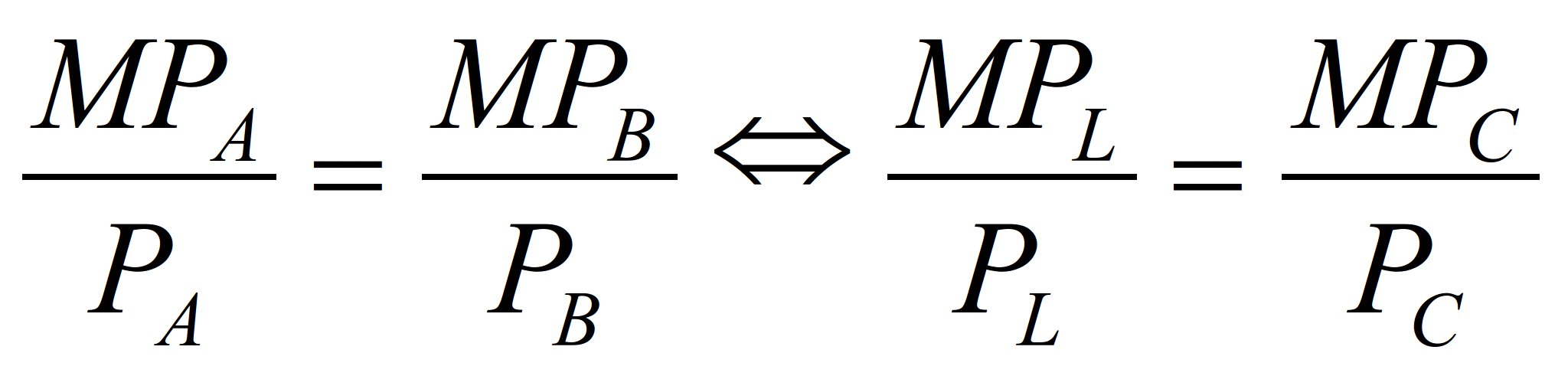 (19)
(19)
Это уравнение может быть легко
распространено на любое количество
вводимых факторов производства и, таким
образом, превращается в уравнение
минимальных издержек.
Экономическая лаборатория. Равновесие
производства, минимизация издержек.
Чтобы наглядно показать, как определяется
оптимальная комбинация вводимых факторов
производства, примем в качестве исходной
производственную функцию:
P=k Lβ1 Cβ2
(20)
Исходные данные возьмем из таблицы
5. для варианта 1. Коэффициент k=1,01
(колонка 1), привлеченный труд – L,
его коэффициент β1=0,75
(колонка 2), привлеченный капитал C,
его коэффициент β2=0,25
(колонка 3).
|
Таблица 5. |
|
№ |
Исходные данные |
Ответ |
|
k |
β1 |
β2 |
PL |
PC |
VС |
C/L |
L |
C |
P' |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
1,01 |
0,75 |
0,25 |
12 |
2 |
1000 |
2,00 |
62,5 |
125 |
75,0687 |
|
2 |
3,74 |
0,52 |
0,48 |
14 |
4 |
9095 |
3,23 |
338 |
1091 |
2218,28 |
|
3 |
4,22 |
0,54 |
0,46 |
19 |
1 |
1049 |
16,19 |
29,8 |
483 |
452,816 |
|
4 |
3,33 |
0,45 |
0,55 |
20 |
3 |
3565 |
8,15 |
80,2 |
654 |
846,776 |
|
5 |
4,46 |
0,34 |
0,66 |
15 |
1 |
3344 |
29,12 |
75,8 |
2207 |
3128,47 |
|
6 |
4,08 |
0,59 |
0,41 |
11 |
9 |
1559 |
0,85 |
83,6 |
71 |
319,072 |
|
7 |
2,67 |
0,31 |
0,69 |
15 |
10 |
5674 |
3,34 |
117 |
392 |
719,35 |
|
8 |
1,36 |
0,77 |
0,23 |
11 |
8 |
3919 |
0,41 |
274 |
113 |
304,037 |
|
9 |
3,45 |
0,86 |
0,14 |
16 |
8 |
2523 |
0,33 |
136 |
44,2 |
399,841 |
|
10 |
1,59 |
0,56 |
0,44 |
19 |
10 |
3948 |
1,49 |
116 |
174 |
220,687 |
|
В приведенной таблице выберете свой
вариант. Проведите вычисления и
полученные результаты сравните с
ответами. |
Подставив эти значения в уравнение
производственной функции, получим:
P=k Lβ1 Cβ2=
1.01L0.75C0.25
Предположим, что цена труда (рабочей
силы) равна PL=12 долл.
за единицу (колонка 4), а цена капитала
PC =2 долл. за единицу
(колонка 5).
Предприятие смогло привлечь (занять)
денежную сумму в размере VC=1000
долл. (колонка 6).
Необходимо определить:
- Каково оптимальное соотношение между
вводимым трудом и вводимым капиталом?
-
Сколько единиц труда и капитала следует
приобрести данному производителю?
Какой будет максимальный выпуск
продукции?
Решения
 Что такое частные производные?
Что такое частные производные?
Помните вы изучали функцию спроса
QD= f (P), QD=
f (P, t, Tp, I,РR, E, N, А, О)),
при этом говорилось, что спрос зависит
от многих факторов. Решение такого
уравнения возможно при условии, если
мы фиксируем все переменные t, Tp,
I,РR, E, N, А, О=const и изучаем
только одну переменную QD=
f (P, const). Таким образом,
рассматривается частный случай
общего уравнения, или как говорят
математики: "Сначала возьмем частную
производную по Р". Производственная
функция также зависит от многих факторов
P'=1.01L0.75C0.25,
в нашем случае от L и С. Поэтому
…
а. Сначала возьмем частные производные,
чтобы определить численные значения
предельных продуктов труда и капитала,
используя которые можно будет применить
правило найма рабочей силы при наименьших
издержках.
Для чего продифференцируем
производственную функцию по L:
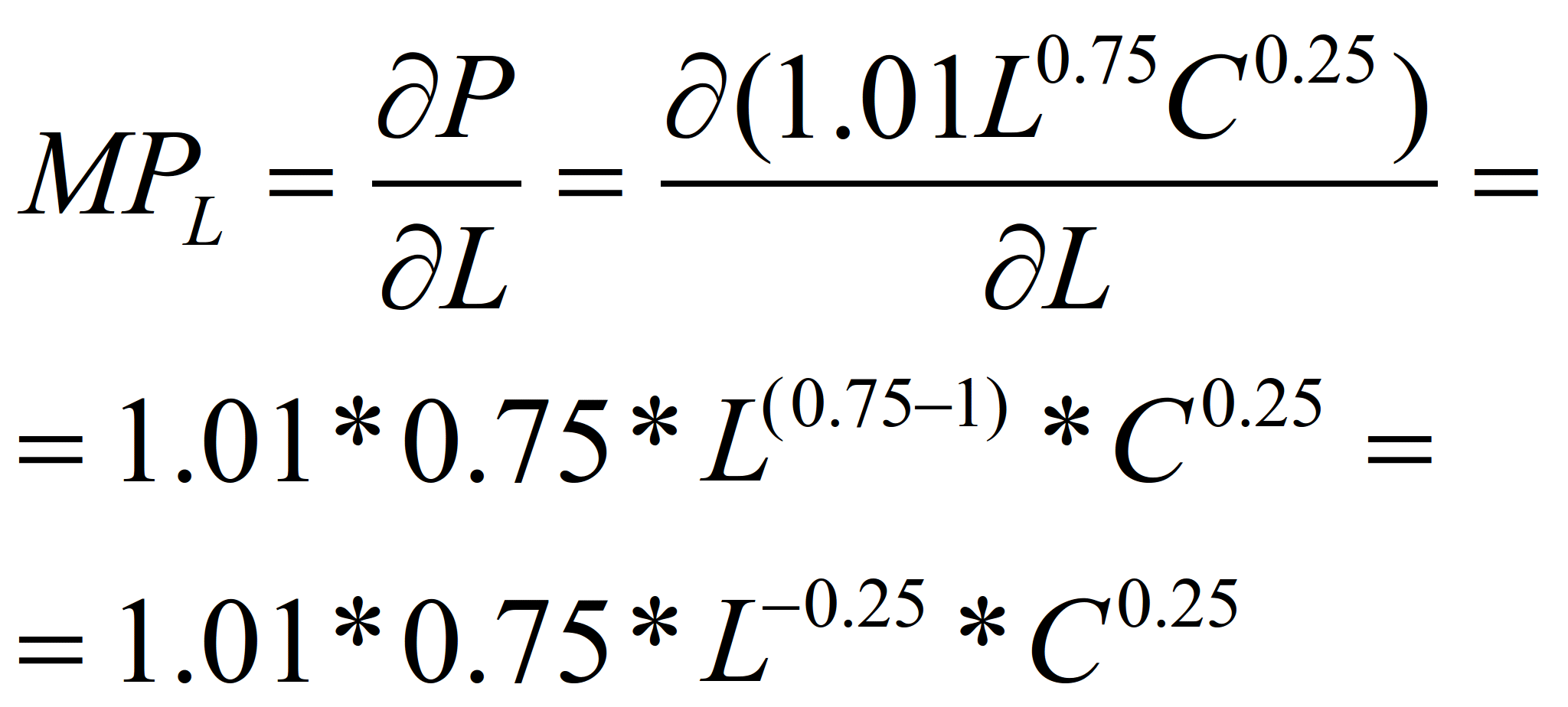 (21)
(21)
и по С.
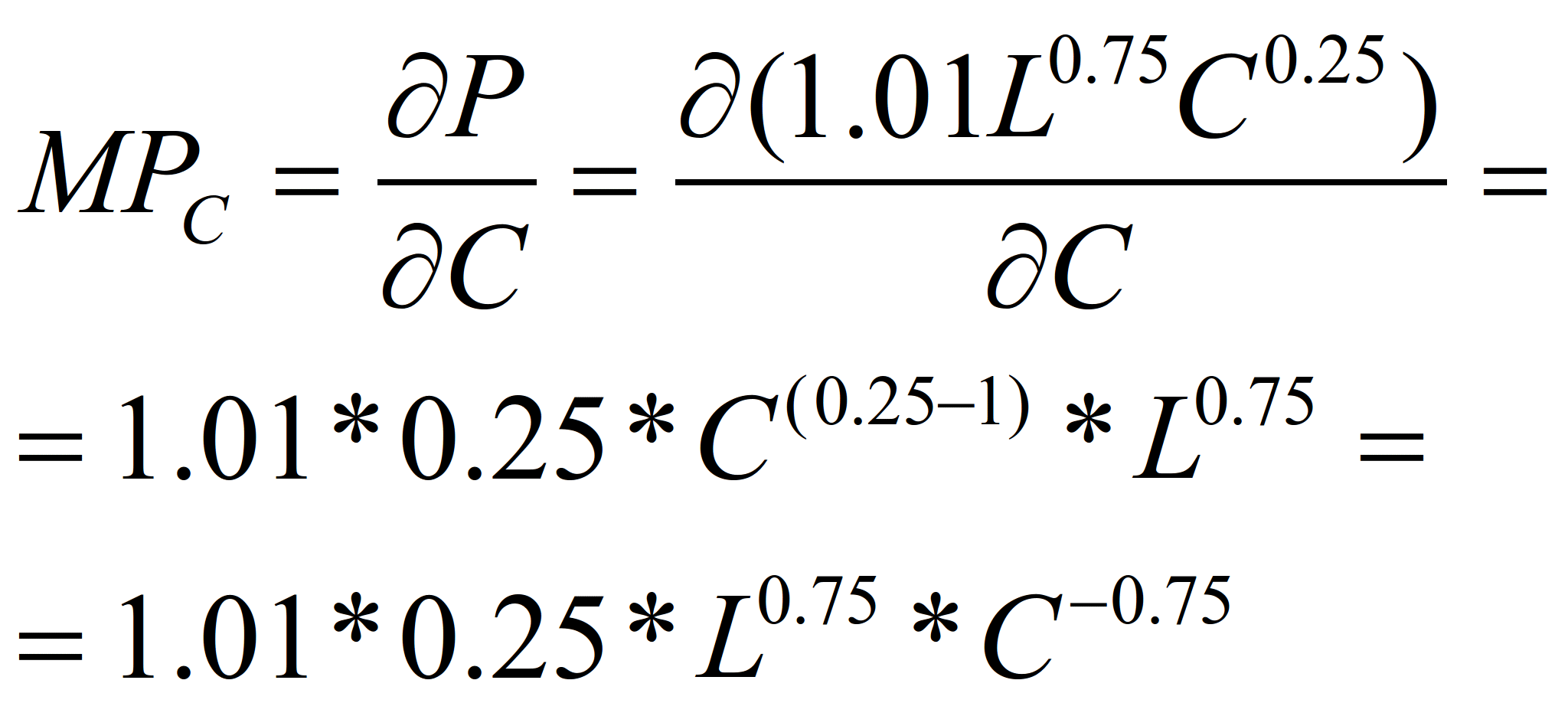 (22)
(22)
Напомним если исходная функция хm
(m – постоянная), то ее производная
будет равна m* хm-1, т.е.
d(L0.75)/dL=0.75*L0,75-1=0,75*L-0,25.
Кроме этого, когда мы дифференцируем
по одной из переменных, то другие
переменные постоянны.
Выразим отношение численных значений
предельных продуктов через значения
труда и капитала:
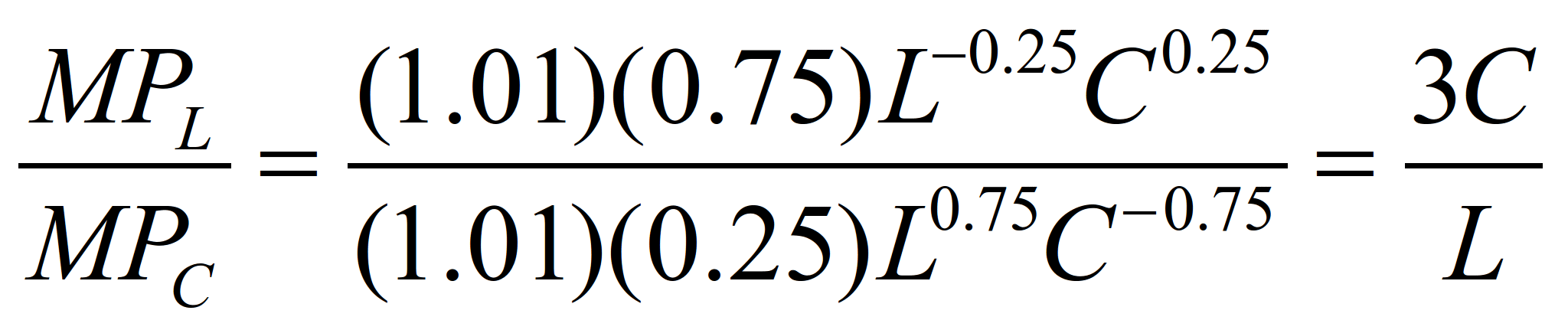 (23)
(23)
Правило найма рабочей силы при
наименьших издержках
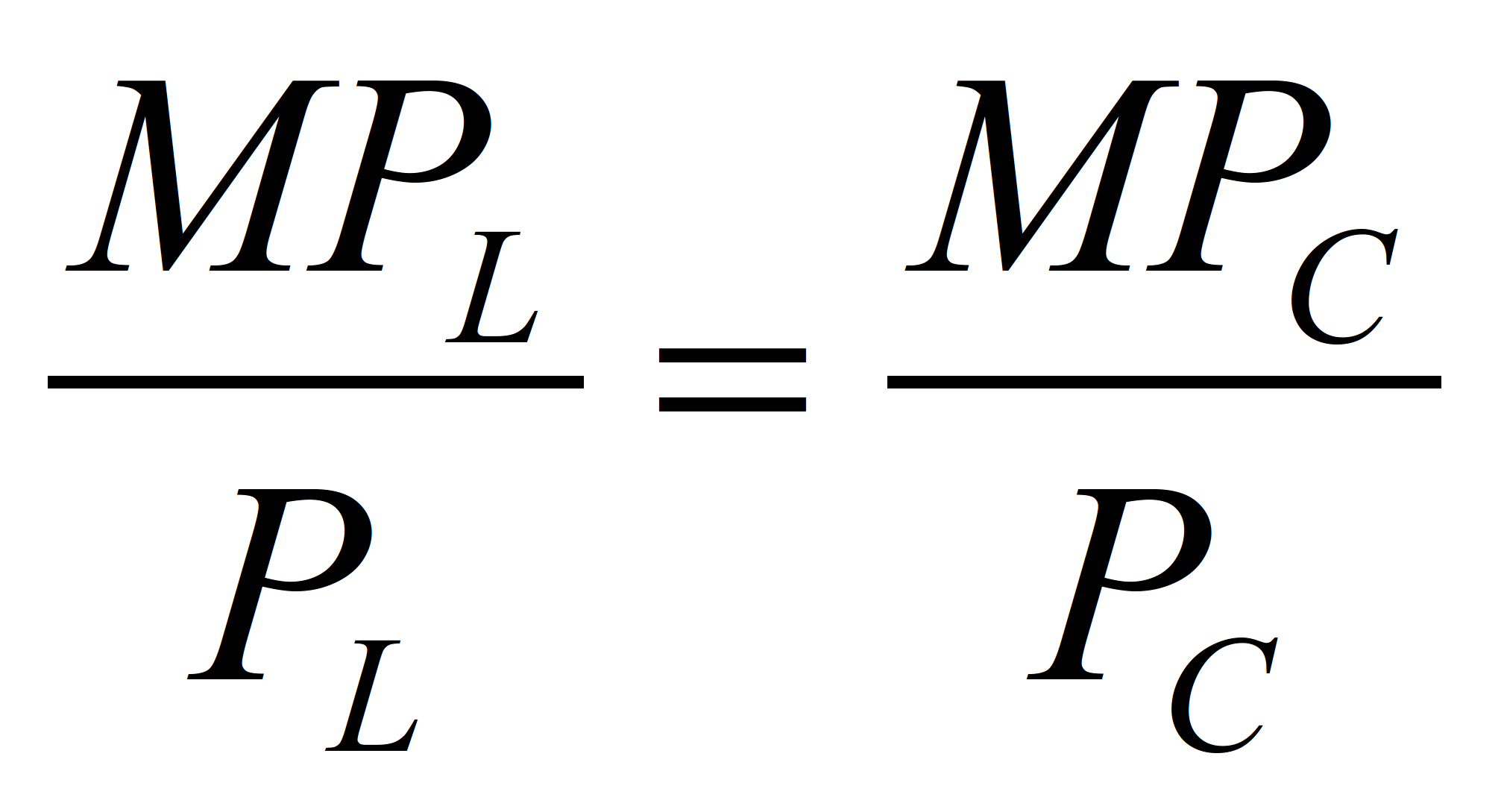
может быть также представлено в виде:
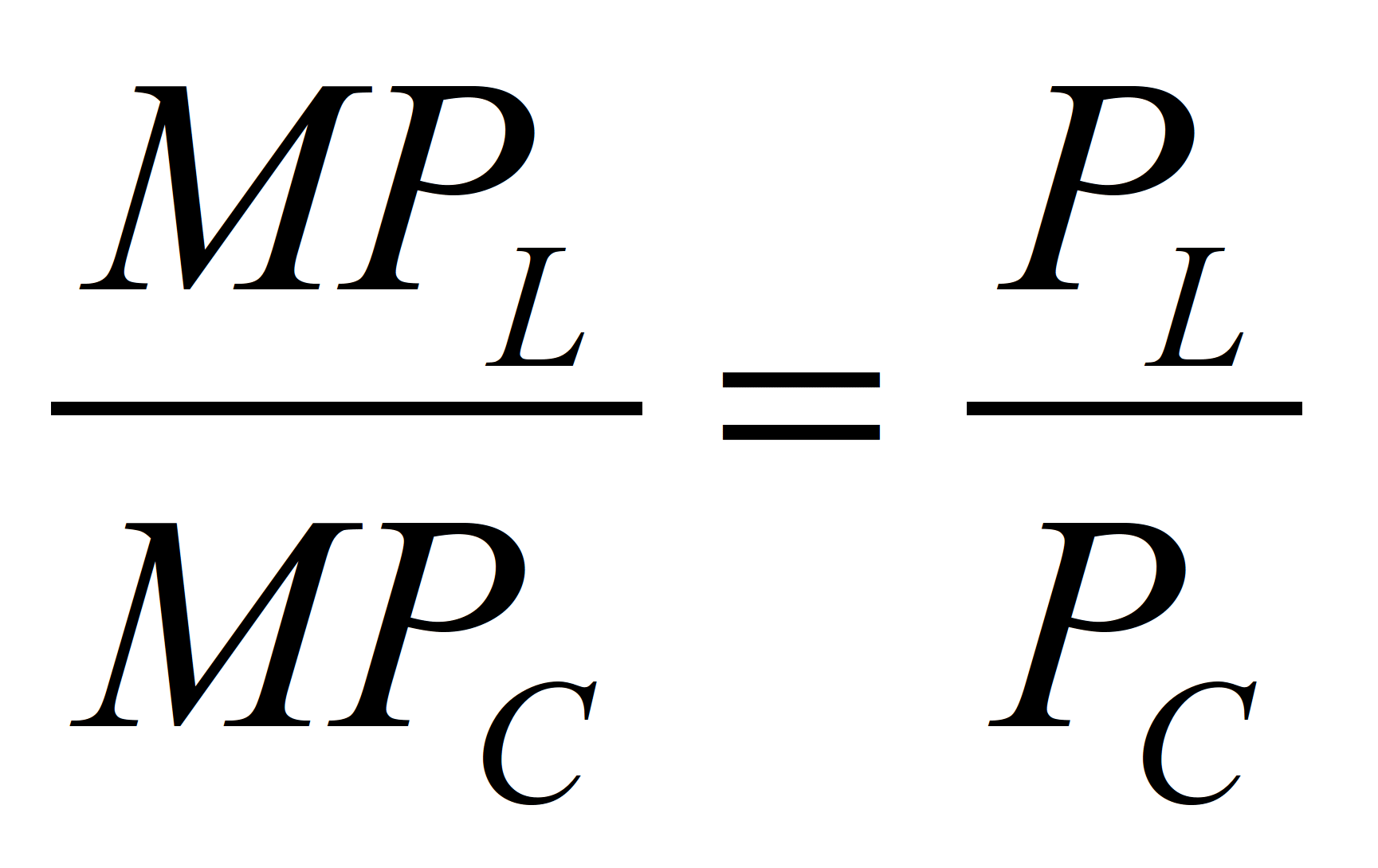 (24)
(24)
Следовательно,
3C/L=12/2
C/L=2 (см. колонка 7)
Выполнив перекрестное умножение, мы
получим:
6С=12L
C=2L
Из последнего соотношения видно, что
независимо от количества единиц
изделий, которые должны быть произведены,
производитель всегда должен использовать
две единицы капитала на каждую единицу
труда.
Изложенная ранее процедура определения
оптимального соотношения вводимых
факторов производства (с использованием
частных производных для определения
предельных продуктов) может быть с
успехом использована для исследования
производственных функций любого вида,
включая степенную функцию.
Степенная функция обладает особыми
свойствами, которые дают возможность
воспользоваться значительно более
легкой и удобной для вычислений упрощенной
формулой. Эта упрощенная формула в
общем виде, может быть представлена
как:
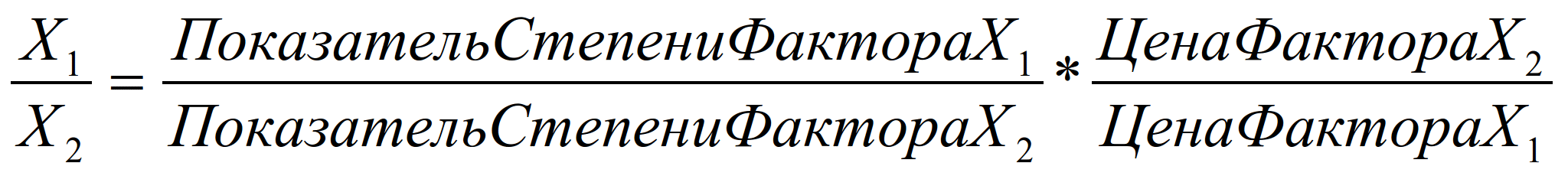 (25)
(25)
где X1 и X2
- количества двух различных вводимых
факторов производства.
Применяя общее уравнение к нашей
конкретной задаче и полагая X1
= С, a X2 = L, мы
получаем тот же самый ответ при значительно
меньших затратах времени на вычисления.
Если некоторая степенная функция
содержит больше двух переменных вводимых
факторов производства, то в таком случае
упрощенная формула может быть
использована для вычисления оптимального
соотношения любой пары одновременно
изменяющихся вводимых факторов, которые
входят в эту степенную функцию.
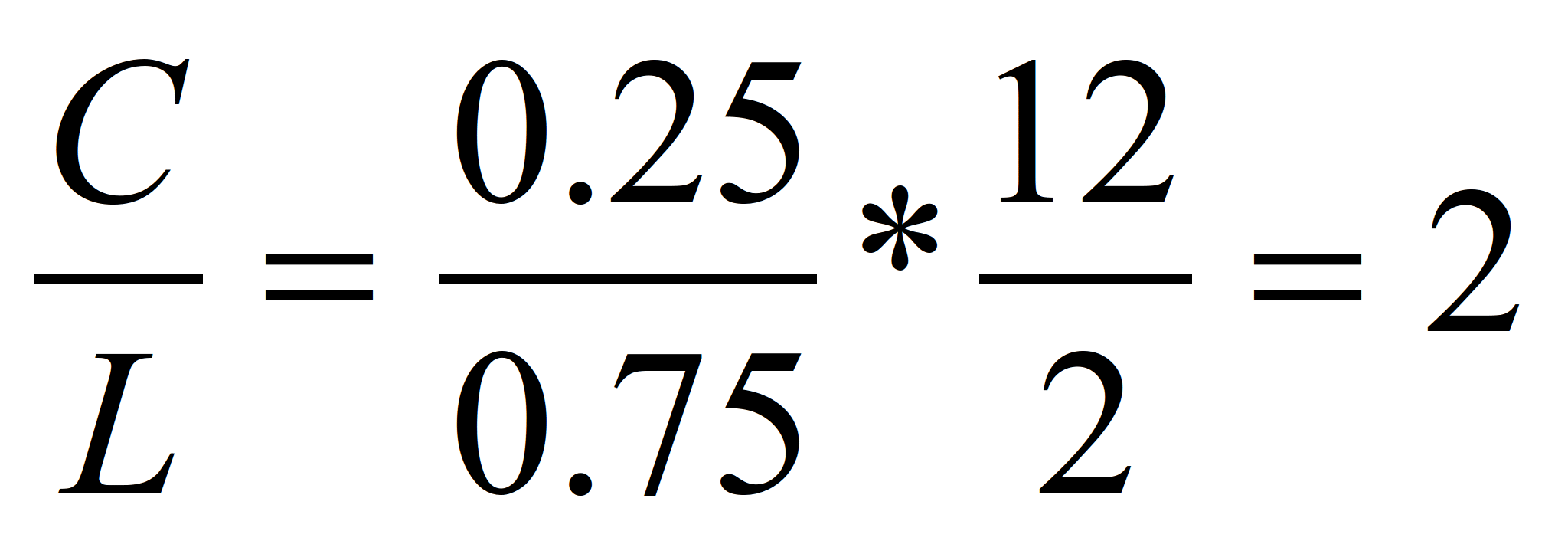 (см. колонка 7)
(см. колонка 7)
откуда
C=2L
L=0.5C
б. После того, как найдено оптимальное
соотношение вводимых факторов
производства, максимальное количество
единиц изделий, которое может быть
произведено, определяется той суммой
денег, которой располагает производитель
для найма рабочей силы или для приобретения
прочих вводимых факторов. Поскольку в
настоящей задаче стоимость труда
составляет 12 долл. за единицу, а
стоимость капитала - 2 долл. за
единицу, то в таком случае общие издержки
составят:
TC=L*PL+C*PC=12L+2C
Предположим, что мы располагаем
возможностью затратить на приобретение
рабочей силы и капитала максимум 1000
долл. Тогда
12L + 2C = 1000.
Но поскольку С=2L постольку,
подставляя вместо величины С
выражение 2L мы получим:
12L+ 2(2L)=16L=1000;
L=1000/16=62,5; (см. колонка 8)
C=2L=125 (см. колонка 9)
Конечно, мы могли бы получить тот же
самый ответ, подставляя выражение 0,5С
вместо величины L, поскольку L=0,5С:
12L+ 2C= 1000;
12(0,5C) + 2C= 1000;
8C= 1000;
C = 1000/8 = 125;
L = 0.5C = 62,5
Если мы подставим два последних
результата в исходное уравнение, то
получим:
P=1,01L0.75C0.25=(1,01)(62,5)0,75(125)0,25=75,069
(см. колонка 10)
Данное выражение можно вычислить
также с помощью логарифмирования левой
и правой частей уравнения:
LgP=lg1.01+0.75LgL+0.25Lg(C)=
=lg1.01+0.75Lg(62.5)+0.25Lg(125)=1.8754
Откуда
P=101.8754=75.069 (см. колонка
10)
Таким образом, если предприятие
ограничено суммой в 1000 долл., то в
таком случае максимальный уровень
выпуска продукции составит приблизительно
75 единиц.
 добрений
на производство картофеля. Наряду с
удобрениями, урожай картофеля зависит
от целого ряда других факторов
производства, таких, как почва
(земля), вода (дождевая или вода для
орошения), солнечный свет, температура
и труд. Но в данном исследовании в
качестве переменного фактора производства
используются только удобрения.
добрений
на производство картофеля. Наряду с
удобрениями, урожай картофеля зависит
от целого ряда других факторов
производства, таких, как почва
(земля), вода (дождевая или вода для
орошения), солнечный свет, температура
и труд. Но в данном исследовании в
качестве переменного фактора производства
используются только удобрения.
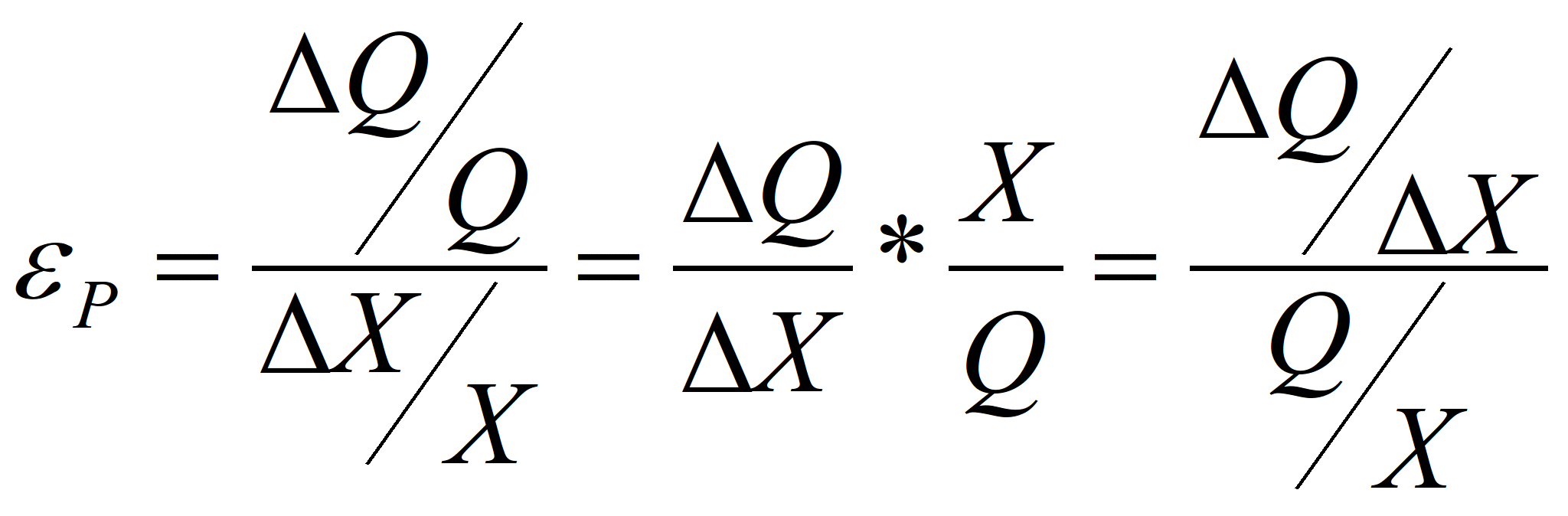 (4)
(4)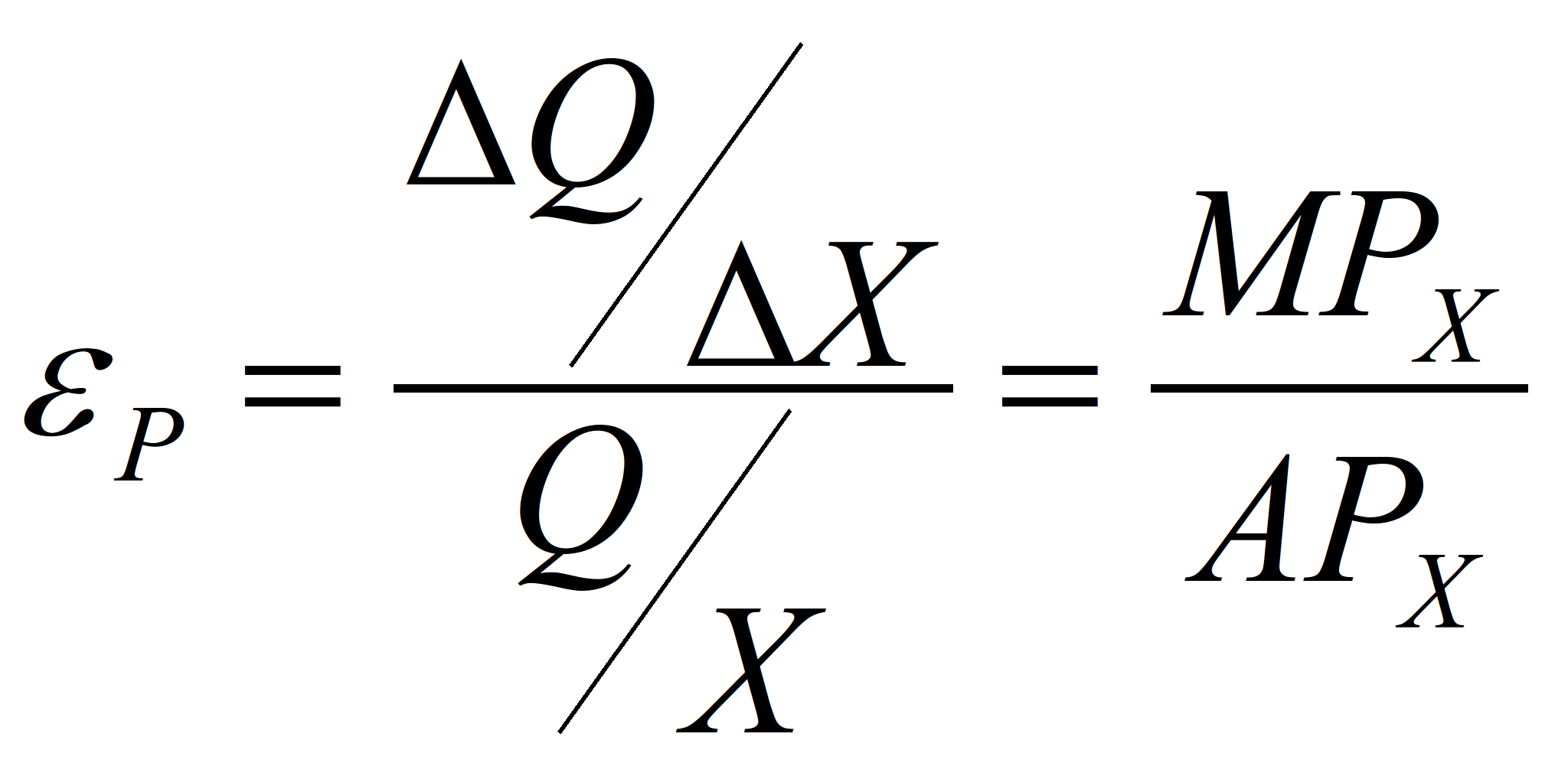 (5)
(5)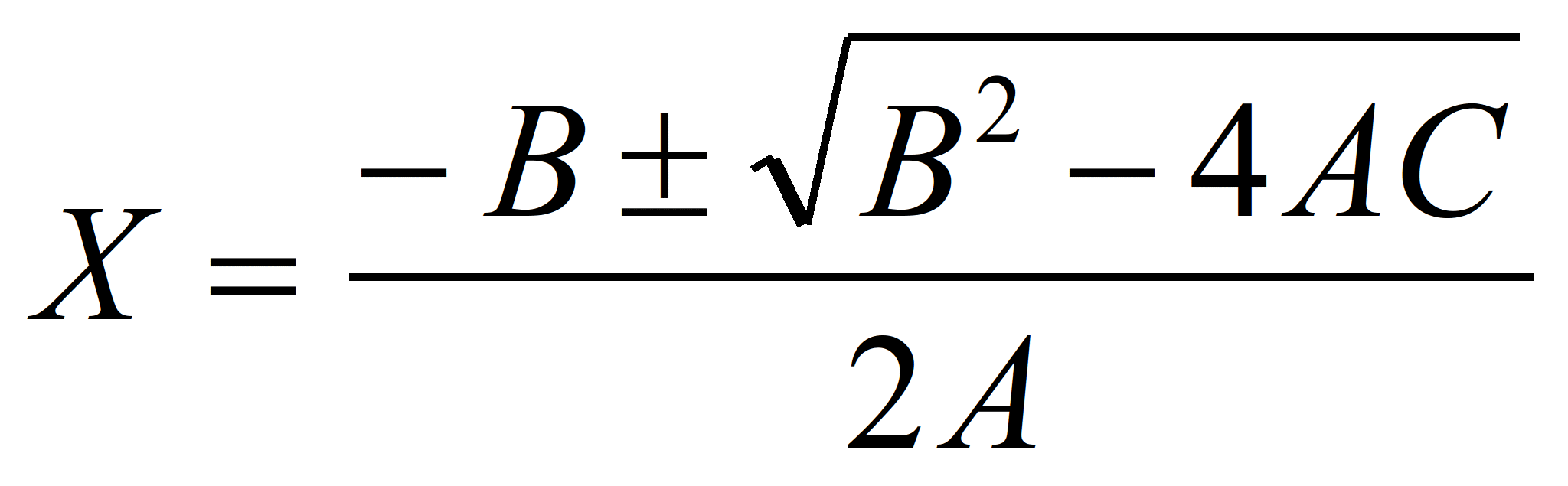
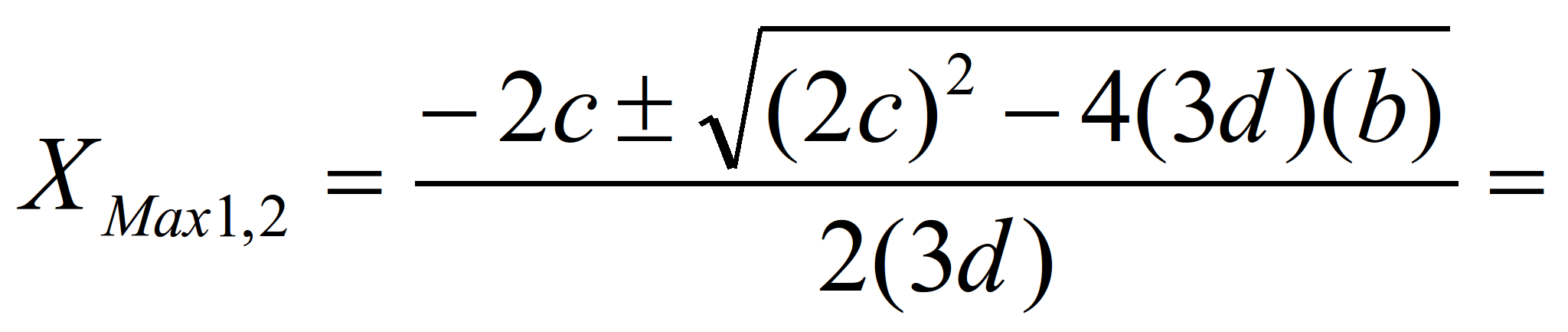 -0,503
или 8,478 (см. колонка 2, 3)
-0,503
или 8,478 (см. колонка 2, 3)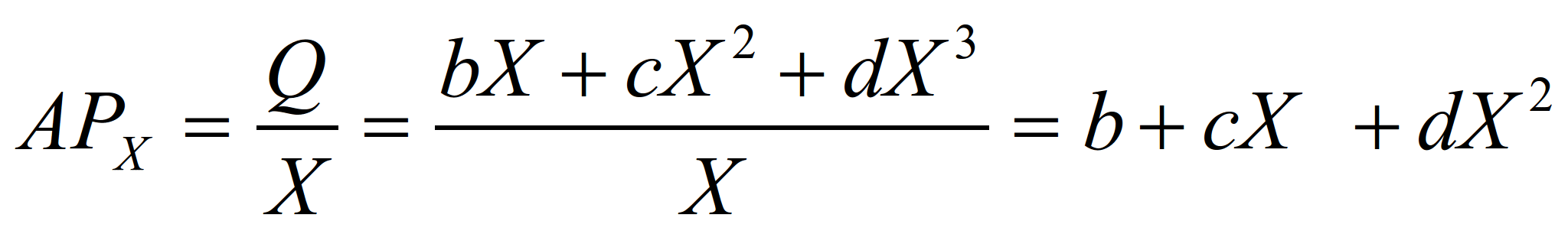 (6)
(6)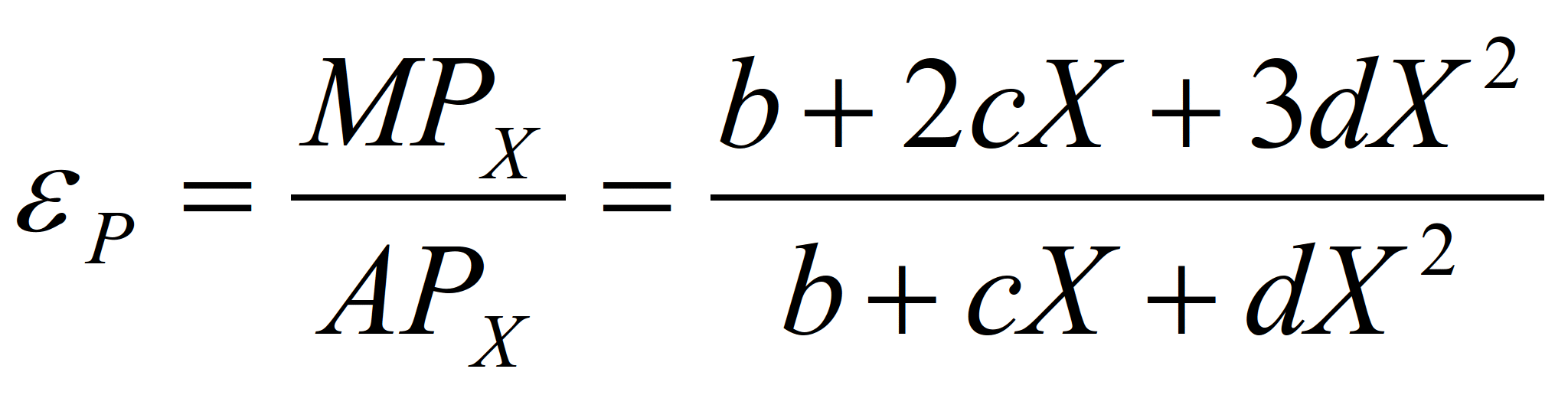 (8)
(8)

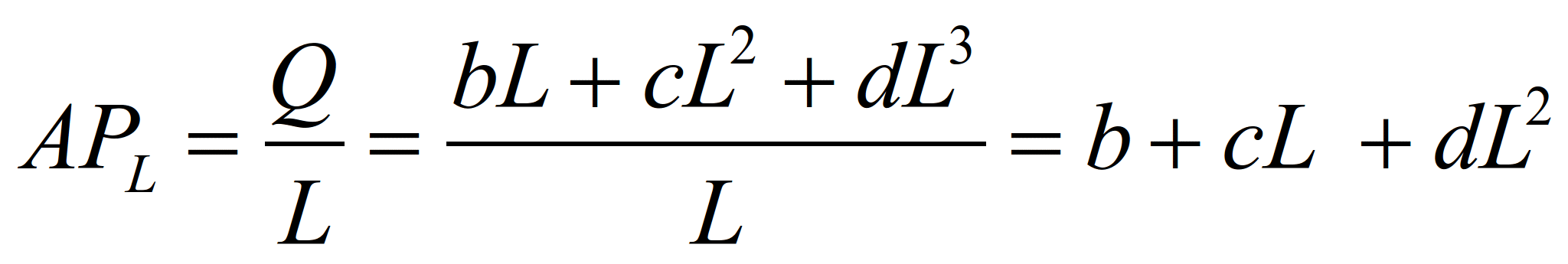
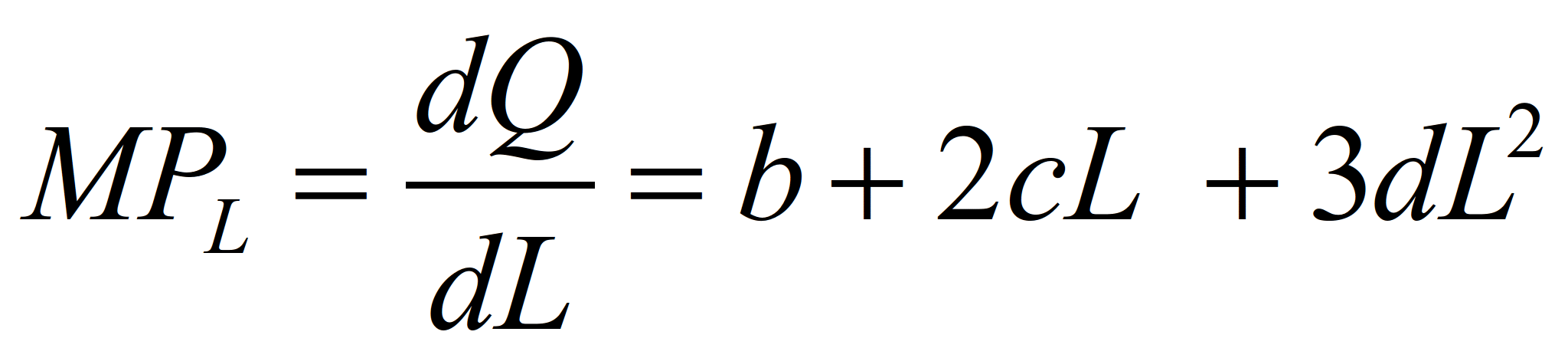
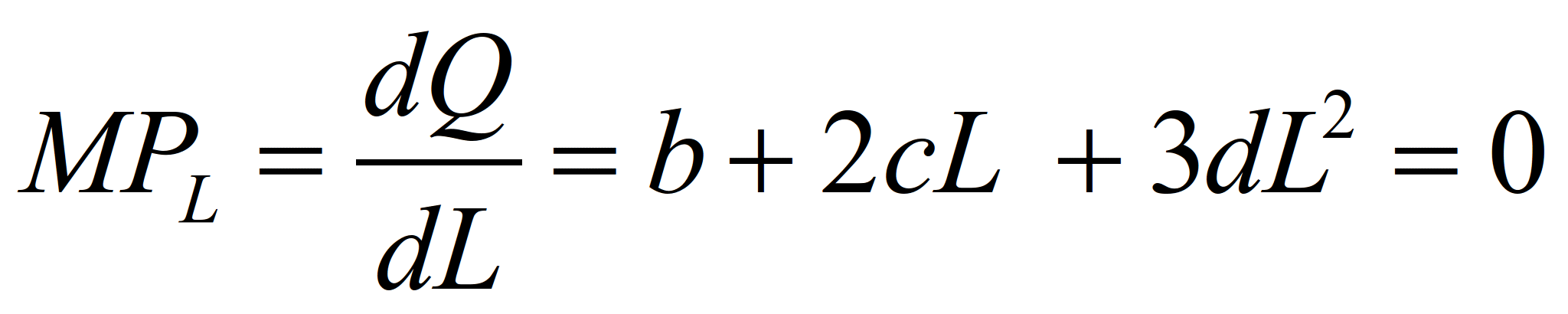
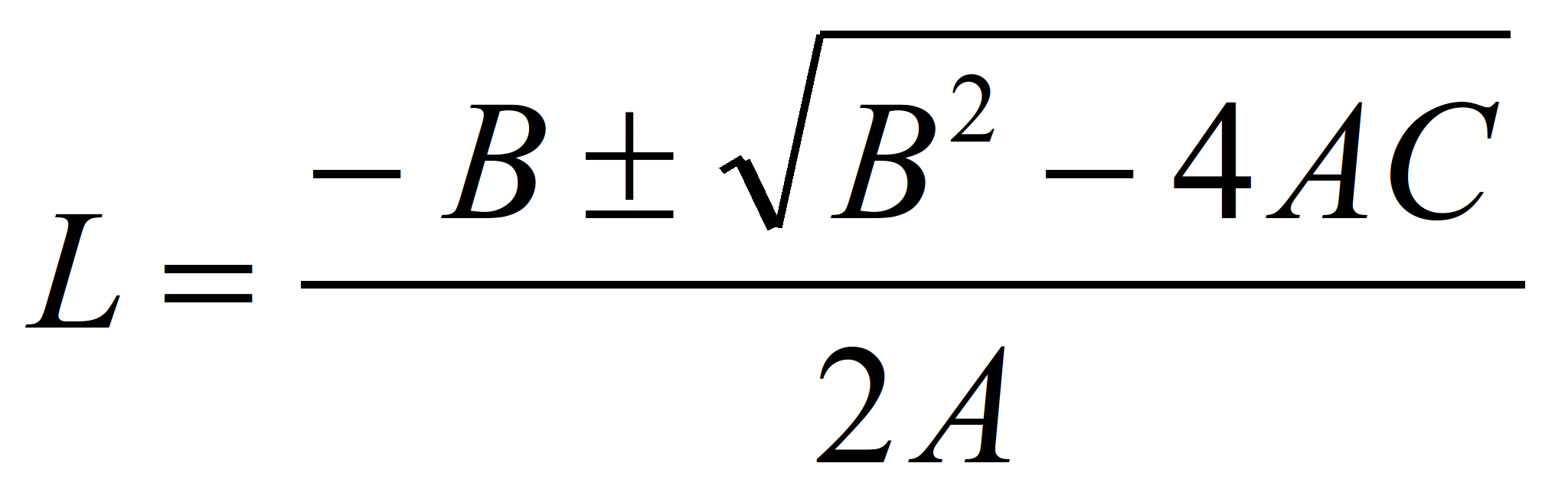 (11)
(11)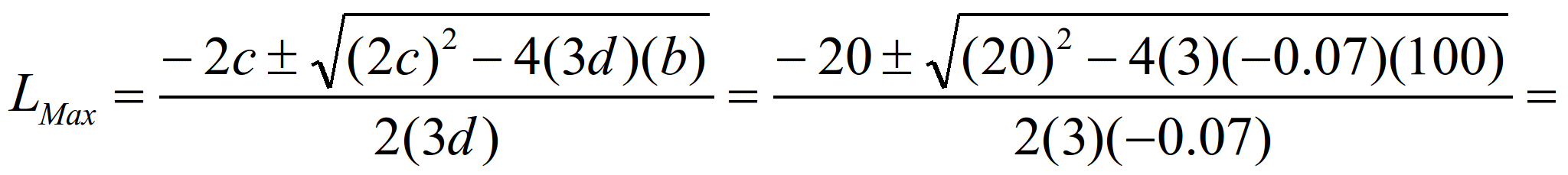 -4,7619
или 100 (см. колонка 6 и рис. 2)
-4,7619
или 100 (см. колонка 6 и рис. 2)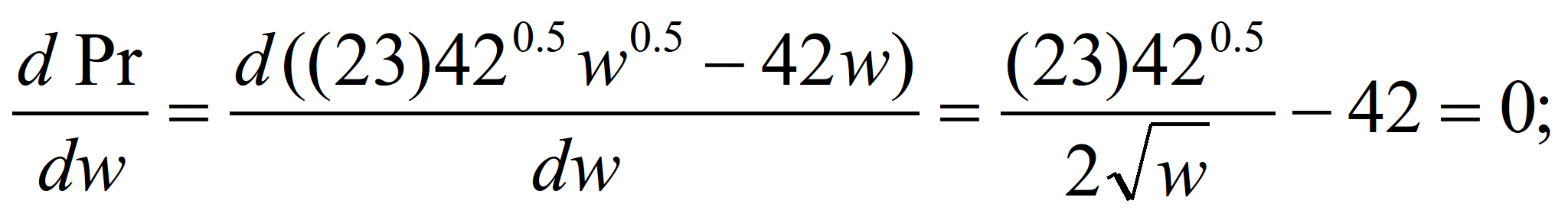
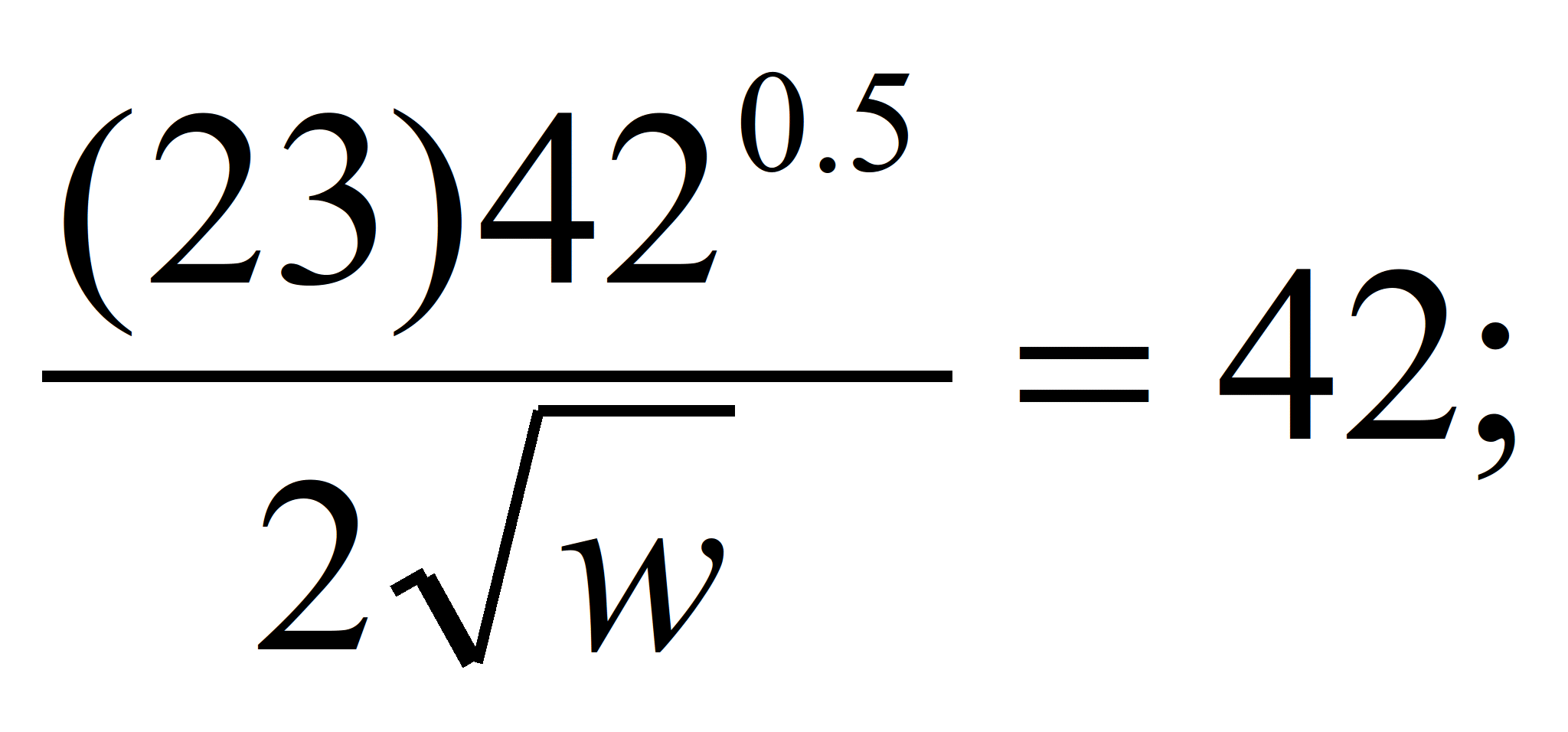
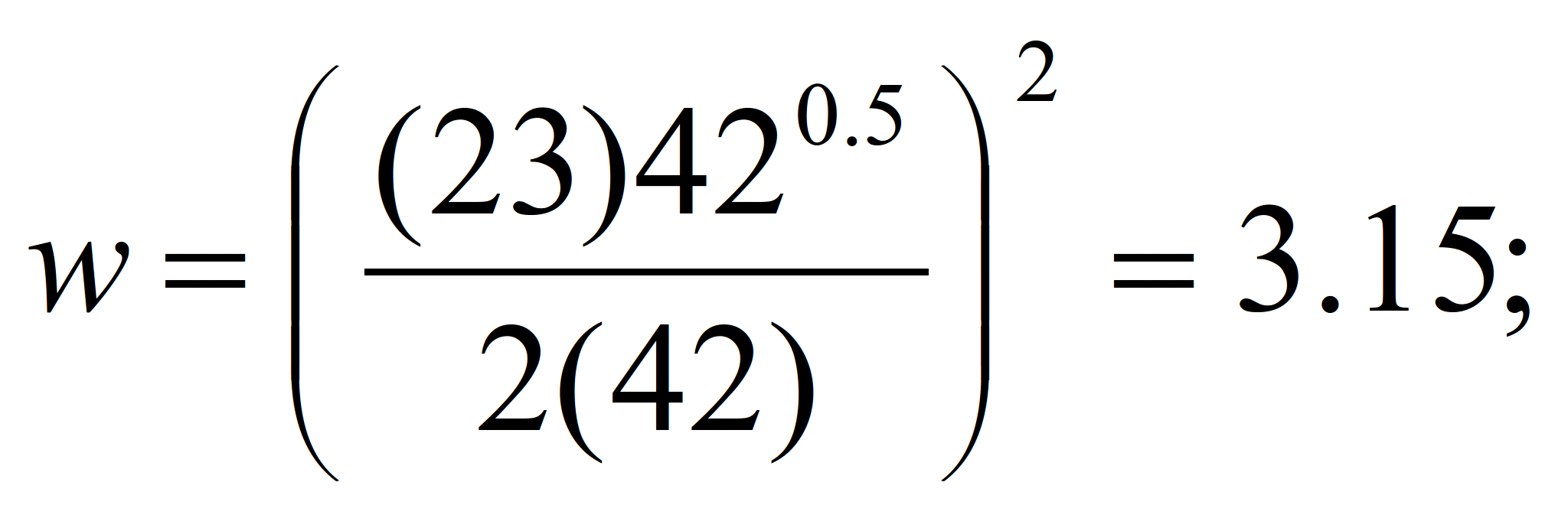
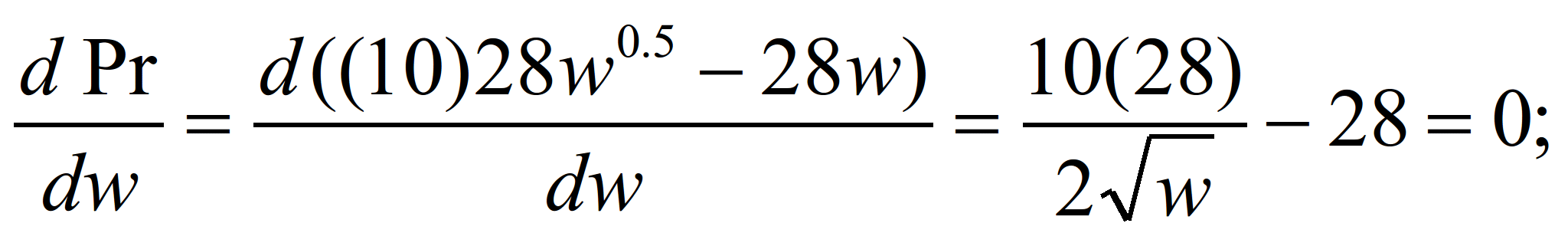
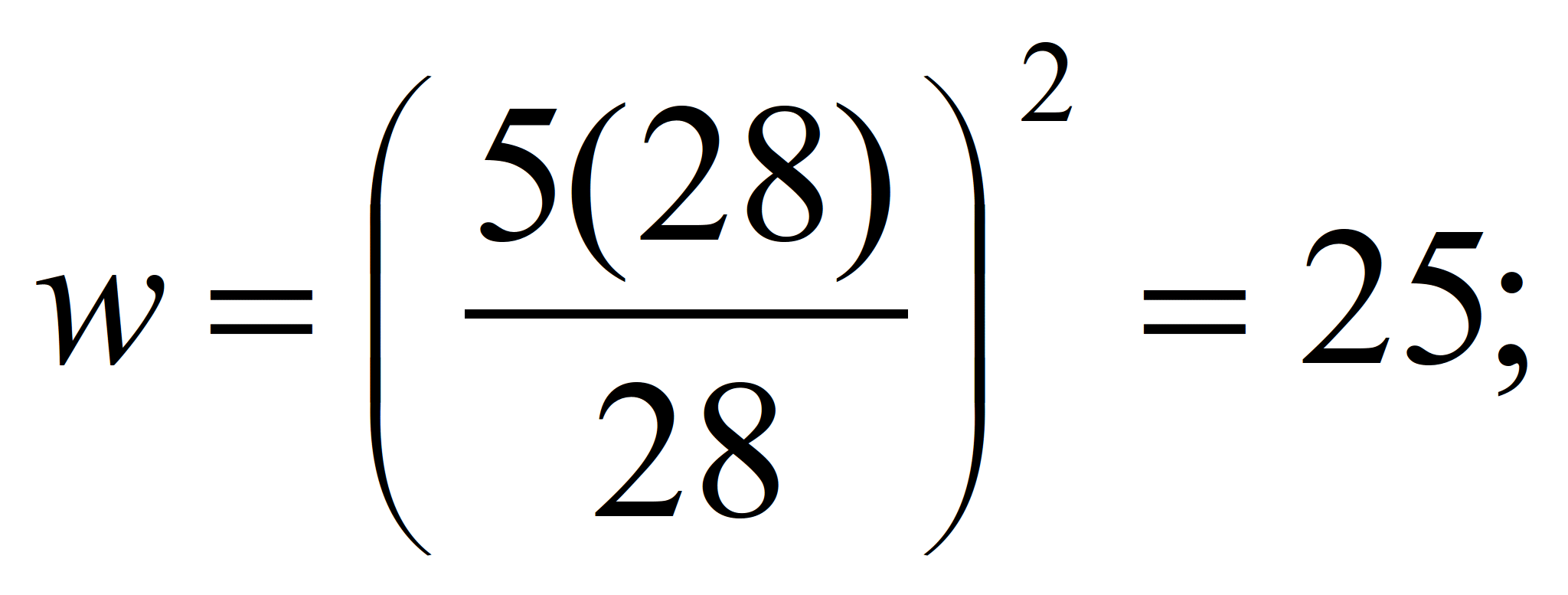
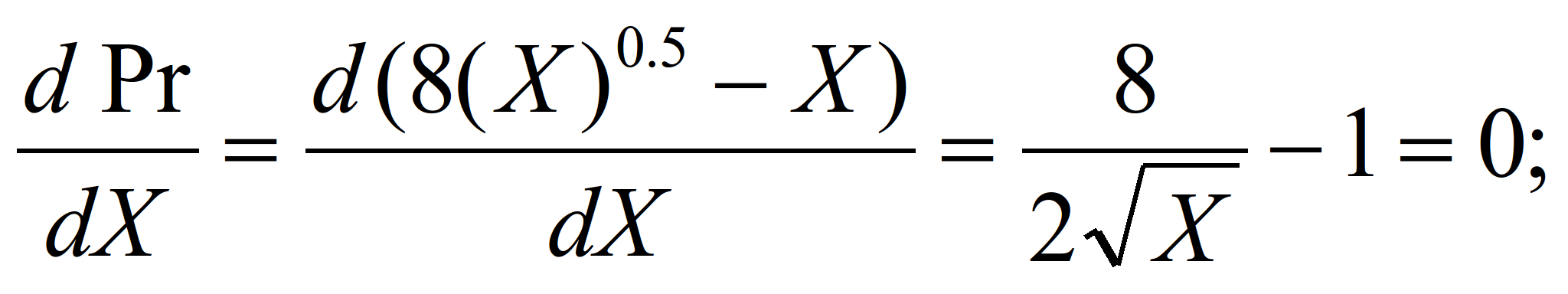
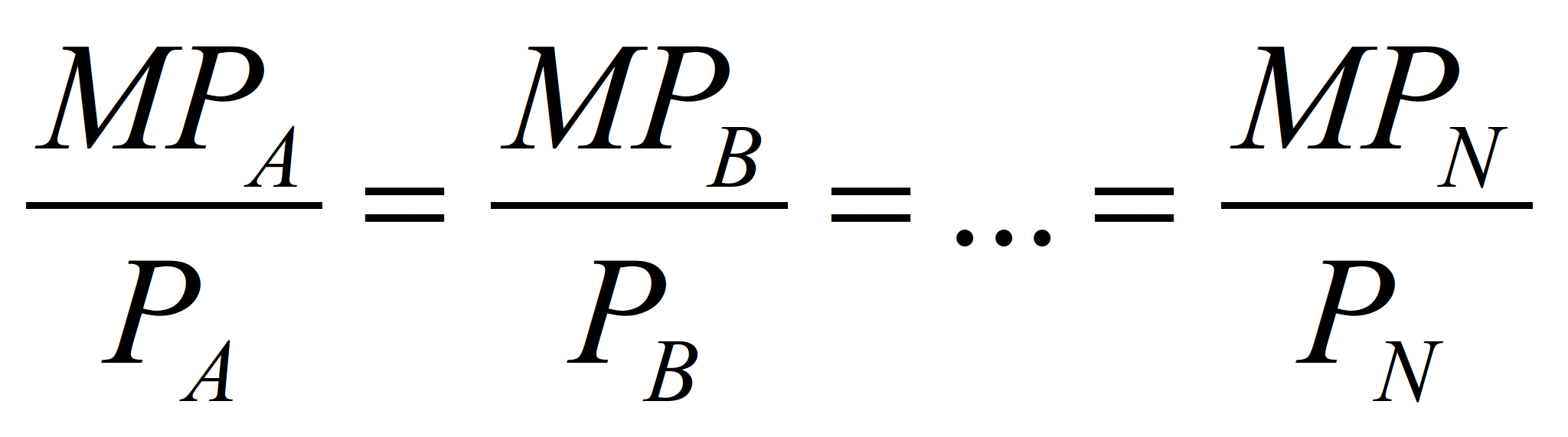 (18)
(18)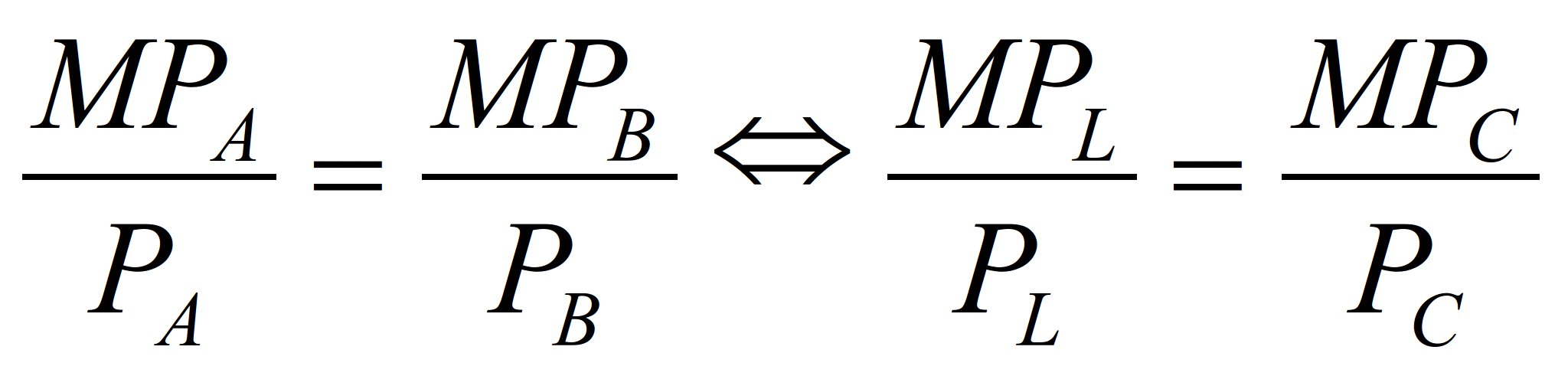 (19)
(19)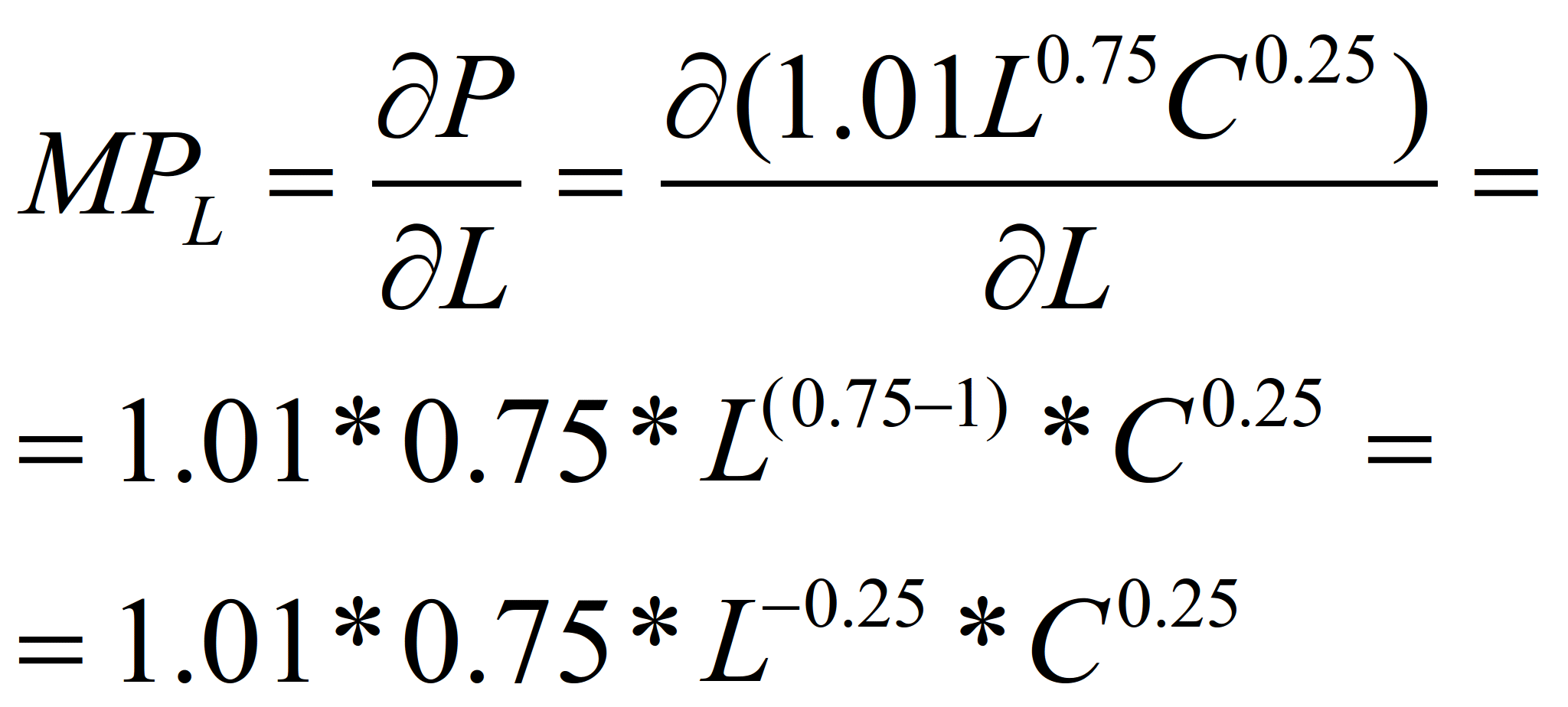 (21)
(21)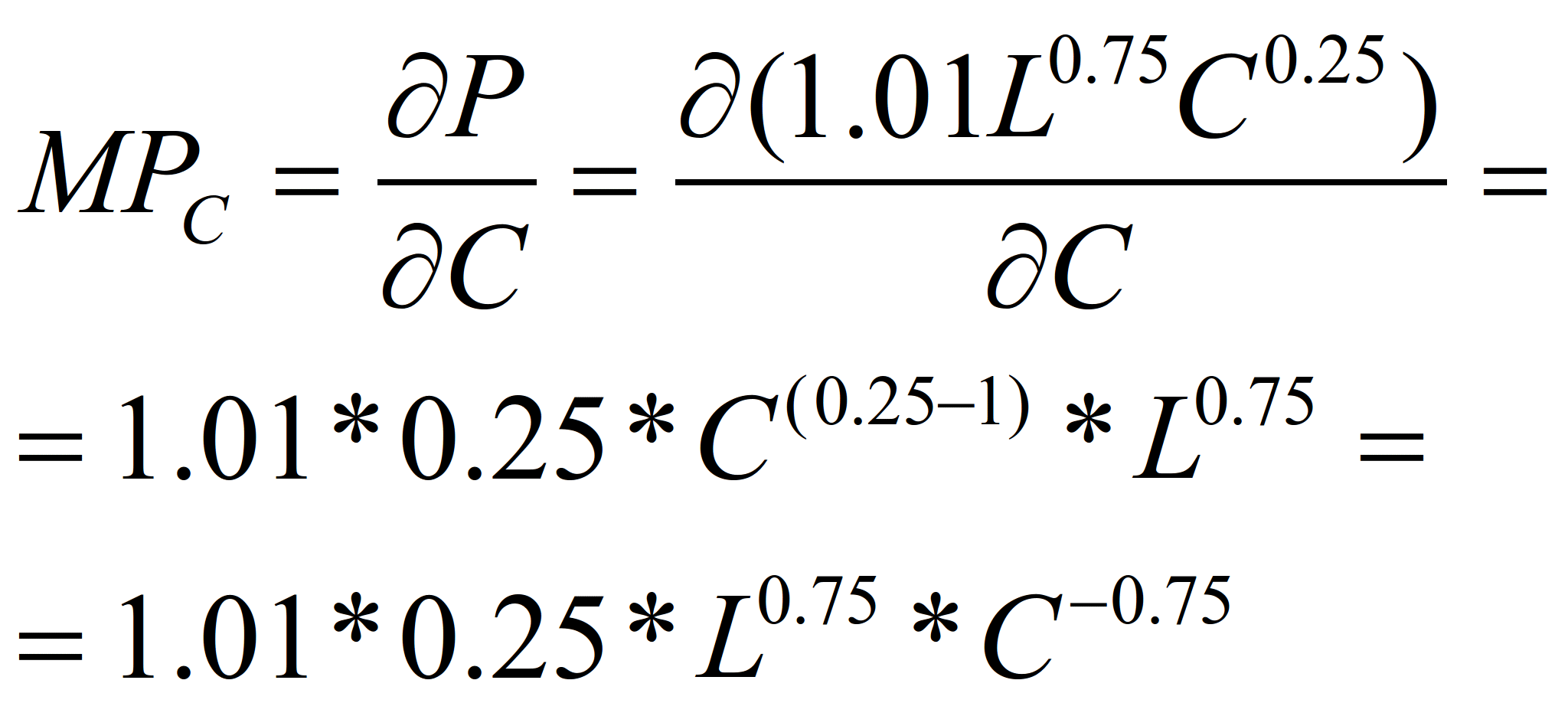 (22)
(22)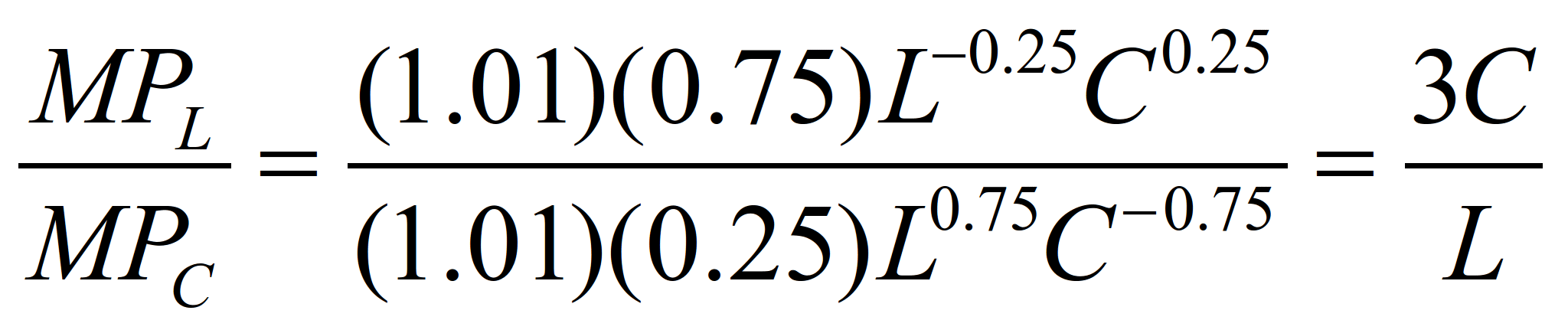 (23)
(23)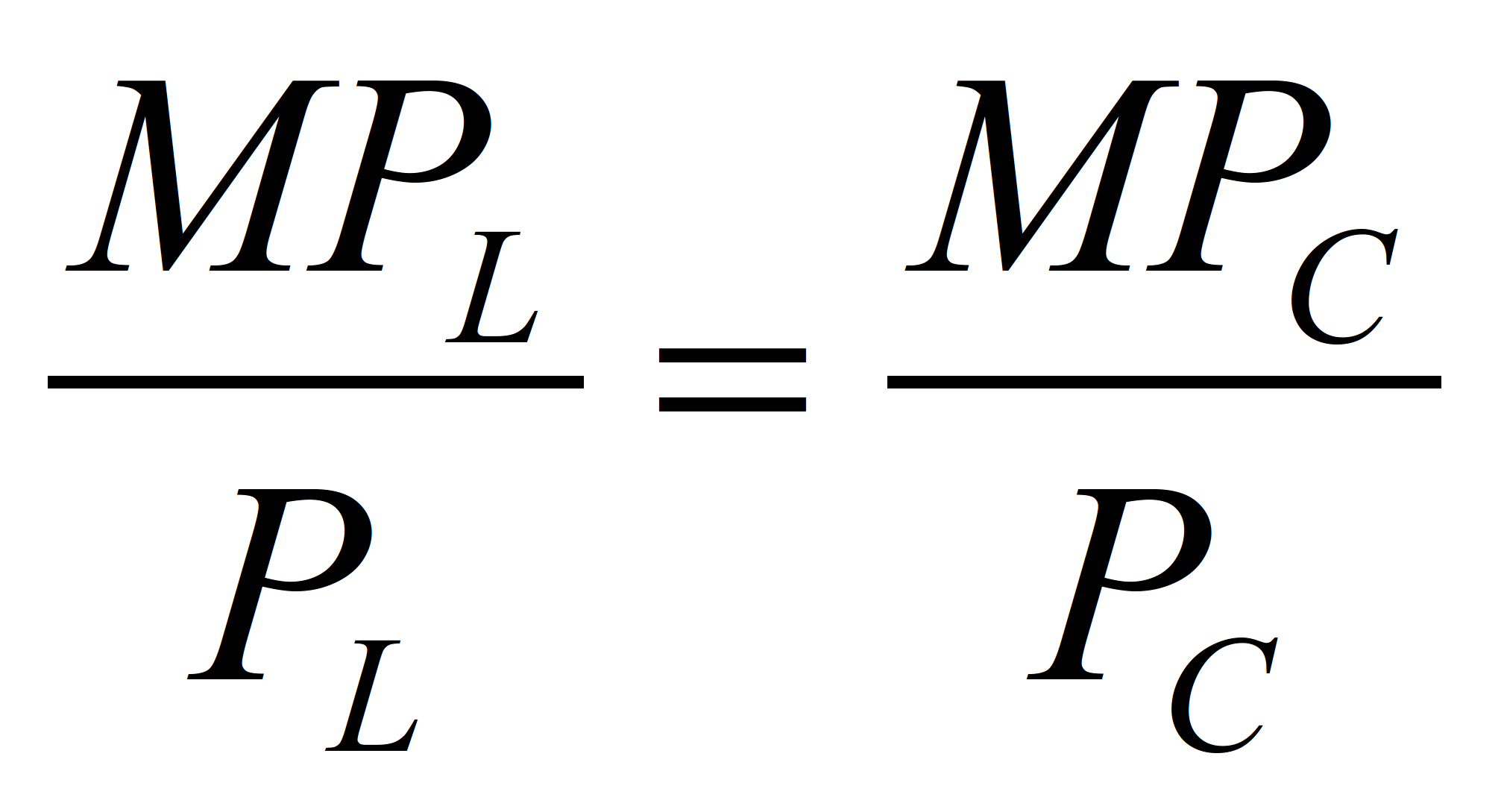
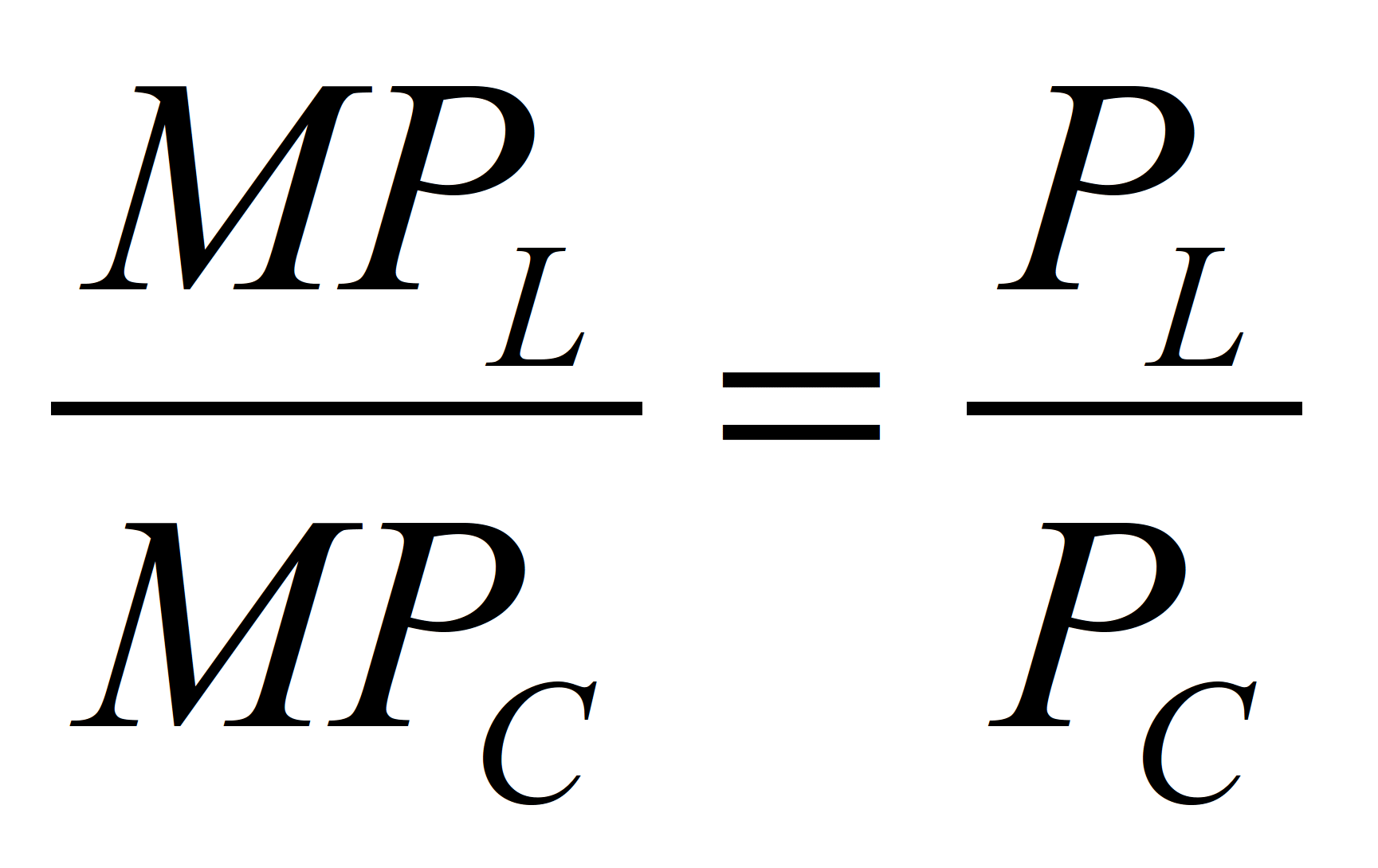 (24)
(24)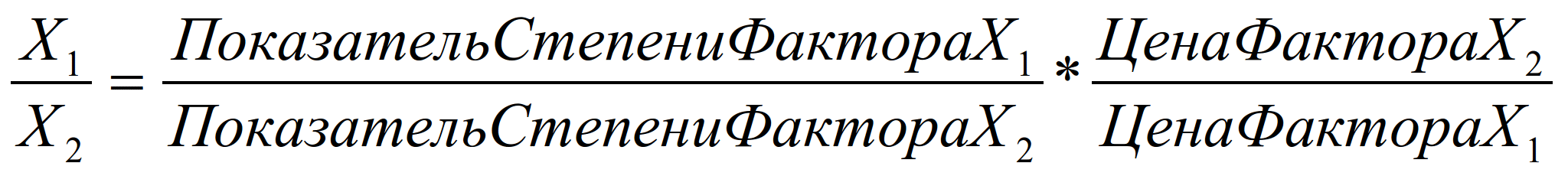 (25)
(25)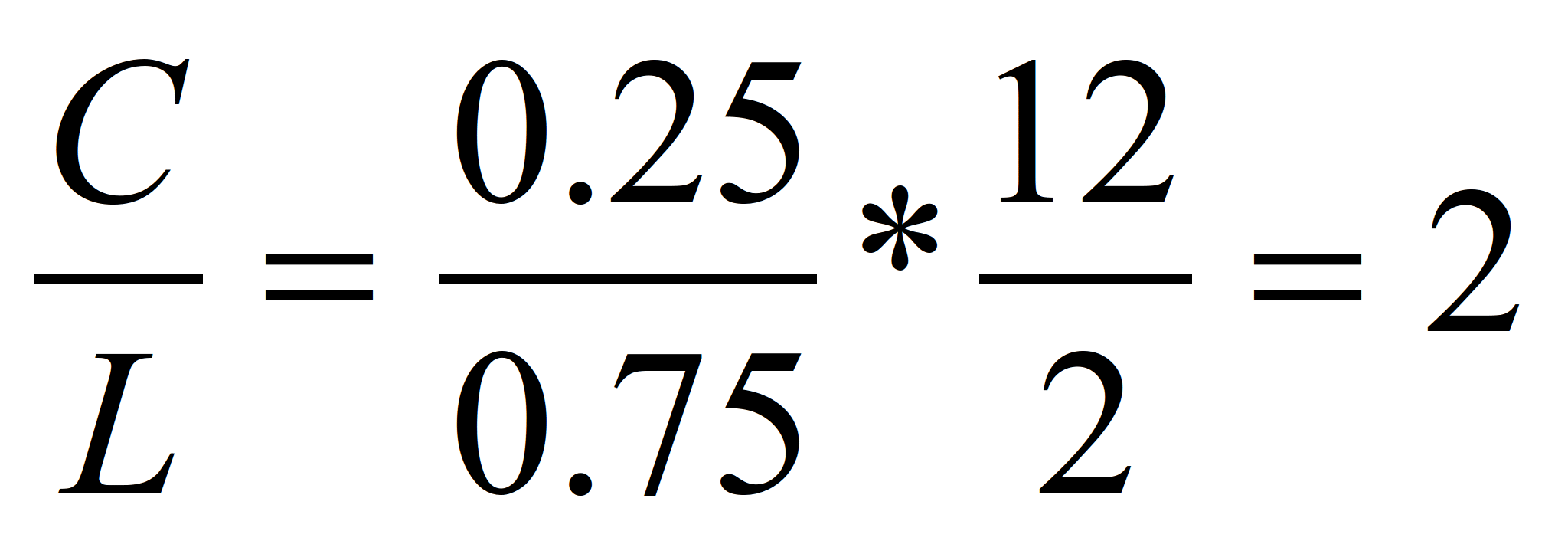 (см. колонка 7)
(см. колонка 7)