2.1.

СПРОС И ПРЕДЛОЖЕНИЕ

В основе деятельности семейного хозяйства, предприятия, правительства, рынков товаров и услуг, финансовых, сырьевых (ресурсных) лежит закон спроса и предложения.

Предприятие должно понимать динамику сил, влияющих на спрос и предложение, и уметь управлять этими силами с целью повышения прибыльности. Предприятие должно знать, будут ли покупать его продукцию на рынке.

При разработке разделов бизнес-плана предприятию необходимо оценить ожидаемый спрос на продукцию и уровень затрат на труд, капитал и другие ресурсы.

Цели

• Понять поведение потребителя и построить модель его поведения.
• Описать закон спроса и факторы на него влияющие.
• Описать закон предложения и факторы на него влияющие.
• Объяснить взаимосвязь между спросом и предложением.
• Понять смысл коэффициента эластичности спроса и предложения.

Ключевые термины и концепции

• Закон убывающей полезности.
• Функция полезности.
• Равновесие потребителя.
• Предельная полезность и кривые спроса.
• Эффект дохода и замещения.
• Спрос и факторы, влияющие на него.
• Предложение и факторы, влияющие на него.
• Эластичность, ее виды.

Любой человек (покупатель, продавец) воспринимает окружающий мир через свое индивидуальное ощущение полезности тех товаров и услуг, которые он бы желал иметь. Но это желание не безгранично, оно убывает по мере получения желаемого. Это и отражает закон убывающей полезности. Но кроме желания нужно иметь возможность оплатить данный товар, т.е. необходимы деньги. При наличии желания и денег человек может теперь купить товар, формируя индивидуальный спрос. Очень часто вкусы и желания людей совпадают, что определяет совокупный спрос (спрос многих людей). Рынок является тем местом, где встречаются и продавцы и покупатели.

Рынок предполагает наличие продавцов, покупателей (потребителей), конкуренции между ними, товаров, денег. Спрос на рынке формируют потребители и их кошельки (наличие у них денег, а не только желание купить). Поэтому потребители (покупатели) являются главными на рынке. Продавцы формируют предложение. Равновесие на рынке возникает только тогда, когда желание продавцов продать свою продукцию по их ценам совпадает с желанием и возможностью (наличие денег) покупателей купить эту продукцию.

Механизм рыночного равновесия можно упрощенно представить следующим образом:

• Чем больше желание и денег у покупателей купить предлагаемую продукцию, тем выше конкуренция и спрос среди потребителей, поэтому цены естественно начинают расти.
• Чем больше продавцов желают продать один вид товара, тем выше среди них конкуренция, которая приводит к снижению цен.

Когда желания и возможности покупателя и продавца совпадут, то на рынке будут сформированы равновесные цены

Практическое значение

Для фирмы, ставящей цель получения прибылей, изучение спроса является важной частью планирования бизнеса.

Почему мы покупаем товары или услуги? Очевидно, наше решение о покупке базируется на двух соображениях: полезности, которую можно извлечь из продукта, и нашей покупательной способности.

Экономисты определяют полезность как удовольствие, или удовлетворенность, связанную с обладанием, использованием или потреблением товаров или услуг (продуктов). Полезность имеет много источников и причин. Это происходит потому, что полезность является функцией индивидуального вкуса, предпочтения, восприятия, состояния мышления или образования личности. Более того, полезность - это не абсолютная величина. Она разная для каждого человека. Кроме того, даже для одного человека она меняется в зависимости от времени и места. Однако на момент принятия решения о покупке каждый потребитель оценивает полезность продукта и базирует свое решение покупать или не покупать на этом восприятии.

Функция полезности

Полезность будем измерять в условных единицах полезности. Проблема, однако, состоит в том, что никто не может определить эту единицу, поэтому фактически невозможно измерять полезность таким образом. Тем не менее, аналитически мы сделаем это для того, чтобы понять закон убывающей предельной полезности и далее вывести законы спроса и предложения.

Вы этот закон не только хорошо знаете, но и сталкиваетесь с ним постоянно. Например, жарким летом в полдень вы не прочь отведать мороженое, но если вы еще и голодны, то это желание становится настолько сильным, что вы готовы съесть его очень много. Это желание, как отмечалось ранее, зависит от времени и места. Например, зимой в 20 градусный мороз потребность в нем может вообще отсутствовать.

Итак, приступим к эксперименту…

После того как вы съели первую порцию, ваше желание явно уменьшилось, после второй – еще более, после третьей … , а после двадцатой!? Вы наверняка на мороженое в ближайший месяц и смотреть не сможете.

Давайте опишем этот закон экономически и математически. Он впервые был сформулирован подробно Альфредом Маршаллом и до сих пор приводится во многих работах экономистов, например К.К. Сио.

Предельная полезность для потребителя убывает по мере роста потребления. Предельная полезность определяется как изменение в общей полезности, вытекающее из изменения на одну единицу в потреблении, т.е.

(0)

где MU_X - предельная полезность товара X (в нашем случае мороженое);

∆TU_X - изменение в общей полезности товара X (удовольствие после первого, второго, … , двадцатого мороженого);

∆Q_X - изменение в количестве товара X, потребленного на протяжении периода (каждый раз вы ели только одно мороженое).

Для непрерывной функции полезности (вы ели мороженое порцию за порцией не прерываясь) предельная полезность определяется как наклон кривой функции полезности относительно некоторого уровня полезности. Она может измеряться в любой конкретной точке кривой, и равна первой производной функции в этой точке, т.е.

(0)

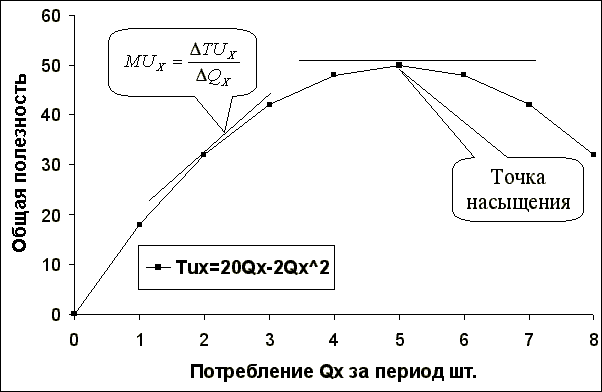
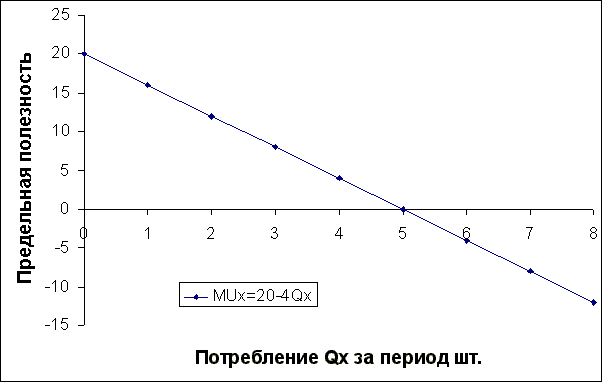
Рис. 1. Функции общей и предельной полезности

Графически первую производную функции в точке можно представить в виде касательной к данной точке. Вспомните доказательство площади круга S=πR².

Значения для TU_X и MU_X представлены на рис.1, на котором общая функция полезности представлена в верхней части, а соответствующая функция предельной полезности - в нижней части.

Рассмотрим подробней рис. 1. Если описать наши ощущения удовольствия, то они сначала росли быстро, но с каждой последующей порцией удовольствие уменьшалось, в какой-то момент времени оно стало нулевым, ну а дальше просто отрицательным.

Возникает вопрос, какая хорошо вам знакомая кривая лучше всего описывает эти ощущения? Правильно уравнение параболы, только перевернутой. При этом мы предполагаем, что вы достигли точки насыщения, когда съели пятую порцию и достигли 50 единиц общей полезности. Тогда функция полезности будет иметь вид TU=20Q_X-2Q²_X .

Это квадратичная функция, для которой предельная полезность является линейной функцией:

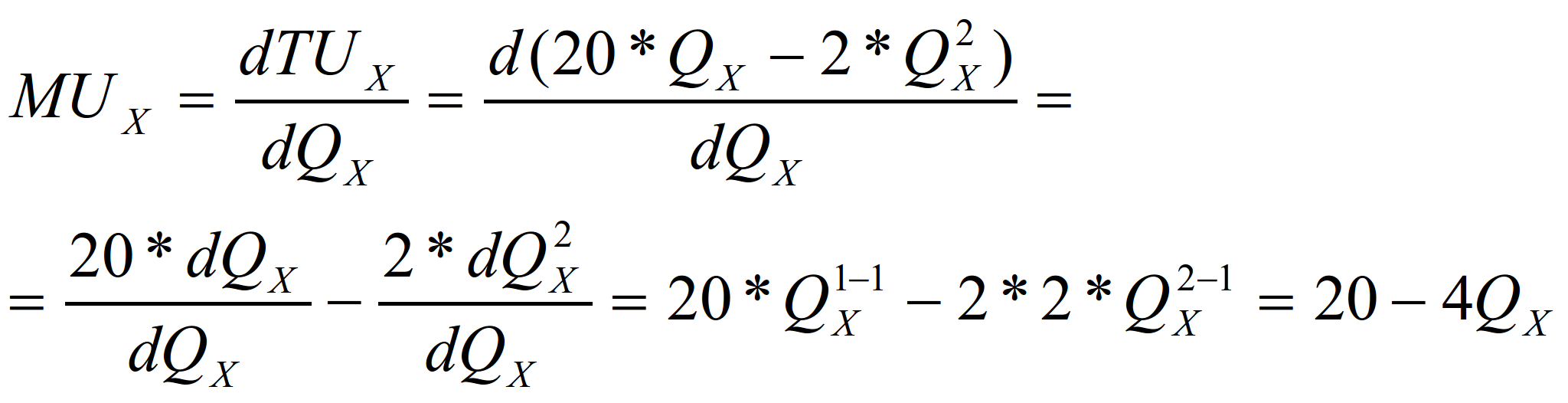
Поскольку предельная полезность представляет собой наклон кривой общей полезности, точка насыщения, в которой общая полезность является максимальной, легко определяется как точка, в которой предельная полезность равна нулю. Эта точка соответствует потреблению пяти единиц X за определенный период.

20-4Q_X=0,

Q_X=20/4=5

Если потребляется более пяти единиц, то устанавливается отрицательная предельная полезность, а общая полезность убывает.

Допущение убывающей предельной полезности является одним из основных понятий экономической теории.

Потребительское равновесие и максимальная полезность

Общий доход потребителя должен быть или израсходован, или сбережен в виде денег. Вопрос заключается в том, как потребитель решает, что именно покупать и сколько сберегать?

Предположим вы с друзьями решили выехать на природу на несколько дней, для этого вы идете в магазин, чтобы приобрести продукты, имея при себе 100 денежных единиц (у.е.), которые вы предполагаете все израсходовать. Потратите ли вы все на масло, все на свинину или все на хлеб? Вряд ли. Вы потратите какую-то сумму на масло, какую-то на хлеб, какую-то на свинину, какую-то на свежие овощи, какую-то на консервированную продукцию и т.д. Но при этом вы будете стремиться получить за свои деньги как можно больше удовольствия (товара).

Теперь давайте попытаемся создать модель поведения потребителя, которая предполагает этот же принцип здравого смысла – получить больше удовольствия (товара) за меньшие деньги.

При анализе поведения потребителя под максимальной полезностью будем понимать состояние равновесия.

Каждый закупленный продукт обеспечивает полезность, которая убывает по мере роста потребления, и каждый товар может быть закуплен по конкретной цене. Но как нам сравнивать относительную удовлетворенность, полученную от покупки товаров с несоизмеримыми ценами, такими, как цены на хлеб и цены на автомобиль. Для этого необходимо разделить предельную полезность этого товара на его цену MU_X/P_X. Полученное в результате соотношение представляет собой предельную полезность товара X в расчете на 1 условную единицу (у.е.).

Теперь предположим, что потребитель имеет фиксированную сумму денег, и всю ее он решил потратить на товар А и товар В. Если условная последняя единица денег, потраченная на А, обеспечивает более высокую предельную полезность, чем последняя единица денег, потраченная на В, то потребитель должен купить больше товара А и меньше В. Но по мере того, как потребляется больше товара А, их предельная полезность убывает. По мере того, как потребляется меньше товара В, их предельная полезность возрастает. В конечном счете, предельная полезность в расчете на 1 у.е. уравнивается и для товара А, и для товара В. В этой точке потребитель больше не может повышать общую полезность путем покупки большего или меньшего количества того или другого товара. Потребитель находится в состоянии равновесия, потому что:

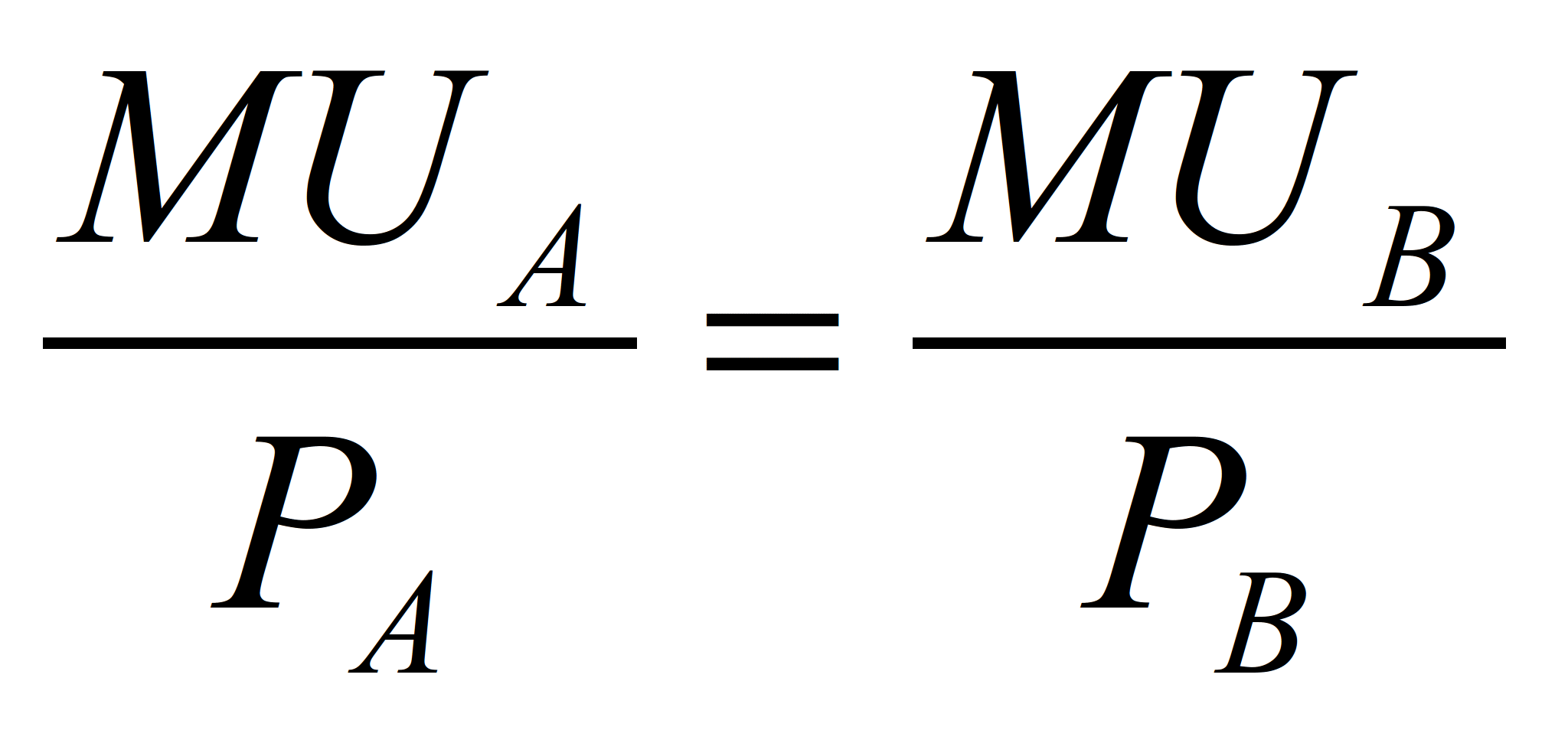
Та же самая процедура может быть использована для установления равновесия в потреблении множества товаров. Далее, рассматривая деньги как сэкономленный товар, цена которого всегда составляет 1 у.е. за 1 у.е., мы можем установить общее правило для состояния равновесия потребителя:

Потребитель достигает максимального уровня полезности в точке равновесия, в которой предельная полезность в расчете на последнюю потраченную 1 у.е. одинакова для всех товаров, включая деньги (MUM), т.е.

(0)

Это уравнение представляет собой модель полезности для максимизации удовлетворенности потребителя, включая удовлетворенность от экономии денег.

Таким образом, можно сказать, что потребитель достигает эффективности при покупке разных товаров посредством их уравнивания на предельном уровне и максимизации на общем уровне полезности.

Предельная полезность и кривые спроса

Кривая спроса потребителя может быть получена из данных по предельной полезности. Как мы уже видели, если потребитель находится в состоянии равновесия, то предельная полезность в расчете на 1 у.е. для любого конкретного товара равна предельной полезности денег, т. е.

(0)

где MU_M - предельная полезность денег;

MU_X - предельная полезность товара X;

P_X - цена единицы товара X.

Перекрестное умножение дает:

(0)

Отсюда

(0)

Предположим, что предельная полезность денег является постоянной, скажем, MU_M=2, а предельная полезность товара X равна MU_X=200-4Q_X. Используя эту информацию наряду с уравнением (6), мы получим данные, представленные в табл. 1.

Таблица 1. Расчет цены на базе информации по предельной полезности товара X и предельной полезности денег

Если количество, Q_X, и цену, P_X, представить графически, то результатом явится кривая линейного спроса, представленная на рис. 2.

Направленный вниз наклон кривой спроса является прямым результатом закона убывающей предельной полезности. Если потребленное количество увеличивается на одну единицу, то предельная полезность снижается, если даже общая полезность и будет возрастать. Потребитель не хочет обменивать ту же самую сумму денег на дополнительную единицу, которая имеет более низкую полезность. Поэтому цена должна падать, если нужен рост потребления. В случае с индивидуальным потребителем необязательно следует, что если цена снижается, то потребление должно расти. Например, если вы купили новый компьютер или автомобиль, то вряд ли вы броситесь покупать еще один, потому что цены снизилась. Однако на общем рынке, на котором рыночный спрос является совокупностью (суммой) спроса всех потребителей, снижение цены способно привлечь других покупателей, которые пока не успели купить компьютер или автомобиль.

Кривая рыночного спроса является мощным инструментом для производителей, позволяющим определить, что и в каком количестве необходимо производить.

Вопросы для повторения и обсуждения

• Наше решение о покупке базируется на двух соображениях … Продолжите фразу.
• Экономисты определяют полезность как … Продолжите фразу.
• Полезность имеет много источников и причин. Это происходит потому, что полезность является функцией … Продолжите фразу.
• Полезность - это не абсолютная величина. Она разная для каждого человека. Кроме того, даже для одного человека она меняется в зависимости от времени и места. Почему? Приведите примеры.
• Объясните закон убывающей предельной полезности.
• Предположим, что потребитель имеет фиксированную сумму денег, и всю ее он решил потратить на товар А и товар В. Приведите формулу и объясните, когда потребитель находится в состоянии равновесия?

Закон спроса

Ранее мы видели, что спрос создается поведением отдельных потребителей. Отдельные функции потребительского спроса отражают то количество конкретного товара, которое потребитель готов и способен закупать по определенной цене в пределах определенного диапазона цен в конкретное время и в конкретном месте, допуская, что все переменные спроса, кроме цены, сохраняются постоянными.

Функция рыночного спроса - это сумма всех функций потребительского спроса на данном рынке. Таким образом, индивидуальные количества, запрашиваемые по данной цене, объединяются для образования рыночного спроса на продукцию по этой цене.

Спрос на большую часть продукции находится под воздействием множества факторов, а не только цены.

Функция спроса устанавливает зависимость между требуемым количеством и всеми переменными, оказывающими воздействие на спрос.

Теоретически функцию рыночного спроса можно представить в виде уравнения:

Q_d=f(P | X₁, X₂,..., X_n) (0)

где Q_d - требуемое количество (спрос);

P - цена;

X₁, X₂,..., X_n - все другие факторы спроса, которые сохраняются постоянными, как это показано вертикальной линией в формуле.

При любом эмпирическом изучении спроса в первую очередь нам необходимо выявить независимые переменные P | X₁, X₂,..., X_n и их связь с зависимой переменной Q_d.

Например, модель спроса может иметь следующий вид:

Q_D= f (P, t, Tp, I, E, N, А, О), (0)

где Q_D - требуемое количество определенного товара (Y);

P - рыночная цена этого товара (X);

t - время (X);

Tp - вкусы и предпочтения потребителя (X);

I - уровень дохода потребителя, т.е. доход плюс кредит (X);

E - ожидаемые потребительские цены, доходы и доступность товара (X);

N - количество потенциальных потребителей (X);

А - реклама и продвижение продаж (X);

О - все другие факторы (X).

Количественный спрос и изменения в спросе

Вы должны осторожно подходить к различию между изменениями в требуемом количестве и изменениями в спросе.

Рис. 3. Изменения в требуемом количестве и изменения в спросе

Если цена меняется, а другие переменные остаются постоянными, то результатом является изменение в требуемом количестве, как это показано на рис. 3.

Снижение цены с P₁ до P₂ приводит к перемещению вдоль кривой спроса D₀ по мере того, как требуемое количество меняется от Q₁ до Q₂.

На рис. 3., также показан эффект изменения дохода по отношению к спросу на стандартную продукцию.

Стандартная, или нормальная, продукция определяется как продукция, потребление которой увеличивается по мере увеличения дохода, напротив, продукция худшего качества - это такая продукция, потребление которой уменьшается с увеличением дохода. На данном рисунке, начиная с кривой спроса D₀, увеличение дохода заставляет всю кривую смещаться в сторону D₁. Таким образом, все большее количество требуется при всех уровнях цен. И напротив, уменьшение дохода снижает требуемое количество также при всех уровнях цен, и кривая смещается в сторону D₂.

Именно таков смысл термина "изменение спроса".

В случае с продукцией худшего качества (товары Гиффена) увеличение дохода будет заставлять кривую спроса смещаться в противоположном направлении. Дело в том, что изменение дохода способствует смещению кривой спроса в том или ином направлении, в зависимости от типа товара.

Люди с ростом благосостояния имеют тенденцию сокращать или исключать из своего потребления низкокачественные товары. Всем хорошо известно, что во время кризисов (резкое падение доходов населения) выгодно торговать не сливочным маслом, а маргарином и т.д.

Более того, смещение кривой спроса может быть вызвано не только изменением дохода, но также и изменением любой переменной, исключая цену.

Каждый из факторов, приводящих к сдвигу (изменению) кривой спроса, отражает или прямую или обратную зависимость.

Рассмотрим модель спроса с целью выявления вида зависимости.

Рыночная цена (P) исследуемого товара имеет обратную зависимость по спросу, сдвига кривой не происходит, идет движение по кривой.

t - временной фактор; с ростом времени потребитель более критичен к покупкам и выбирает лучший товар, кривая спроса сдвигается вниз влево;

Вкусы и предпочтения потребителя (Tp) к исследуемому товару всегда формируют прямую зависимость. С ростом данного фактора кривая спроса сдвигается вправо вверх.

Уровень дохода потребителя (I) всегда формирует прямую зависимость. С ростом данного фактора (для нормальных товаров, услуг) кривая спроса сдвигается вправо вверх.

Ожидаемые потребительские цены, доходы и доступность товара (E). Если потребитель ожидает рост цен в будущем периоде, и/или рост будущих доходов, то он склонен приобретать больше товаров, формируя прямую зависимость. С ростом данного фактора кривая спроса сдвигается вправо вверх. С ростом доступности товара потребитель меньше приобретает его, формируя обратную зависимость. С ростом данного фактора кривая спроса сдвигается влево вниз. Объединение трех факторов в один сделано для упрощения записи функции.

Количество потенциальных потребителей (N), имеет прямую зависимость, т.к. чем больше ажиотаж вокруг исследуемого товара, тем выше спрос на него. С ростом данного фактора кривая спроса сдвигается вправо вверх.

Реклама и продвижение продаж (А), имеет прямую зависимость при условии, что она профессиональна и объективна, недаром говорят "реклама - двигатель прогресса". Потребитель склонен покупать знакомый товар, пользующийся "виртуальной" популярностью. С ростом рекламной компании кривая спроса сдвигается вправо вверх.

Все другие факторы (О). В зависимости от типа продукта количество влияющих факторов может быть очень большим. Например, на мировых рынках нефти на функцию спроса влияет более 20 укрупненных факторов, каждый из которых содержит ряд своих параметров.

Тесты.

1. Рыночная цена (P) исследуемого товара, при увеличении цены движение происходит:

   Вверх по кривой спроса от P0 к P1. Вниз по кривой спроса от P0 к P2. Кривая спроса сдвигается вверх от D0 к D1. Кривая спроса сдвигается вниз от D0 к D2. Движения нет. Необходима дополнительная информация.

2. t – время. При увеличении времени движение происходит:

   Вверх по кривой спроса от P0 к P1. Вниз по кривой спроса от P0 к P2. Кривая спроса сдвигается вверх от D0 к D1. Кривая спроса сдвигается вниз от D0 к D2. Движения нет. Необходима дополнительная информация.

3. Вкусы и предпочтения потребителя (Tp). При увеличении Tp движение происходит:

   Вверх по кривой спроса от P0 к P1. Вниз по кривой спроса от P0 к P2. Кривая спроса сдвигается вверх от D0 к D1. Кривая спроса сдвигается вниз от D0 к D2. Движения нет. Необходима дополнительная информация.

4. Уровень дохода потребителя (I). При увеличении I движение происходит:

   Вверх по кривой спроса от P0 к P1. Вниз по кривой спроса от P0 к P2. Кривая спроса сдвигается вверх от D0 к D1. Кривая спроса сдвигается вниз от D0 к D2. Движения нет. Необходима дополнительная информация.

5. Ожидаемые потребительские цены, доходы и доступность товара (E). При увеличении E движение происходит:

   Вверх по кривой спроса от P0 к P1. Вниз по кривой спроса от P0 к P2. Кривая спроса сдвигается вверх от D0 к D1. Кривая спроса сдвигается вниз от D0 к D2. Движения нет. Необходима дополнительная информация.

6. Количество потенциальных потребителей (N). При увеличении N движение происходит:

   Вверх по кривой спроса от P0 к P1. Вниз по кривой спроса от P0 к P2. Кривая спроса сдвигается вверх от D0 к D1. Кривая спроса сдвигается вниз от D0 к D2. Движения нет. Необходима дополнительная информация.

7. Реклама и продвижение продаж (А). При увеличении А движение происходит:

   Вверх по кривой спроса от P0 к P1. Вниз по кривой спроса от P0 к P2. Кривая спроса сдвигается вверх от D0 к D1. Кривая спроса сдвигается вниз от D0 к D2. Движения нет. Необходима дополнительная информация.

8. Все другие факторы (О). При увеличении О движение происходит:

Закон предложения

В отличие от спроса предложение отражает другую сторону рыночных отношений - поступление товаров на рынок, которые производят производители. Процесс купли-продажи здесь рассматривается с позиции производителя (продавца) товара. Предложение характеризует, таким образом, готовность продавца продать определенное количество того или иного товара в определенный период времени (рис. 4.).

Рис. 4. Изменения в требуемом количестве и изменения в предложении

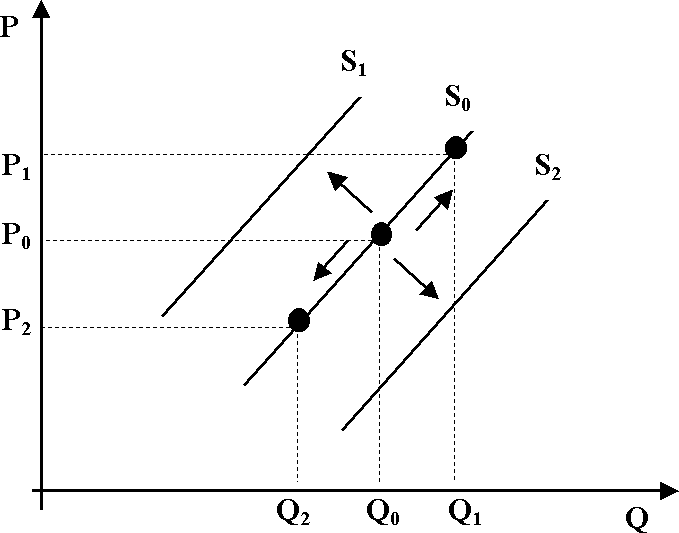
Минимальная цена, по которой продавец согласен продать определенное количество данного товара, называется ценой предложения. Здесь также имеет место зависимость количества предложения Q_i^S соответствующего товара в единицу времени от определенной совокупности факторов:

Q_i^S = f(P_i(+), P₁…P _i-1(+), t₍₊₎, L₁…L_m(-),T₍₊₎ , N_(-) , C₍₊₎ , Е_(-) , Z₍₊₎, O), (0)

где

плюс или минус отражают прямую или обратную зависимость влияния факторов.

P_i(+)- цена за единицу i-го товара; с ↑ (ростом) цен объем производства  (прямая зависимость), сдвига кривой не происходит;

P₁…P_i-1(+) - цены других товаров; с ↑ цен на другие товары объем производства  (прямая зависимость);

t₍₊₎ - временной фактор; с ↑ времени ↑ объем производства (прямая зависимость), кривая предложения сдвигается вниз вправо;

L₁…L_m(-) - производственные факторы (ресурсы); с ↑ цен на ресурсы объем производства ↓ (снижение) (обратная зависимость), кривая предложения сдвигается вверх влево;

T₍₊₎ - уровень применяемой технологии. Под технологией понимается набор известных способов или методов производства любого конкретного товара или вида услуг. С улучшением технологии, затраты на производство падают, т.к. уменьшаются привлекаемые ресурсы, объем производства ↑ (прямая зависимость), кривая предложения сдвигается вниз вправо. Например, с применением компьютерных технологий можно сократить персонал, т.е. уменьшается зарплата и связанные с ней налоги и социальные выплаты.

N_(-) - налоги и дотации; с ↑ налогов затраты на производство ↑, объем производства ↓, (обратная зависимость), кривая предложения сдвигается вверх влево;

C₍₊₎ - цели производства; с ↑ количества видов выпускаемой продукции риски  и банки готовы выдавать кредиты по более низким процентным ставкам, затраты на производство ↓, объем производства ↑, (прямая зависимость), кривая предложения сдвигается вниз вправо;

E_(-) - ожидания изменения цен; с ожиданием ↑ цен, объем производства ↓, (обратная зависимость), кривая предложения сдвигается вверх влево;

Z₍₊₎ - количество производителей; с ↑ количества производителей, цены на товары ↓, объем производства ↑, (прямая зависимость), кривая предложения сдвигается вниз вправо;

О - все другие факторы. В зависимости от типа продукта количество влияющих факторов может быть очень большим.

Если все эти факторы, определяющие объем предложения, кроме цены интересующего нас товара P_i, принять неизменными, то можно значительно упростить анализ, перейдя к функции предложения, характеризующей зависимость объема предложения товара только от его цены:

Q_i^S = f(P_i(+)). (0)

Как и функция спроса, функция предложения может быть представлена табличным, аналитическим и графическим способами. Очевидно, что в данном случае связь между ценой и количеством предлагаемого продукта является прямой.

С повышением цены соответственно возрастает объем предложения; со снижением цены объем предложения сокращается. Эта специфическая связь и носит название закон предложения.

Закон предложения показывает, что производители хотят изготовить и предложить к продаже большее количество своего продукта по высокой цене, чем они хотели бы это сделать по низкой цене.

Как и при рассмотрении спроса, следует различать изменение объема предложения и изменение предложения.

Изменение объема величины предложения означает передвижение с одной точки на другую на постоянной кривой предложения. Причиной такого передвижения является изменение цены на соответствующий товар.

Изменение предложения выражается в смещении всей кривой предложения. Увеличение предложения смещает кривую вправо, уменьшение предложения – влево, так как изменяется объем выпуска продукции.

Увеличение предложения (сдвиг линии предложения вправо) может произойти по следующим причинам:

1. Понижение цен на другие товары.
2. Понижение цен на используемые при изготовлении данной продукции ресурсы.
3. Снижение налогов и/или увеличение льгот на используемые при изготовлении данной продукции ресурсы.
4. Улучшение технологии производства данного товара.
5. Уменьшение налога на данный товар или введение дотаций.
6. Повышение (расширение) значимости целевых установок.

7. Ожидание понижения цен на изготовляемые товары.

Тесты

1. Цена за единицу i-го товара P_i . При увеличении данного фактора движение происходит:

   Вверх по кривой предложения S0 от P0 к P1. Вниз по кривой предложения S0 от P0 к P2. Кривая предложения сдвигается вверх от S0 к S1. Кривая предложения сдвигается вниз от S0 к S2. Движения нет. Необходима дополнительная информация.

2. Цены других товаров P₁…P_i-1. При увеличении данного фактора движение происходит:

   Вверх по кривой предложения S0 от P0 к P1. Вниз по кривой предложения S0 от P0 к P2. Кривая предложения сдвигается вверх от S0 к S1. Кривая предложения сдвигается вниз от S0 к S2. Движения нет. Необходима дополнительная информация.

3. Временной фактор t. При увеличении данного фактора движение происходит:

   Вверх по кривой предложения S0 от P0 к P1. Вниз по кривой предложения S0 от P0 к P2. Кривая предложения сдвигается вверх от S0 к S1. Кривая предложения сдвигается вниз от S0 к S2. Движения нет. Необходима дополнительная информация.

4. Производственные факторы (ресурсы) L₁…L_m(-).При увеличении данного фактора движение происходит:

   Вверх по кривой предложения S0 от P0 к P1. Вниз по кривой предложения S0 от P0 к P2. Кривая предложения сдвигается вверх от S0 к S1. Кривая предложения сдвигается вниз от S0 к S2. Движения нет. Необходима дополнительная информация.

5. Уровень применяемой технологии T₍₊₎.С улучшением технологии движение происходит:

   Вверх по кривой предложения S0 от P0 к P1. Вниз по кривой предложения S0 от P0 к P2. Кривая предложения сдвигается вверх от S0 к S1. Кривая предложения сдвигается вниз от S0 к S2. Движения нет. Необходима дополнительная информация.

6. Налоги и дотации N_(-) . При увеличении данного фактора движение происходит:

   Вверх по кривой предложения S0 от P0 к P1. Вниз по кривой предложения S0 от P0 к P2. Кривая предложения сдвигается вверх от S0 к S1. Кривая предложения сдвигается вниз от S0 к S2. Движения нет. Необходима дополнительная информация.

7. Цели производства C₍₊₎.При увеличении данного фактора движение происходит:

   Вверх по кривой предложения S0 от P0 к P1. Вниз по кривой предложения S0 от P0 к P2. Кривая предложения сдвигается вверх от S0 к S1. Кривая предложения сдвигается вниз от S0 к S2. Движения нет. Необходима дополнительная информация.

8. Ожидания изменения цен E_(-).При увеличении данного фактора движение происходит:

   Вверх по кривой предложения S0 от P0 к P1. Вниз по кривой предложения S0 от P0 к P2. Кривая предложения сдвигается вверх от S0 к S1. Кривая предложения сдвигается вниз от S0 к S2. Движения нет. Необходима дополнительная информация.

9. Количество производителей Z₍₊₎.При увеличении данного фактора движение происходит:

   Вверх по кривой предложения S0 от P0 к P1. Вниз по кривой предложения S0 от P0 к P2. Кривая предложения сдвигается вверх от S0 к S1. Кривая предложения сдвигается вниз от S0 к S2. Движения нет. Необходима дополнительная информация.

10. Все другие факторы О. При увеличении данного фактора движение происходит:

Эластичность спроса и предложения

Необходимо знать не только зависимость влияния факторов на спрос и предложение, но главное определить, на сколько изменится спрос и предложение при изменении любого из факторов на определенную величину.

На эти вопросы можно ответить, если понять концепцию эластичности спроса и предложения.

Эластичность любой функции показывает: насколько процентов изменится зависимая переменная Y (спрос, предложение), если независимая переменная Х (независимые факторы) изменилась на 1%, при условии, что все другие независимые переменные остаются постоянными. Или насколько процентов изменится объем продаж, если цена изменилась на один процент.

Например, если коэффициент эластичности спроса по доходу для исследуемого товара (автомобилей) равен 3, и доход населения вырос на 1%, то спрос вырастет на 3%. Кривая спроса сдвигается вправо вверх. Кривая предложения: движение кривой спроса вдоль кривой предложения.

Общее уравнение для измерения ценовой эластичности имеет следующий вид:

, (0)

где ε_D - ценовая эластичность спроса в точке;

Q_X - количество продукта X, которое требуется;

P_X - цена продукта X (при условии, что все остальные переменные остаются постоянными).

Такая эластичность функции спроса в точке просто представляет собой скорость изменения, ΔQ_X/ΔP_X, умноженную на коэффициент, P_X/Q_X, который является коэффициентом приведения к ее единицам измерения, использованным в вычислении.

Имеются два типа измерения эластичности.

Первый - прямое измерение в конкретной точке с использованием формулы точечной эластичности.

Второй - измерение средней эластичности по дуге или сегменту кривой спроса с использованием формулы дуговой эластичности.

Практическое значение

Дуговая эластичность применима к большинству эмпирических измерений ценовой эластичности спроса. При разработке маркетингового раздела бизнес-плана применяется чаще всего дуговая эластичность.

Точечная эластичность

Точечная эластичность определяет эластичность в конкретной точке на кривой спроса. Определение эластичности, представленном в уравнении ниже, выражение ΔQ_X/ΔP_X, аппроксимирует наклон криволинейной функции спроса вблизи точки (P_X ,Q_X), если ΔP_X достаточно мала.

Если мы хотим иметь точный наклон в этой точке, то мы применяем некоторые другие вычисления и предполагаем, что ΔP_X стремится к нулю. Отсюда вытекает условие:

, (0)

которое служит определением производной dQ_X/dP_X – а это есть ничто иное (вспомним геометрию), как тангенс угла наклона касательной в точке (P_X ,Q_X). Следовательно, мы можем определить точечную эластичность как:

(0)

Пример

Рассмотрим функцию спроса Q_x=30-2P_x,

где Q_X - требуемое количество продукта X,

P_X - цена продукта X.

Какова ценовая эластичность в точке на кривой, спроса, где P_X=6?

Продифференцируем функцию Q_x=30-2P_x, т.е. вычислим производную от данной функции. Геометрический смысл производной это тангенс угла наклона касательной к точке (P_X ,Q_X), отсчитываемый от оси Q, в нашем случае это коэффициент при P_x = -2, т.к. если продифференцировать функцию спроса, то:

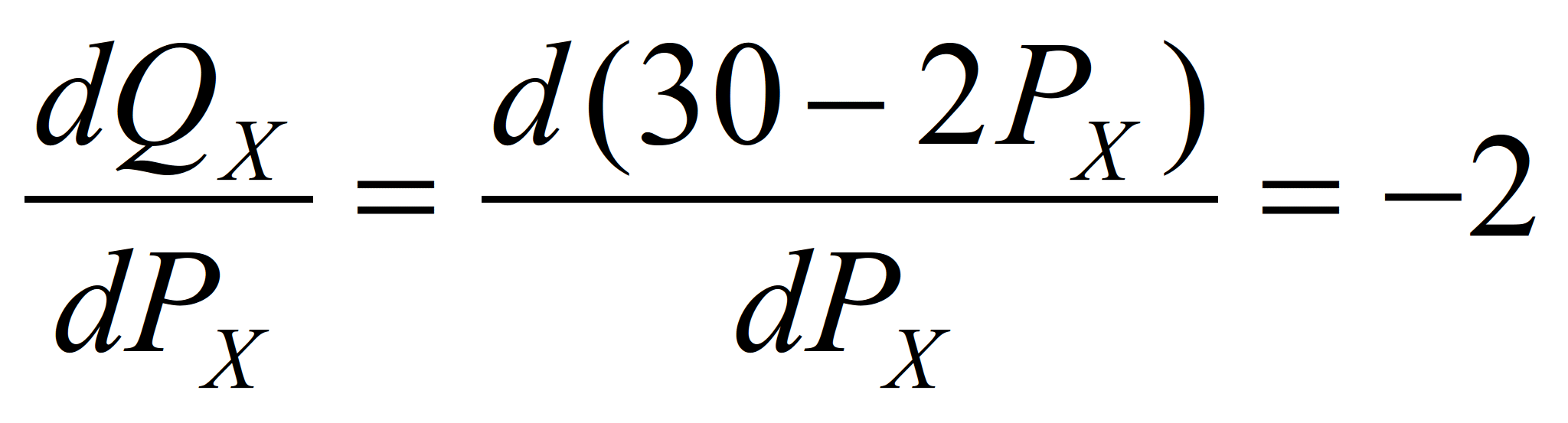
Если функция спроса линейна, то коэффициент при P_x и есть 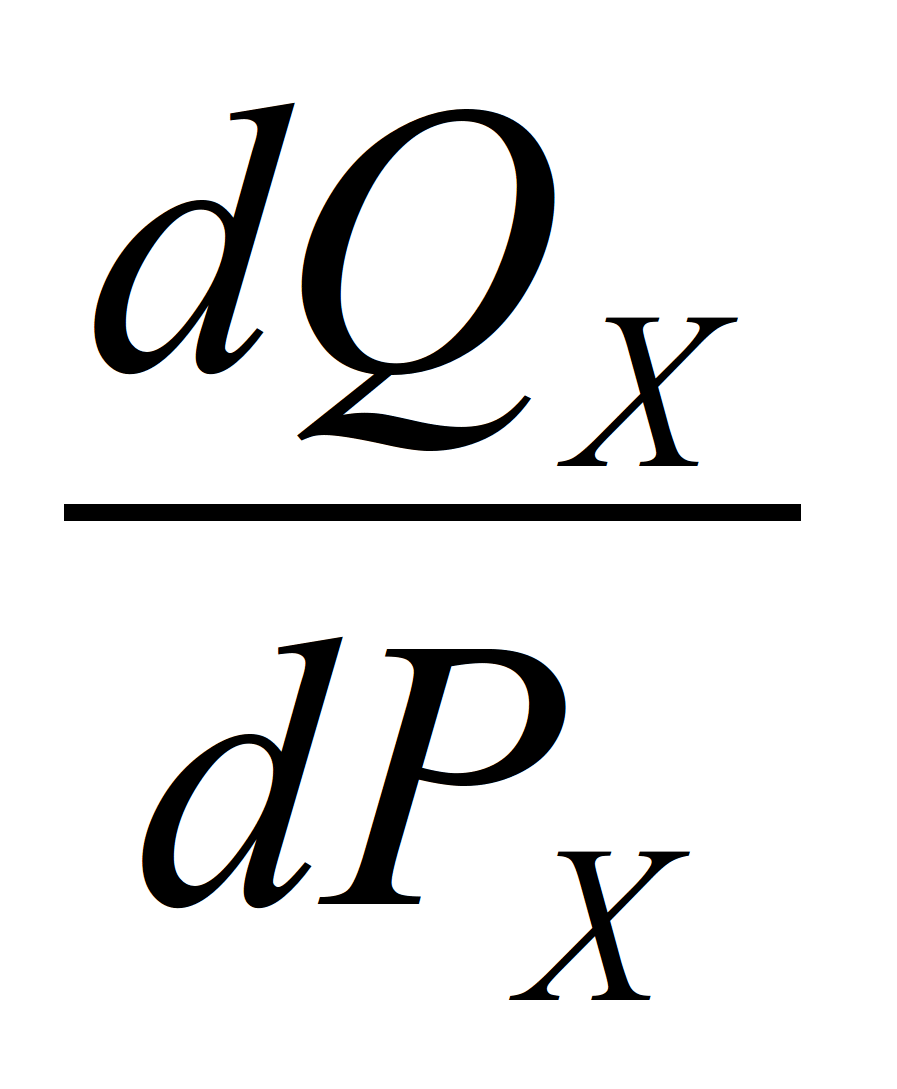. В нашем примере это "-2"

По уравнению (0) мы получаем:

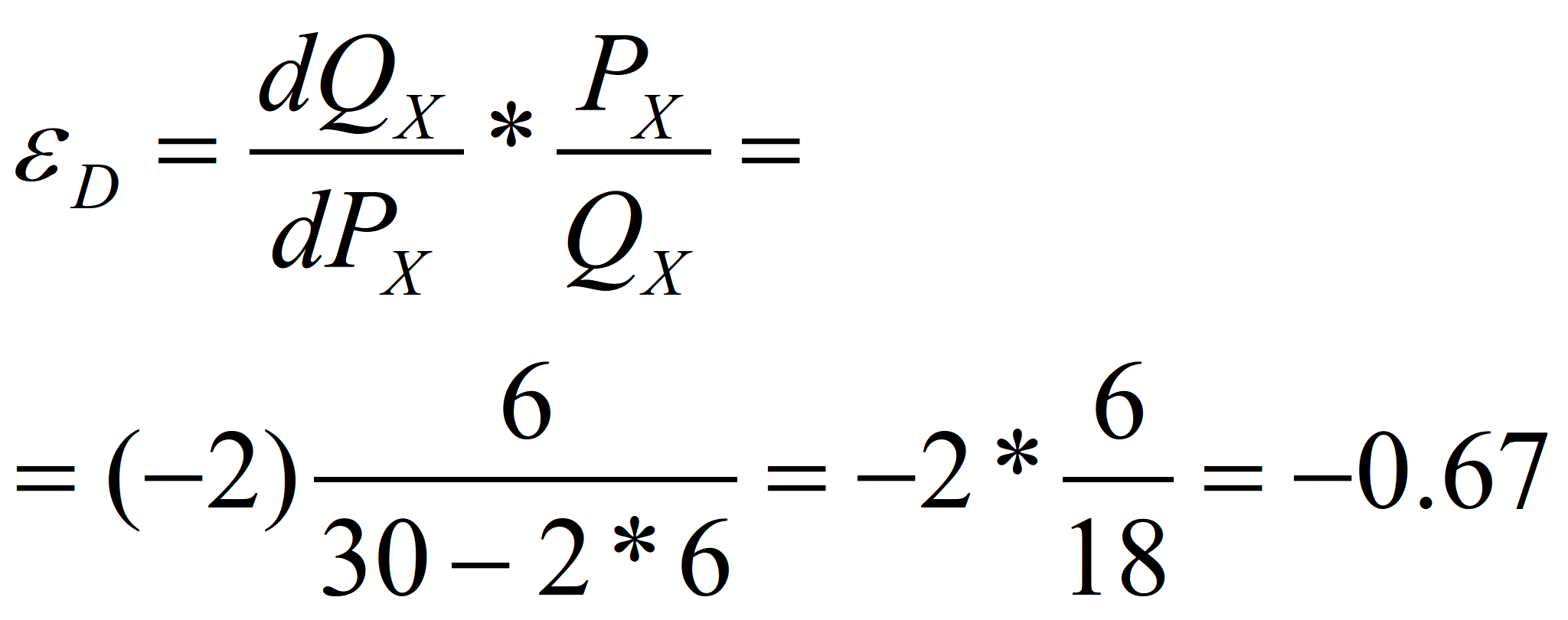
Это может означать, что если цена составляет 6 у.е., то изменение на 1% в цене может вызвать изменение на 0,67% в требуемом количестве. Знак "минус" означает, что переменные движутся в противоположном направлении.

Коэффициент эластичности для нормальных товаров, услуг всегда отрицательный, и как следствие наклон кривой спроса отрицательный, а для продукции худшего качества положительный, и как следствие наклон кривой спроса положительный.

Если кривая спроса линейная, то ее наклон постоянен, (dQ_X/dP_X)=(ΔQ_X/ΔP_X)=const. Отношение (P/Q) однако разное в каждой точке вдоль линии. Это отношение и определяет, что в любой точке линейной кривой спроса эластичность будет разной.

Эластичность различна в каждой точке на линии, независимо от того, является ли кривая линейной или нет.

Если имеется множество независимых переменных в функции спроса, то точка эластичности каждой переменной, X_i, может быть найдена с помощью частных производных, т.е. (ΔQ_X/ΔX_i)=(ΔQ_X/ΔX_i).

Если функция спроса линейная, то частные производные оказываются коэффициентами соответствующих переменных.

Примеры задач

Ваши фирмы производят различные товары, услуги. В результате исследования рынка вы получили линейную кривую спроса Q_D. Вы решили установить три варианта цен на свою продукцию в размере P₁, P₂, P₃. Рассчитайте эластичность при данной цене.

В таблице 2. выберете свой вариант функции спроса и цен, они даны в колонках Q_D и P₁, P₂, P₃. Проведите вычисления и полученные результаты сравните с ответами.

Вопросы:

1. Объясните, что определяет отрицательную эластичность, или положительную?
2. Почему эластичность в разных точках кривой спроса различна, даже если кривая спроса - линейная функция?

3. Какой множитель в формуле эластичности создает данный эффект?

Дуговая эластичность

Как уже говорилось ранее, точечная формула уравнения (0) отражает предельную концепцию и она действительна лишь для небольших передвижений от точки к точке вдоль кривой спроса. Более того, из уравнения (0) следует, что необходимо знать точное изменение в Q_X, вызванное очень малым изменением в P_X, т.е. требуется, чтобы функция спроса была известна.

Однако имеется много случаев, когда нам нужно измерить эластичность, а функция спроса неизвестна. Чаще нас интересует более крупный сегмент кривой спроса. Для этого нам необходима формула дуговой эластичности, которая вычисляла бы среднюю эластичность между двумя точками на кривой спроса.

Сущность формулы дуговой эластичности лучше рассмотреть на примере. Предположим, что цена яблока в супермаркете "Василек" в г. Нью Васюки снизилась с 50 у.е. за кг. до 38 у.е. за кг., вследствие чего средние продажи яблок увеличились с 300 до 450 кг. в день, что наглядно показано в таблице.

Эти данные определяют две точки вдоль кривой спроса, уравнения для которых мы не составили. Какова средняя эластичность между этими двумя точками? Если мы возьмем верхнюю точку (50, 300) за нашу базовую точку, то

Если мы используем нижнюю точку (38, 540) в качестве нашей базовой точки и будем перемещаться по кривой, то

Теперь мы видим, что ценовая эластичность яблок различна в верхнем и нижнем концах этого сегмента кривой спроса.

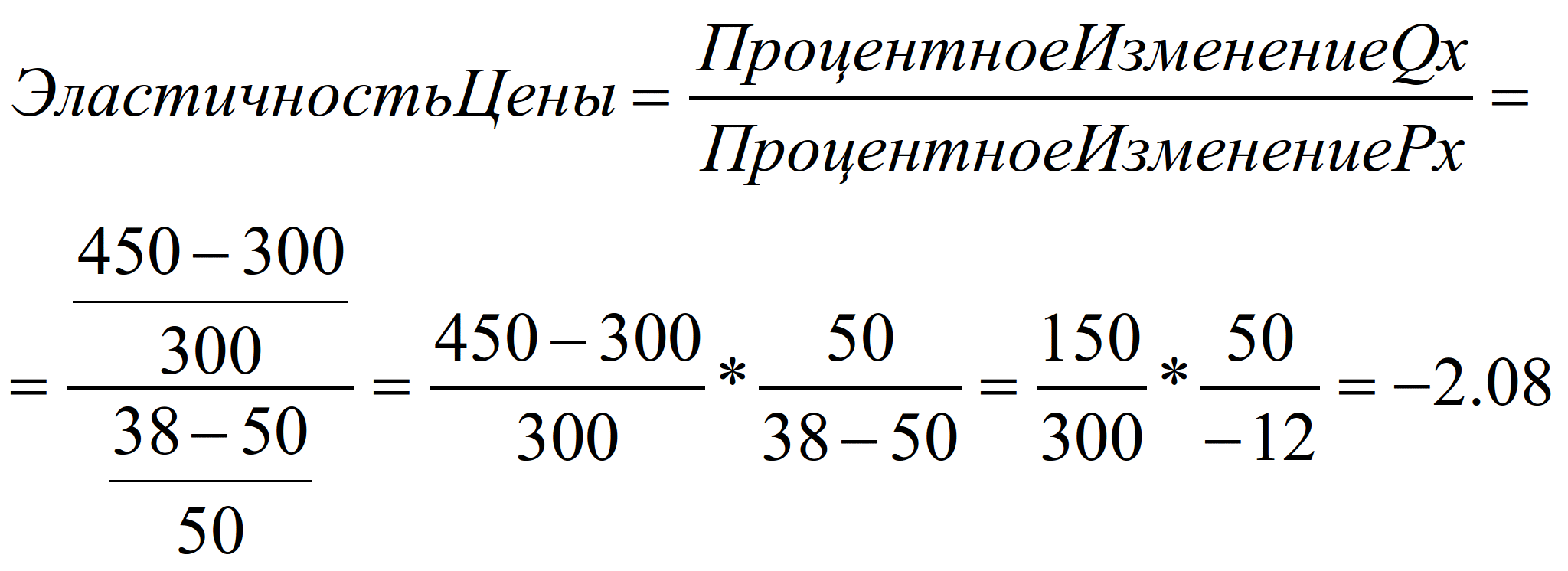
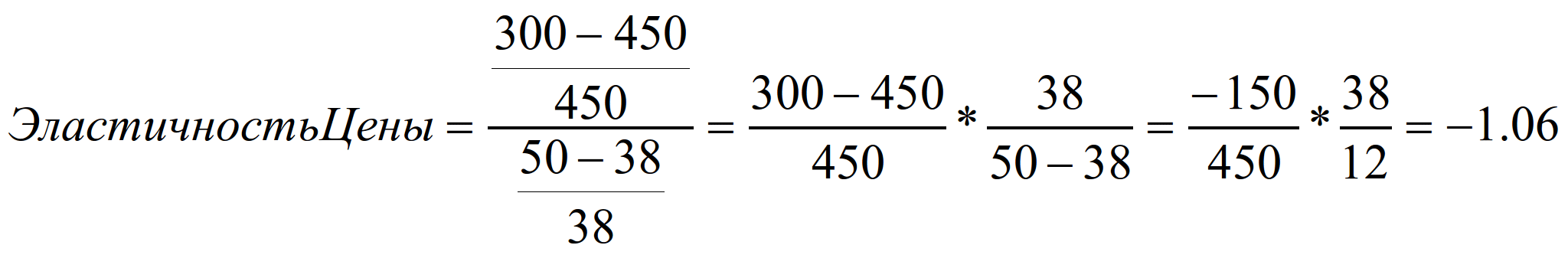
Что делать? Решение заключается в том, чтобы найти среднюю эластичность для данного приращения, меняющегося спроса. Для того чтобы сделать это, нам необходимо изменить базу для вычисления эластичности на среднее между двумя базами (P₁, Q₁) и (P₂, Q₂) на концах дуги. Средняя цена составляет (P₁+Р₂)/2, а среднее требуемое количество равно (Q₁+Q₂)/2. Эти средние координаты определяют точки на полпути между ними вдоль прямой линии. Затем мы модифицируем базисное определение эластичности, чтобы получить формулу дуговой эластичности с использованием средних координат P к Q. Изменения в P и Q - это изменения между конечными точками, т.е. ΔР=P₂-P₁ и ΔQ=Q₂-Q₁. Мы обозначаем дуговую эластичность как E_D, а не Δ_D, для того, чтобы отличить дуговую эластичность от точечной эластичности. Дуговая эластичность определяется следующим образом:

(0)

Применив формулу дуговой эластичности к нашему примеру, получим

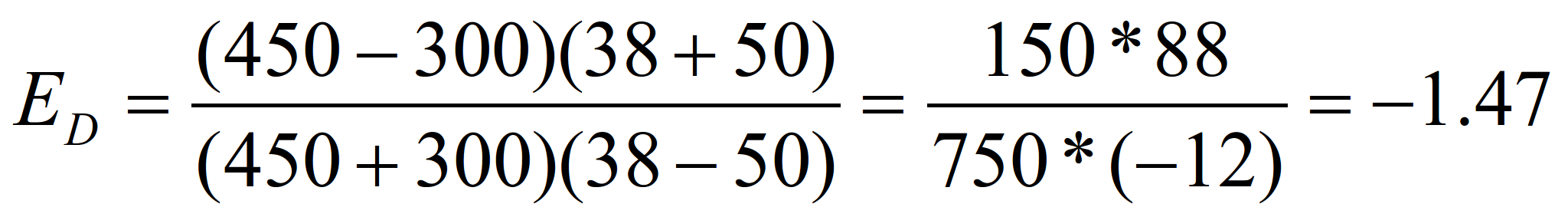
Это означает, что в среднем в пределах изменения цен от 50 до 38 у.е. за кг. при изменении цен на яблока на 1% требуемое количество будет меняться на 1,47%.

Пример

Допустим, что функция спроса равна Q_x=100-5P_x.

Вопросы

1. Какова ценовая эластичность спроса в точке, в которой цена равна 5 у.е., если цена увеличивается до 7 у.е.?
2. Какова ценовая эластичность в точке, в которой цена составляет 7 у.е., если цена снижается до 5 у.е.?

3. Какова средняя эластичность между этими точками?

Решения

1. Если P_x = 5, то Q_x = 100 - 5(5) = 75.

Если P_x = 7, то Q_x = 100 - 5(7) = 65.

Эластичность в конечных точках дуги равна: в точке (5, 75)

в точке (7, 65)

2. Средняя эластичность вычисляется по формуле дуговой эластичности:

Предостережение. Средняя эластичность в средней точке дуги не является средней между эластичностями конечных точек, т.е.

Точная дуговая эластичность может быть получена только с использованием формулы дуговой эластичности.

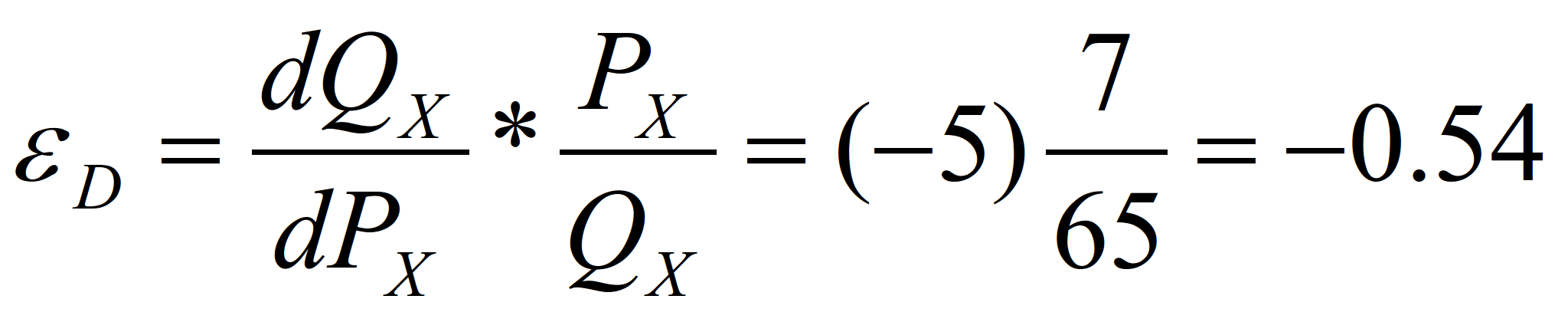
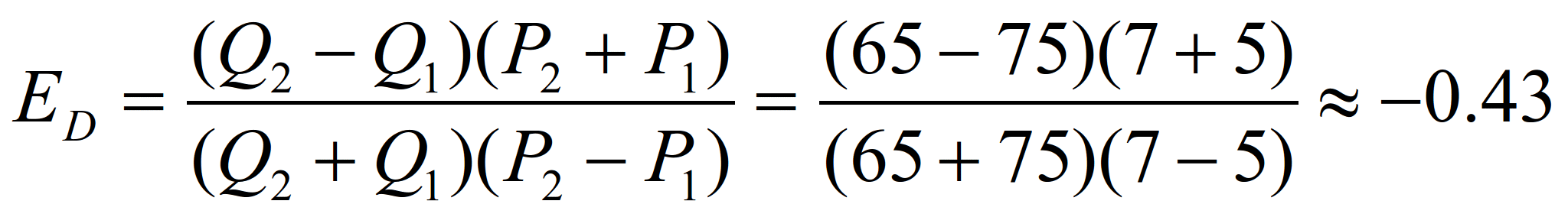
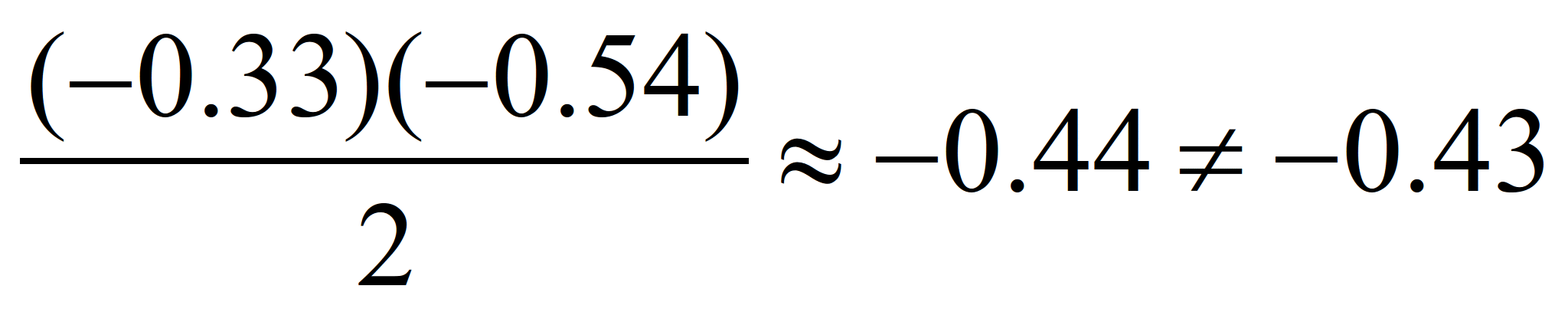
Задачи

Ваши фирмы производят различные товары, услуги. Для исследования рынка было решено изменить цены с P₁ до P₂. В результате изменился спрос на ваш товар с Q₁ до Q₂. Основная цель вашего исследования определить эластичность рынка в точках P₁, P₂, а также найти среднюю эластичность и дуговую эластичность. Кроме этого вы решили определить к какой группе товаров (нормальных, товаров Гиффена) рынок относит выпускаемый вами товар или услуги.

Простое напоминание. Когда товар нормальный - коэффициент эластичности отрицателен, когда товар низкого качества (Гиффена) – коэффициент эластичности положителен.

В таблице 3. выберете свой вариант P₁, P₂, Q₁, Q₂. Проведите вычисления и полученные результаты сравните с ответами.

Вопросы:

1. Если вам не известна функция спроса, какой коэффициент эластичности вы будете применять точечный или дуговой?
2. Какие коэффициенты эластичности точечные или дуговые проще получить при исследовании рынка?
3. Почему эластичность в разных точках (P₁, Q₁) и (P₂, Q₂) кривой спроса различна?
4. Эта особенность характерна для линейной или не линейной функций спроса?
5. Какой признак характеризует тип товара? Приведите примеры таких товаров.

Подведем итог:

• Точечная эластичность - это предельная концепция, потому что она измеряет эластичность в конкретной точке кривой спроса. Она может быть использована для анализа воздействий очень небольших изменений в цене.

• Более широкая концепция дуговой эластичности позволяет проводить измерения средней эластичности по более широкому диапазону изменений в цене. Дуговая эластичность, таким образом, более адекватный инструмент анализа эмпирических данных, касающихся цен и требуемых количеств.

Экономическая лаборатория. Построение уравнения спроса

Менеджеров кондитерской фабрики "АБ & Я" и сети магазинов интересует, как добиться максимального дохода. Для этого необходимо исследовать рынок города по 10 видам продукции, выпускаемой фабрикой и продаваемой в магазинах города. Они обратились к фирмам, специализирующимся на исследовании рынков, но цены за исследование слишком высоки для фабрики и сети магазинов. Они узнали, что вы прошли обучение прикладной экономике и способны по значительно более низким ценам выполнить эту работу.

Менеджеры фабрики предоставили перечень 10 видов продукции, подлежащих исследованию: 1 вид – карамельная конфета фабрики "АБ & Я" "Дюшес" и остальные 9 видов по списку, предоставленному фабрикой. В таблице эти виды продукции будем обозначать товар № 1, товар № 2, … , товар № 10.

Ваших заказчиков интересует объемы продаж в течение дня по каждому виду продукции.

Исследовать будем зависимость выручки от числа посетителей магазина:

Q^D_i= f_i (N_i, t, О), i=1,2,…,31

где Q_D – выручка i-вида продукции это произведение количества проданного товара на его цену;

N_i - количество покупателей i-вида продукции;

t – время исследования – в течение дня;

О - все другие факторы, которые не будут учтены в исследованиях.

Выручку (объем продаж) i-вида продукции будем измерять в рублях.

Для проведения исследования рынка вы случайным образом отбираете в своем микрорайоне или городе 15 магазинов.

Количество групп исследователей (регистраторов) должно соответствовать количеству магазинов – 15. Исследования начинаются в один день одновременно всеми группами.

Согласно условиям контракта с магазинами каждый продавец к концу дня должен подсчитать объем выручки по каждому виду исследуемого товара. И передать эти данные исследователям (регистраторам).

Все полученные данные должны быть сведены в таблицу.

В первую таблицу заносятся данные количества посетителей и выручка по каждому виду товаров. Для этого в колонку заносим данные по одному из 15 магазинов, а в строки зарегистрированные количество посетителей и выручку по каждому виду товаров.

Пример таблицы 4. приведен ниже.

На основе данных таблицы построим уравнение зависимости выручки от числа посетителей магазина для первого вида товара по всем 15 магазинам:

Q^D₁= f₁ (N₁, t, О)

Для этого по оси абсцисс (Х) будем откладывать значения количества посетителей в каждом магазине (N₁), и соответствующие им значения выручки (Q^D₁) - по оси Y. В результате получим множество точек на плоскости X0Y, которые мы видим на графике (см. рис. 5.). Расположение точек показывает, что существует взаимосвязь между X и Y, которую можно описать линейной функцией Y=kX+b.

Для этого возьмем линейку и нарисуем линию, проходящую между всеми точками – посередине. Чем больше мы бы выбрали магазинов, тем более точно была бы построена эта прямая. Далее найдем уравнение вычерченной прямой по выбранным произвольно двум точкам на ней.

Как вы помните уравнение прямой проходящей через две данные точки М₁(X₁,Y₁) и М₂(X₂,Y₂):

(Y-Y₁)/(Y₂-Y₁)=(X-X₁)/(X₂-X₁)

Ее угловой коэффициент:

k=(Y₂-Y₁)/(X₂-X₁)

Величина b получим из уравнения:

b=MY-kMX

Это уравнение требует пояснения. MY и MX – это средние величины. Их значения получаются суммированием Y и X и последующим делением на количество магазинов:

(0)

MX – это средняя величина посетителей. Эта величина получаются суммированием посетителей каждого из 15 магазинов и последующим делением на количество магазинов.

(0)

MY_k – это средняя величина выручки k-го товара. Эта величина получаются суммированием выручки k-го товара (в нашем случае товара №1), во всех 15 магазинах и последующим делением, полученной суммы на количество магазинов.

Вам также нужно рассчитать коэффициент эластичности. Для практических расчетов коэффициент эластичности равен:

, (0)

где 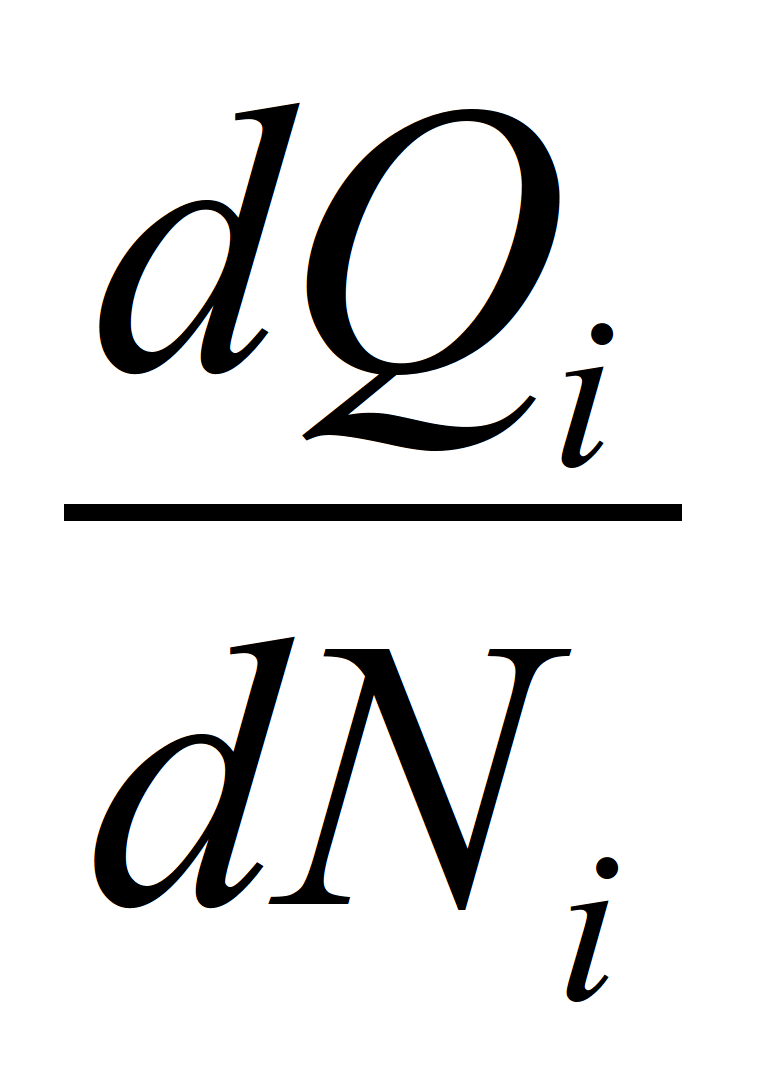- 1-я производная уравнения регрессии Y по X.

Все расчеты по 1 виду продукции сведены в таблицу 5. Рассчитайте все приведенные показатели по остальным 30 видам продукции и сравните с ответами.

Отметим очень важный момент. Величина b требует особого рассмотрения. Допустим, что количество посетителей Х=0, тем не менее, как видно из ответов, выручка будет существовать, что, по меньшей мере, вызывает удивление. Покупателей нет, а товар продается!? Кроме этого эта величина может быть как положительной, так и отрицательной. Так как же это можно экономически объяснить!? Да никак, такого быть не может!

Эта особенность объясняется очень просто.

С одной стороны, когда мы говорили о спросе, то сразу отметили, что это функция зависит одновременно от многих факторо:

Q^D_i = f_i (P, t, N_i, Tp_i, I_i, E_i, A_i, О),

а рассматриваем только один - количество посетителей N_i.

С другой стороны, если бы мы рассматривали все торговые точки (магазины, ларьки, палатки и т.д.) города, а не выбранные 15, вы бы получили более точную функциональную зависимость, но тогда затраты на исследование были бы огромны.

С третьей, вы не можете быть уверены, что все посетители были учтены, и кто-то из ваших коллег не ошибся!?

Этот перечень наших допущений можно продолжить.

Одним словом, параметр b это ошибка, которая учитывает все выше приведенные ограничения и допущения. Он не имеет никакого экономического смысла. В проведенных исследованиях нам было важно получить коэффициент эластичности.

В уравнении Q^D_i= f_i (N_i, t, О) ошибка определяется параметром О – все другие факторы, которые не были учтены в исследованиях.

Подобным образом мы могли бы исследовать более сложные модели спроса, например, приводимую выше модель:

Q^D_i = f_i (P, t, N_i, Tp_i, I_i, E_i, A_i, О),

Ответы в таблице были получены с помощью ПО "Инвест". Графические методы, которые мы применяли при определении коэффициента k, не обеспечивают такой степени точности. Тем не менее, ваши ответы должны быть близкими табличным и должны удовлетворить заказчиков.