
В методике используется база данных на примере 30 предприятий. Анализ проводится по каждому фактору в отдельности. В результате на графике, например, себестоимости, видны 30 точек этих организаций. При этом только одна точка на графике выделена жирно – это и есть исследуемое предприятие. После этого строится регрессионное уравнение. Данное уравнение представлено на графике в виде линии.

Рис.5. Модель коридоров управляемости зависимости показателя "себестоимость" от выручки. Средняя линия – регрессионное уравнение, показывающее средний уровень управления по данному показателю. Нижняя линия - регрессионное уравнение, показывающее лучший уровень управления по данному показателю. Верхняя линия - регрессионное уравнение, показывающее худший уровень управления по данному показателю.
Практически все облако 30 точек, лежащее на плоскости графика, делится этой средней линией на две группы – условно средне хорошо работающие организации в исследуемый период, и средне плохо работающие организации. Средняя линия, в нашем случае регрессионное уравнение является нормативом (среднеотраслевым, среднеподотраслевым, среднерыночным) исследуемого показателя для отобранных в выборку 30 организаций. Таким образом, осуществляется мгновенное зрительное разделение любой из 30-ти организаций на плохую или хорошую организацию. На этом этапе методика вводит категорию риска. Экономический смысл риска определяется просто. Хорошо работающие организации не будут рискованными по исследуемому фактору (например, по себестоимости) и наоборот плохо работающие организации будут нести в себе риски и в будущем потенциальные банкротства.
В методике оценка риска по одному исследуемому фактору проводится благодаря классификации (кластеризации, дискриминационному анализу и т.д.) по всем организациям, включенным в выборку. Подчеркнем, но только по данному фактору. Классификационный, кластерный, дискриминантный анализ провести не сложно благодаря рассчитанному регрессионному уравнению.
На следующем этапе определяется, где находится жирная точка – исследуемая организация, в зоне хороших или плохих организаций.
Понятно, что анализ можно проводить или в рамках производственной функции, когда, например, себестоимость является аргументом, или обратной ей теории затрат, когда себестоимость является функцией. В методике на данном этапе будет использоваться подход теории затрат.
Метод расчета риска прост – если исследуемый объект (его выделенная точка), например, показатель себестоимости, находится над уровнем функционального среднерыночного показателя, то затраты у исследуемой организации высоки по сравнению со средним показателем для организаций, включенных в выборку. Понятно, что высокие затраты по отношению к затратам конкурентов сигнализируют, что управление в исследуемой организации неэффективно, а раз неэффективно, то значит, рискованно. В этом случае организацию по исследуемому показателю можно отнести к организации, имеющей риски.

Рис.6. Модель коридоров управляемости зависимости показателя "кредиторская задолженность" от выручки. Средняя линия – регрессионное уравнение, показывающее средний уровень управления по данному показателю. Нижняя линия - регрессионное уравнение, показывающее лучший уровень управления по данному показателю. Верхняя линия - регрессионное уравнение, показывающее худший уровень управления по данному показателю.
Методика определяет меру риска такой организации в виде простого числа - 1, что характеризует наличие риска. Если исследуемый объект (его выделенная точка) находится ниже уровня функционального среднерыночного показателя, то методика определяет меру риска такой организации в виде простого числа - 0, что характеризует отсутствие риска. Как видно из предыдущего рисунка, по показателю "себестоимость" исследуемая организация малорискованная, т.к. выделенная точка находится ниже средней линии или регрессионного уравнения, т.е. себестоимость у нее ниже, чем в целом по рынку.
Данную организацию можно отнести к лучшим организациям, т.к. точка находится на пересечении с регрессионным уравнением по лучшим организациям. По каждому исследуемому фактору необходимо определить зону рисков или правило анализа рисков. Для приведенных 15 показателей правило оценки зоны риска следующее. Для прибыли, чистой прибыли, капиталу зона риска будет располагаться ниже средней линии, для себестоимости, и др. зона риска лежит выше средней линии. Модель коридоров управляемости зависимости показателя "кредиторская задолженность" от выручки дан на рис.6.
Пояснение для графиков и таблиц.
По оси 0Х – показатель выручка; по оси 0Y – например, показатель себестоимость.
Y=f(X) – функциональная регрессионная зависимость, среднерыночное значение доли любого из отобранных первичных факторов в выручке для конкурентной рыночной среды, результат в ед. или в %.
MX – среднерыночные значения или функциональная регрессионная зависимость доли исследуемого фактора в выручке для конкурентной рыночной среды, результат в %.
Мax – максимальные значения или функциональная регрессионная зависимость доли исследуемого фактора в выручке любого из отобранных первичных факторов в выручке для конкурентной рыночной среды, результат в %.
Min - минимальные значения или функциональная регрессионная зависимость доли исследуемого фактора в выручке любого из отобранных первичных факторов в выручке для конкурентной рыночной среды, результат в %.
Эконометрическая модель исследуемого показателя – регрессионная, среднеотраслевая зависимость исследуемого фактора (Y) от выручки (X), результат в ед. или в %.
Уровень управления в исследуемой организации, результат в %.
Риск – риск исследуемого объекта, его центра или центров ответственности по отношению к функциональной зависимости среднерыночных значений доли исследуемого фактора в выручке для конкурентной рыночной среды, результат (0/1).
Эффективность (убыточность, неэффективность) – потери исследуемого объекта в денежном выражении исследуемого объекта, его центра или центров ответственности по отношению к функциональной зависимости среднерыночных/среднелучших значений доли себестоимости в выручке в конкурентной региональной рыночной среде, результат в денежном выражении. Данный показатель в таблице представляется в виде:
Убыточность (неэффективность) исследуемой организации к среднелучшему показателю.
Общие положения методики для расчета интегральной эффективности/ущербов по активам и пассивам баланса организации.
1) Рост активов требует роста пассивов.
2) Рост пассивов требует увеличение займов у кредиторов (Поставщики, Персонал, Налоги, Кредиты).
3) Увеличение займов у кредиторов приводит к дополнительным процентным выплатам и снижению прибыли. За базу берем % банка.
Вывод для расчета ущерба/эффективности по активам по i-му фактору.
Ущерб = Σ((Аi - Aiср)*%Банка)
1) Аi - Исследуемое значение Активов i-го предприятия по i-му фактору, в денежном выражении.
2) Aiср - Среднерыночное/Отраслевое/Эталонное значение активов по i-му фактору, в денежном выражении.
3) %Банка - Процент за кредит/займ по банку, в %.
Методика требует рассматривать все процессы внутренней и внешней среды исследуемых организаций и их конкурентов по трем сценариям: лучший, средний, худший. В авторской методике по бизнес-планированию как подсистемы данной методики сценарные планы еще более ужесточаются. Так, в частности, три сценария учитывают определенную логику построения модели отчета о прибылях и убытках, как впрочем и по всем другим формам, сметам, моделям и т.д.:
1) При min реализации - max затрат = мin прибыли. Заведомо самый худший вариант сценария.
2) При max реализации - min затрат = мах прибыли. Заведомо самый лучший вариант сценария.
3) При mx реализации - mx затрат = средняя (мх) прибыль. Средний вариант сценария.
Следует обратить внимание, что MX - это среднее, но оно почти всегда будет иметь смещение или в сторону Мах, или в сторону Min. Это не среднеарифметическое и не средне взвешенное среднее это классическое треугольное вероятностное распределение, которое было описано в методике.
Данный момент очевиден. В авторских методиках бизнес-плана, а также анализа рисков, коридоров управляемости и эффективности исследуется минимум 10-20 тыс. факторов, показателей, в т.ч. интегральных. При этом рекомендуемая глубина исследуемых факторов по времени должна лежать в трехкратном диапазоне. Т.е. если бизнес-план строится/рассчитывается/моделируется на 5 лет вперед, то временной статистический анализ должен проводиться на глубину 5лет*3=15 предыдущих лет.
Эти требования к временной глубине статистической выборке должны выполняться и к методике анализа рисков, коридоров управления и эффективности и ко всем разрабатываемым эконометрическим моделям по всем рекомендуемыми авторами, минимум 25 математическим, статистическим, эконометрическим методам.
После расчета всех выше перечисленных показателей по каждому исследованному фактору они вносятся в таблицу для каждого фактора. Пример таблицы Ni (см. табл.2.), заполняемой по каждому из N исследуемых i-х факторов и его зависимость от объёма продаж в сравнении с эталонной моделью однородных конкурирующих организаций.
Таблица 2 - Анализ исследуемого фактора "Наименование фактора" исследуемой организации и его зависимость от объёма продаж в сравнении с эталонной моделью однородных конкурирующих организаций, например в млн.руб.
|
Наименование |
Величина |
|---|---|
|
Min – Среднеминимальное значение исследуемого показателя/фактора, % |
|
|
Max - Среднемаксимальная величина исследуемого показателя/фактора, % |
|
|
MX - Среднеотраслевая величина исследуемого показателя/фактора, % |
|
|
Эконометрическая (регрессионная, среднеотраслевая) модель исследуемого показателя, ед. или в % |
|
|
Уровень управления в исследуемой организации, % |
|
|
Риск показателя исследуемой организации (0/1) |
|
|
Убыточность (неэффективность) исследуемой организации к среднерыночному показателю, млн.руб. |
|
|
Убыточность (неэффективность) исследуемой организации к среднелучшему показателю, млн.руб. |
|
Предложенный алгоритм исследования каждого из факторов в методике демонстрирует простоту эконометрического анализа и позволяет сформировать коридоры управления, эффективности и рисков и выработать мероприятия по управлению всеми видами рисков.
Следует обратить внимание на то, что лучше использовать функциональную зависимость, а не средние оценки. Понятно, что функциональная зависимость точнее. Но для первого уровня анализа методика позволяет использовать средние оценки и признать линейность функциональных зависимостей. В методике такой уровень неточности для первого уровня анализа и оценки допустим.
В методике анализа рисков, эффективности, конкурентной позиции исследуемой организации по отношению к рыночной среде используются два подхода:
Экспертные оценки.
Традиционный подход это сбор первичной публичной статистической информации организаций и далее применяется многовариантный анализ, описанный ранее.
Экспертные оценки опираются, с одной стороны, на собранную первичную публичную статистическую информацию организаций, с другой стороны, на экспертные оценки, уточняющие, расширяющие первичные статистические данные. Экспертные оценки методика разрешает применять, если сбор статистических данных ограничен и традиционный подход невозможен. Необходимость экспертной оценки также возникает, когда количество исследуемых факторов/показателей в три раза больше, чем размер выборки исследуемых организаций. В этом случае экспертные оценки используются для статистического моделирования методом Монте-Карло, сплайн интерполяции, аппроксимации для формирования моделей нечетких множеств и нейронных сетей. В методике объем генерируемой выборки лежит в диапазонах 5-100 тыс. функционалов. После моделирования методом экспертных оценок применяется многовариантный анализ.
В методике предложена авторская простая идея, доступная для любого пользователя, статистического моделирования методом Монте-Карло, сплайн интерполяции, аппроксимации, моделей нечетких множеств, нейронных сетей.
На основании собранной первичной публичной статистической информации по отобранным организациям одной и той же отрасли (принцип однородности соблюден) эксперт, например, по каждому из 15-ти факторов должен/обязан решить - к какому из стандартных распределений каждый из 15-ти статистических факторов относится (Гаусса, Фишера, Стьюдента и т.д.). При этом эксперт должен учесть еще и все 5-ть глобальных ограничений акад. Колмогорова, которые невозможно обойти, не используя теорию размытых множеств.
В методике для решения данных ограничений Колмогорова предлагается следующий выход - расширить/объединить конструктивные подходы Колмогорова и теорию размытых множеств Заде.
Пример исходных экспертных оценок первичных факторов для статистического моделирования методом Монте-Карло, моделей нечетких множеств и нейронных сетей дан в табл. 3.
Таблица 3 Пример исходных экспертных оценок первичных факторов для статистического моделирования методом Монте-Карло, моделей нечетких множеств и нейронных сетей
|
Наименование |
Факторы |
Наклон |
Min |
Max |
|---|---|---|---|---|
|
Себестоимость |
Y1 |
67% |
25% |
25% |
|
Коммерческо-управленческие расходы |
Y2 |
14% |
20% |
20% |
|
Прибыль (убыток) до налогообложения Y3=X-Y1-Y2 |
Y3 |
|
|
|
|
Чистая прибыль Y4=Y3-Y3*Налог |
Y4 |
Налог,% |
|
|
|
Денежные средства |
Y5 |
5% |
30% |
30% |
|
Дебиторская задолженность |
Y6 |
17% |
33% |
33% |
|
Запасы |
Y7 |
10% |
35% |
35% |
|
Оборотные активы Y8=Y5+Y6+Y7 |
Y8 |
|
|
|
|
Внеоборотные Активы |
Y9 |
30% |
30% |
30% |
|
Активы Y10=Y8+Y9 |
Y10 |
|
|
|
|
Кредиторская задолженность |
Y11 |
21% |
25% |
25% |
|
Зарплата и Налоги |
Y12 |
12% |
21% |
21% |
|
Всего краткосрочные обязательства Y13=Y11+Y12 |
Y13 |
|
|
|
|
Долгосрочные и Краткосрочные обязательства |
Y14 |
10% |
29% |
29% |
|
Капитал и резервы Y15=Y10-Y13-14 |
Y15 |
|
|
|
Как видно из таблицы, экспертных оценок, в рамках подходов Колмогорова, Заде формируется треугольное вероятностное распределение по каждому из 15-ти интегрированных факторов публичной отчетности по отобранным организациям одной и той же отрасли.
Эксперт в процессе обработки статистических данных сосредотачивает свое внимание на треугольное распределение каждого фактора, состоящее как бы из трех вершин/точек: Минимальная величина/вершина, условно Средняя величина/вершина и Максимальная величина/вершина. Понятно, что треугольник (треугольное распределение) в экономике будет чаще ассиметричен (неравнобедренный), чем симметричен (равнобедренный).
Разобравшись с каждым фактором, с его треугольным вероятностным распределением, эксперт по методике формирует управляющую последовательность для дальнейшего статистического моделирования методом Монте-Карло, сплайн аппроксимации, моделей нечетких множеств и нейронных сетей. Размер генерируемой выборки должен быть минимум в 3-7 раз больше количества исследуемых первичных факторов, что позволяет учесть пять ограничений Колмогорова и использовать теорию размытых множеств Заде. После моделирования методом экспертных оценок далее применяется многовариантный анализ отраслевых, рыночных рисков, эффективности исследуемой группы организаций.
На следующем этапе методика требует проведения анализа отраслевых, рыночных рисков, эффективности исследуемой группы организаций на основе финансовых коэффициентов. На предыдущем этапе по первичным факторам рассчитаны эталонные среднеотраслевые/рыночные экономико-регрессионные уравнения/модели. На данном этапе при расчете любого представленного ниже финансового коэффициента необходимо использовать эти функциональные экономико-регрессионные уравнения/модели, просто подставляя их в формулу расчета конкретного финансового коэффициента.
Таблица 4 Модели расчета функциональных регрессионных зависимостей среднеотраслевых/среднерыночных финансовых коэффициентов (вторичных факторов)
|
Наименование первичных факторов |
Yi=KiX |
Наименование финансовых коэффициентов |
Регрессионная модель |
|
Себестоимость |
Y1 |
Текущая ликвидность |
CR=Y8/Y13 |
|
Коммерческо-управленческие расходы |
Y2 |
Быстрая ликвидность |
QR=(Y5+Y7)/Y13 |
|
Прибыль (убыток) до налогообложения |
Y3 |
Абсолютная ликвидность |
AR=Y5/Y13 |
|
Чистая прибыль |
Y4 |
Оборачиваемость запасов |
ITR=X/Y7 |
|
Денежные средства |
Y5 |
Оборачиваемость дебиторской задолженности в днях |
DSO=Y6/(X/360дн) |
|
Дебиторская задолженность |
Y6 |
Фондоотдача |
FAUR=X/Y9 |
|
Запасы |
Y7 |
Оборачиваемость активов |
TATR=X/Y10 |
|
Оборотные активы |
Y8 |
Доля заемных средств |
ДЗС=Y14/Y10 |
|
Внеоборотные Активы |
Y9 |
Рентабельность реализованной продукции |
NPM=Y4/X |
|
Активы |
Y10 |
Рентабельность продаж |
РП=Y3/X |
|
Кредиторская задолженность |
Y11 |
Рентабельность затрат |
РЗ=Y3/(Y1+Y2) |
|
Зарплата и Налоги |
Y12 |
Генерирование доходов |
BEP=Y3/Y10 |
|
Всего краткосрочные обязательства |
Y13 |
Рентабельности активов |
ROA=Y4/Y10 |
|
Долгосрочные и Краткосрочные обязательства |
Y14 |
Рентабельность собственного капитала |
ROE=Y4/Y15 |
|
Капитал и резервы |
Y15 |
Рентабельность основных средств |
РОС=Y4/Y9 |
Пример модели расчета функциональных регрессионных зависимостей среднеотраслевых/среднерыночных финансовых коэффициентов (вторичных факторов) дан в табл.4.
Пример расчета коэффициента "Текущая ликвидность". Чтобы вычислить коэффициент "Текущая ликвидность", необходимо разделить показатель "Оборотные активы" на показатель "Всего краткосрочные обязательства":
CR= Оборотные активы/Всего краткосрочные обязательства
Ранее при анализе первичных показателей были рассчитаны, построены эконометрические регрессионные зависимости показателя "Оборотные активы" (Y8) от выручки (X):
Y8= K8*X
И показателя "Всего краткосрочные обязательства" (Y13) от выручки (X):
Y13= K13*X
Исходные функциональные регрессионные зависимости показателя "Оборотные активы" (Y8) от выручки (X): Y8= K8*X и показателя "Всего краткосрочные обязательства" (Y13) от выручки (X): Y13= K13*X подставим в коэффициент "Текущая ликвидность" и получим:
CR=(K8*X)/(K13*X)
После сокращения в числителе и знаменателе выручки (X) получаем:
CR=(K8*X)/(K13*X)=K8/K13
Или как показано в таблице можно данный коэффициент представить в другом виде:
CR = (K8*X)/(K13*X) = K8/K13 = Y8/Y13
Графически регрессионные эконометрические функциональные уравнения лучших, худших и среднерыночных/среднеотраслевых показателей коэффициента "Текущая ликвидность" для наглядности представлены на рис.7.
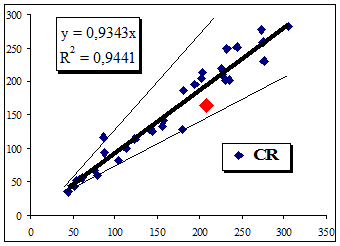
Рис.7. Графические регрессионные эконометрические функциональные уравнения лучших, худших и среднерыночных/среднеотраслевых показателей коэффициента "Текущая ликвидность"
Графически регрессионные эконометрические функциональные уравнения лучших, худших и среднерыночных/среднеотраслевых показателей коэффициента "Абсолютная ликвидность" для наглядности представлены на рис.8.

Рис.8. Графические регрессионные эконометрические функциональные уравнения лучших, худших и среднерыночных/среднеотраслевых показателей коэффициента "Абсолютная ликвидность"
Графически регрессионные эконометрические функциональные уравнения лучших, худших и среднерыночных/среднеотраслевых показателей коэффициента "Фондоотдача" для наглядности представлены на рис.9.

Рис.9. Графические регрессионные эконометрические функциональные уравнения лучших, худших и среднерыночных/среднеотраслевых показателей коэффициента "Фондоотдача"
Остальные коэффициенты, представленные в таблице, рассчитываются аналогично. Понятно, что количество коэффициентов (вторичных факторов/показателей) ничем не ограничено, кроме целей и задач конкретного исследования, при этом принцип расчета все равно сохраняется. Для этого достаточно определить конкретную формулу вычисления коэффициента (вторичного фактора) с единственным ограничением – можно ли описать этот коэффициент с помощью имеющихся первичных факторов. Чем больше первичных факторов будет исследоваться, тем большее количество коэффициентов (вторичных факторов) можно построить и рассчитать.
Пример построения нейронных моделей. Любому экономисту известно, что величина оборотных активов состоит из суммы денежные средства плюс запасы и дебиторская задолженность. Логика построения нейронной модели оборотных средств и всех трех перечисленных факторов аналогична за исключением того, что каждый из факторов включает в себя выборку исследуемых предприятий, которую можно представить в виде размытого облака точек организаций по конкретному показателю, например, запасы от выручки. Данную зависимость можно представить в виде регрессионного уравнения. В результате эти три исходных фактора, представленные в своих размытых плоскостях, если их проссумировать или проинтегрировать по всем поверхностям факторов и по всем точкам, то будет получен итоговый фактор оборотных активов. Это лингвистическое описание можно представить в виде нейронной модели (см.рис.).
Аналогичным образом можно построить нейронную модель активов, состоящую из оборотных средств и необоротных. При этом, если оборотные активы представить в виде ранее описанной нейронной модели, то будем наблюдать нейронную модель активов кА одноуровневую или двухуровневую. Если, в свою очередь, каждый из перечисленных показателей раскрыть, то мы будем иметь многоуровневую нейронную модель активов в виде дерева. Аналогичным образом можно описать пассивы бухгалтерского баланса. Увязать выручку и все факторы, определяющие выручку, построить нейронные модели, увязывающие форму 1,2 с формами 3.4.5. Кроме этого форма 1 и 2 имеют прямые и обратные связи, которые можно также описать с помощью нейронной модели.
Методика разработана авторами и описана еще в конце прошлого века. В книгах, учебных пособиях, монографиях авторов рассматривались, описывались теоретические, практические наиболее интересные моменты, в т.ч. алгоритмы и программные модули. Если сложить все публикации авторов с элементами настоящей методики с конца прошлого века, то можно сложить картину методики как пазлы. Для наглядности объединить их с видиолекциями в ютубе, будет понятна вся простота, скорость вычислений, объективность, многовариантность, качество методики рисков коридоров управления и эффективность и ее совместная работа с методикой по разработкой бизнес-плана организации.
В книге даны практические примеры исследований, сделанные на основе методики, по организациям различных отраслей:
Разработка бизнес-плана по мини пекарням.
Анализ рисков, коридоров управления и эффективности деятельности управляющих компаний СПб (ЖКХ).
Анализ рисков, коридоров управления и эффективности организаций нефтегазового комплекса.
Каждое исследование показывает, как использовать методику для организаций различных отраслей, как высвечивать проблемы организаций и решать их, используя различные целевые функции методики и меняя вектора исследований. В примерах применения методики показана особенность как даже в условиях ограниченного доступа к статистическим данным организаций можно эффективно ставить цели и решать задачи методики.