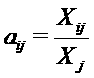 или в виде матрицы – А.
или в виде матрицы – А.Рассмотрим основные допущения, начальные и граничные условия и последовательность, алгоритм всех дальнейших расчетов динамической модели МОБ с учетом воспроизводства основных средств.
Вспомним, что для расчета коэффициентов прямых затрат для производства продукции j-й отрасли (колонки матрицы) необходимо разделить все внешние материальные затраты различных предприятий i-х (строки матрицы) отраслей Xij на объем продаж j-й отрасли Xj.
В результате получены коэффициенты аij
прямых затрат i-го продукта на единицу
j-го продукта, т.е. на его производство.
Данные расчеты представлены в виде
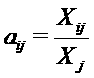 или в виде матрицы – А.
или в виде матрицы – А.
На следующем этапе построена модель МОБ с учетом воспроизводства основных средств.
Вначале обозначены все основные средства, используемые различными предприятиями одной отрасли как Фij. Соответственно, основные средства предприятий всех отраслей экономики можно представить в виде матрицы – Ф.
Для модели МОБ необходим не показатель фондоемкости (Ф=Ф/Х), а именно амортизационные отчисления на производство единицы продукции, т.е. величина амортизационных затрат. Понятно, что каждое здание, сооружение, оборудование, станок, компьютер и т.д. имеют свой индивидуальный срок службы. Обозначим средневзвешенный срок службы всех основных средств для предприятий каждой отрасли переменной Тij. В матричном виде данную переменную обозначим как - Т.
Предположим, что все предприятия, фирмы различных отраслей экономики применяют линейную модель амортизационных отчислений. В результате величину линейной амортизации можно представить в виде, т.е. разделим фондоемкость (Ф/Х) еще и на срок службы (Т) — получим амортизационные отчисления на производство единицы продукции:
В матричном виде амортизационные отчисления — B=Ф/(Х*Т).
Для того чтобы учесть все затраты, необходимо прибавить матрицу амортизационных отчислений (В) к матрице коэффициентов прямых затрат (А). В результате получим новую матрицу (А+В), в которой учитываются как прямые, так и амортизационные затраты.
Вычтя полученную матрицу А+В из единичной матрицы E, получим матрицу E-(A+В) — которая отражает величину добавленной стоимости в виде E-(A+В) без амортизационных отчислений В.
Далее обратив разность, получим новую матрицу коэффициентов полных затрат (E-A-B)-1 за вычетом амортизации.
Практически получена модель МОБ с учетом воспроизводства основных средств, естественно в рамках принятых допущений, начальных и граничных условий.
Безусловно, для того чтобы обеспечить рост экономики в следующих временных периодах, нужно обеспечить расширенное воспроизводство, а для этого необходимо обеспечить прирост не только основных (FОС) фондов (средств), но также предоставить предприятиям различных отраслей необходимые оборотные (FОБ) фонды.
Итак, для обеспечения расширенного воспроизводства необходимо определить величину всех элементов матрицы основных (FОС) фондов, а также величину элементов матрицы оборотных (FОБ) фондов. Просуммировав матрицы основных (FОС) фондов и оборотных (FОБ) фондов, получим необходимый объем приростных фондоемкостей:
На следующем этапе необходимо определить планируемые величины темпа роста экономики для предприятий каждой отрасли. Обозначим матрицу величин индивидуального темпа роста отраслей экономики в виде диагональной матрицы K. И рассчитаем прирост фондов по отраслям – данная величина это произведение матрицы объема приростных фондоемкостей (F) на матрицу темпа роста экономики для предприятий каждой отрасли (K):
Для того чтобы учесть все затраты необходимо к матрице коэффициентов прямых затрат А прибавить матрицу амортизационных отчислений – В, также прибавить матрицу прироста фондов по отраслям FK. В матричной записи данную величину можно показать в виде:
Учитывая, что в каждом временном этапе планируется произвести предприятиями каждой отрасли единицу «1» продукции, то необходимо определить, сколько затрат (A+B+FK) в каждой единице «1» продукции. Для этого достаточно из единичной (диагональной) матрицы вычесть матрицу затрат (A+B+FK). В матричной записи данную разницу можно изобразить в виде:
Далее обратив разность, получим новую матрицу коэффициентов полных затрат. В матричной записи данную величину можно представить в виде:
В ней учтены все затраты, матрица прямых затрат – А, матрица амортизации - B, и затраты прироста фондов по отраслям матрица - FK.
Рассчитав полные затраты с учетом всех существующих и планируемых затрат, можно определить реальную величину конечного потребления (спроса) или ВВП в текущем периоде. В матричной записи данную величину можно представить в виде:
В заключении отметим, что реальная величина конечного потребления (спроса) или ВВП в текущем периоде, когда учитывались только прямые затраты Y(E-A) будет больше ВВП, в котором учтены прямые и амортизационные затраты Y(E-A-B). В свою очередь, эта величина ВВП будет больше ВВП, в котором учтены прямые, амортизационные и затраты прироста фондов Y(Е-A-B-FK).
ЗАМЕЧАНИЕ. Для реализации международной программы сопоставления развития различных стран-членов ООН в системе национальных счетов СНС ООН в рамках МОБ предусмотрена единая классификация основных средств (Ф), и соответственно та же классификация по показателям: амортизации (В), сроку службы (Т), инвестициям (FK).
Понятно, что используя эту отчетность многие вычисления можно осуществлять более просто, исходя из имеющихся статистических таблиц или интернет баз данных.
Так, например, в интернет базах данных США эти массивы информации: основных средств (Ф), и соотвественно по амортизации (В), сроку службы (Т), инвестициям (FK) по основным секторам/отраслям, начиная с 1947г. по настоящий отчетный период, представлены достаточно подробно. Для этого достаточно посетить интернет источник бюро экономического анализа министерства торговли США и скачать базу данных – http://bea.gov/national/FA2004/Details/Index.html. На этом же сайте можно найти множество других показателей, счетов по национальной экономике США — http://bea.gov/national/index.htm, а также уже исходных, обработанных и готовых таблиц МОБ как в ценах потребителей, так и в ценах производителей — http://bea.gov/industry/io_annual.htm. Данные по персоналу (профессии, численность, оплата труда) рекомендуем уточнять на сайте бюро трудовой статистики министерства труда США — http://stats.bls.gov/oes/current/oessrci.htm.
В статической модели межотраслевого баланса (с учетом амортизации) продукция каждой отрасли распадается на две основные части:
Между тем часть последнего - конечный продукт, направляемый на расширение производства, в конечном счете, остается в сфере производства и, следовательно, как и фонд возмещения, не может быть самоцелью.
В руках общества для удовлетворения его потребностей остается лишь та часть конечного продукта (ВВП), которая не возвращается в сферу производства для ее расширения. Соотношение этих двух частей конечного продукта связано с темпами роста производства. Учет всего этого при построении межотраслевого баланса и означает переход от статической к динамической модели.
Как известно, рост производства может достигаться как введением в эксплуатацию новых фондов, так и улучшением использования уже действующих.
Для начала определим ряд понятий, которые нам необходимы для построения динамической модели межотраслевого баланса расширенного воспроизводства.
Простые моменты процесса труда — целесообразная деятельность, или самый труд, предмет труда и средства труда — образуют первичные элементы издержек производства. При повторении процесса труда (воспроизводстве) вещественные его элементы (средства производства) возмещаются (вычитаются) из общественного продукта. Сам труд не возмещается, он снова затрачивается, но предварительно должна быть восстановлена рабочая сила (работоспособность) человека. Средства существования, требующиеся для восстановления рабочей силы, представляют собой необходимый продукт. Издержки производства, сведённые к их вещественным элементам, представляют собой совокупные расходы материальных ресурсов (средств производства и средств существования для работников производства). Это общие черты издержек производства, вытекающие из простого процесса труда.
Конкретно-историческое содержание и формы издержек производства определяются уровнем развития производительных сил и специфическим характером условий воспроизводства совокупного продукта и рабочей силы, свойственных данному способу производства. Благодаря росту производительности труда на определённой ступени исторического развития человек получил возможность производить больше продуктов, чем было необходимо для возмещения потребленных средств производства и восстановления его рабочей силы.
Оборотные фонды (FОБ), часть производственных фондов организаций, которая целиком потребляется в каждом производственном цикле и полностью переносит (передаёт) свою стоимость на новый продукт труда. Оборотные фонды (FОБ) меняют свою натуральную форму в процессе производства, их стоимость в течение одного производственного цикла целиком входит в издержки (затраты) производства продукции.
В оборотные средства включают: денежные средства организации, используемые для создания производственных запасов сырья, материалов, топлива, тары, инструмента, производственного и бытового инвентаря; заделы незавершённого производства; запасы готовой продукции, а также средства, вложенные в расчёты и остатки денежных средств на расчётных счетах в банках и в кассах предприятий и организаций. Одна часть их функционирует в процессе производства, другая — в сфере обращения.
Оборотные фонды (FОБ) состоят из предметов труда — производственных запасов (сырья, основных и вспомогательных материалов, топлива, покупных полуфабрикатов и т.п.) и незавершённой продукции (полуфабрикатов собственного изготовления и расходов будущих лет, т.е. затрат на продукцию, которая будет выпущена в будущем). В стоимость незавершённой продукции включается зарплата рабочих и служащих, начисленная на выпуск этой продукции.
К оборотным фондам (FОБ) относятся также малоценные и быстроизнашивающиеся предметы и инструменты, стоимость которых не более установленной нормы или срок службы менее одного года (независимо от их стоимости). Функционирование предприятий связано с наличием определённых производственных запасов на всех стадиях воспроизводства. Они обеспечивают непрерывность и ритмичность всех производственных процессов и служат своего рода страховым резервом на всех стадиях общественного воспроизводства.
В то же время излишки производственных запасов замедляют оборот фондов, снижают эффективность производства, создают напряжённость в снабжении и т.д. Поэтому объём оборотных фондов народного хозяйства является одним из важнейших показателей, характеризующих экономический потенциал страны; скорость их оборота — показателем эффективности экономики ее технологического потенциала.
В то же время потребность в оборотных фондах возрастает в меньшей степени, чем выпуск продукции. Интенсификация производственных процессов, широкое развитие специализации и кооперирования предприятий, совершенствование материально-технического снабжения и транспортных процессов в народном хозяйстве (размеры, сроки и регулярность поставок), технико-экономическое обоснование норм запасов и расхода сырья, материалов и т.п. на изготовление продукции, сокращение отходов при обработке являются важным резервом повышения эффективности общественного производства.
Фонды основные (FОС) в экономике, совокупность производственных основных фондов предприятий и объединений и непроизводственных основных фондов.
Развитие общественного производства, повышение его эффективности связаны в значительной степени с более рациональным использованием фондов основных (FОС) как материально-технической основы всех отраслей народного хозяйства. Повышение уровня использования их непосредственно отражается в росте фондоотдачи.
В состав фонды основные (FОС) включаются основные фонды: государственных, кооперативных и общественных предприятий и организаций, колхозов, а также находящиеся у населения жилые дома, хозяйственные постройки, многолетние насаждения, рабочий и продуктивный скот.
Рассмотрим модель, в которой предполагается, что весь рост производства обеспечивается только увеличением фондов.
Чтобы в j-и отрасли обеспечить прирост производства на единицу продукции в год, требуется вложить в нее в качестве дополнительных фондов fij продукции i-й отрасли. Это так называемая «приростная фондоемкость» за счет i-го продукта.
Важно заметить, что она, вообще
говоря, отнюдь не равна фондоемкости
фij для действующих фондов.
Для того же, чтобы обеспечить прирост
конечной продукции j-и отрасли на
ΔXj, требуется вложить
продукции i-й отрасли (промежуточный
спрос) в размере fijΔXj.
Таким образом, для расширения производства
в разных отраслях требуется вложения
i-гo продукта
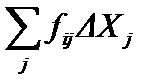 .
.
Эту величину
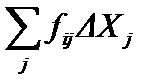 и надо взять из конечного продукта Yi
для обеспечения расширения производства
в разных отраслях.
и надо взять из конечного продукта Yi
для обеспечения расширения производства
в разных отраслях.
Величина конечного потребления
естественно будет уменьшена в текущем
году, т.к. для того чтобы в следующий год
обеспечить прирост производства, то
уже в этом текущем году необходимо
увеличить затраты на рост дополнительных
фондов fij продукции i-й
отрасли
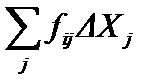 .
.
Подчеркнем, что этот рост должен быть осуществлен как по основным (FОС), так и по оборотным (FОБ) фондам.
Оставшаяся его часть, обозначим ее как Пi :
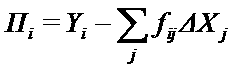
и образует то, что может быть использовано для удовлетворения потребностей общества (в широком смысле - для личного потребления, непроизводственной сферы, включая и оборону, и т.д.).
Уравнение баланса в результате получает вид:
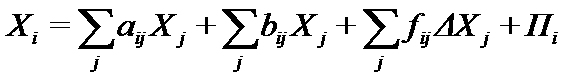
где fijΔXj есть прирост ΔФij фондов j-и отрасли за счет продукции i-й отрасли.
Здесь надо отметить, что коэффициенты fij учитывают необходимость вложения дополнительных средств не только в основные (FОС) фонды, но и в оборотные (FОБ).
В статической модели об этом речи не было: в ней оборотные фонды как бы «продвигаются» через процесс производства, превращаясь на его выходе в продукт, а возмещение материальных затрат их непрерывно на входе возобновляет.
Введем отраслевые темпы прироста производства kj.
Тогда, заменив ΔXj на kjXj, т.е. ΔXj=kjXj можем представить балансовое уравнение
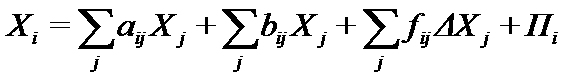
для i-го продукта в виде:
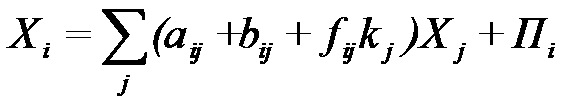
Чтобы написать систему этих уравнений в матричной форме, введем матрицу вновь вводимых фондов F коэффициентов fij и диагональную матрицу темпов прироста производства:
|
Темпы прироста производства
отраслей |
||||
|---|---|---|---|---|
|
k1 |
0 |
0 |
0 |
0 |
|
0 |
k2 |
0 |
0 |
0 |
|
0 |
0 |
k3 |
0 |
0 |
|
0 |
0 |
0 |
k4 |
0 |
|
0 |
0 |
0 |
0 |
k5 |
и вектор П из элементов Пi.
Тогда эту систему можно записать, как
Таким решением является вектор:
В частности, полагая, например, все kj, кроме одного, равными «0», а также и П равным «0», найдем, какой выпуск всех продуктов обеспечил прирост данной отрасли. Легко видеть, что H может рассматриваться и как частный случай H* при K=0, т.е. когда темп роста на следующий год не предполагается.
Матрица А+В+FK должна удовлетворять условию неотрицательности полученных на ее основе коэффициентов, образующих матрицу H*, подобно тому как А или А+В должны были приводить к неотрицательной матрицы H
Но теперь это условие означает возможность не только производства, но и заданных темпов его роста (без привлечения ресурсов извне – допустим из США). Очевидно, возможны случаи, когда H неотрицательны, a уже H* этому условию не удовлетворяют.
Поясним. Это вытекает из элементарного, ведь если из единичной матрицы «1» вычесть сначала матрицу А, а из полученного значения вычесть еще и матрицу В, а затем разделить «1» на полученное значение - H=(E-A-B)-1. Становится понятно, что чем меньше знаменатель, тем больший результат от деления. Т.е.
Экономический смысл (Е-A-B-FK)-1 можно определить следующим образом, чем больше величины, элементы матриц А, B, FK, тем сложнее технологии, выше уровень разделения труда, тем больше предприятий участвуют в производстве конечного продукта.
Например, в финансово-банковской системе или торговле по сравнению с промышленностью сельским хозяйством или строительством элементы матрицы А не велики, поэтому финансовая система, банки, торговля не в состоянии играть роль локомотивов экономики.
Хочется верить, что экономисты либерального толка, наконец-то, с этим разберутся, иначе человечество никогда не выйдет из регулярных финансовых, экономических, политических кризисов.
Продолжим уже использованный выше пример.
Пусть приростные фондоемкости для применяемого в качестве основного средства продукта образуют вектора:
для 1-го (0,067 0,01 0,011 0,001 0,007),
для 5-го (0,125 0,05 0,075 0,1 0,333).
Здесь некоторые составляющие больше соответствующих фондоемкостям фij, другие меньше, третьи совпадают с ними.
|
Основные фонды |
||||
|---|---|---|---|---|
|
0,067 |
0,010 |
0,011 |
0,001 |
0,007 |
|
0,133 |
0,500 |
0,125 |
0,200 |
0,486 |
|
0,060 |
0,033 |
0,533 |
0,113 |
0,070 |
|
0,010 |
0,001 |
0,011 |
0,140 |
0,007 |
|
0,125 |
0,050 |
0,075 |
0,100 |
0,333 |
Далее, учтем, что на единицу прироста требуются дополнительные оборотные средства, образующие матрицу:
|
Оборотные фонды |
||||
|---|---|---|---|---|
|
0,013 |
0,002 |
0,002 |
0,0002 |
0,001 |
|
0,027 |
0,100 |
0,025 |
0,040 |
0,097 |
|
0,012 |
0,007 |
0,107 |
0,023 |
0,014 |
|
0,002 |
0,000 |
0,002 |
0,028 |
0,001 |
|
0,025 |
0,010 |
0,015 |
0,020 |
0,067 |
Прибавив к каждому элементу матрицы оборотных фондов FОБ, приведенные выше элементы матрицы основных фондов FОС, получим окончательную суммарную матрицу приростных фондоемкостей:
|
Всего фондов |
||||
|---|---|---|---|---|
|
0,080 |
0,012 |
0,013 |
0,001 |
0,008 |
|
0,160 |
0,600 |
0,150 |
0,240 |
0,583 |
|
0,072 |
0,040 |
0,640 |
0,135 |
0,084 |
|
0,012 |
0,001 |
0,013 |
0,168 |
0,008 |
|
0,150 |
0,060 |
0,090 |
0,120 |
0,400 |
Введем относительные темпы роста по отраслям в виде вектора
т.е. темп прироста 1-й отрасли составит - 5%, темп прироста 2-й отрасли составит - 4%, темп прироста 3-й отрасли составит - 3% и т.д.
|
Темпы прироста отраслей |
||||
|---|---|---|---|---|
|
5,0% |
0 |
0 |
0 |
0 |
|
0 |
4,0% |
0 |
0 |
0 |
|
0 |
0 |
3,0% |
0 |
0 |
|
0 |
0 |
0 |
2,5% |
0 |
|
0 |
0 |
0 |
0 |
1,0% |
Умножив ресурс основных и оборотных фондов - fij, т.е. F=FОБ+FОС на эти темпы - K, получим матрицу F*K:
|
Прирост фондов по отраслям |
||||
|---|---|---|---|---|
|
0,004 |
0,0005 |
0,0004 |
0,00003 |
0,0001 |
|
0,008 |
0,024 |
0,005 |
0,006 |
0,006 |
|
0,004 |
0,002 |
0,019 |
0,003 |
0,001 |
|
0,001 |
0,00003 |
0,0004 |
0,0042 |
0,0001 |
|
0,008 |
0,002 |
0,003 |
0,003 |
0,004 |
fijΔXj есть прирост ΔФij фондов j-и отрасли из продукции i-й отрасли или FK.
Отсюда суммированием все матрицы A+В+FK получим суммарную матрицу (A+В+FK):
|
Матрица |
||||
|---|---|---|---|---|
|
0,22 |
0,01 |
0,06 |
0,004 |
0,01 |
|
0,04 |
0,08 |
0,02 |
0,06 |
0,07 |
|
0,14 |
0,30 |
0,42 |
0,03 |
0,08 |
|
0,09 |
0,02 |
0,02 |
0,16 |
0,05 |
|
0,14 |
0,22 |
0,18 |
0,12 |
0,22 |
Вычтя ее из единичной матрицы, получим матрицу (E-(A+В+FK):
|
Матрица |
||||
|---|---|---|---|---|
|
0,78 |
-0,01 |
-0,06 |
-0,004 |
-0,01 |
|
-0,04 |
0,92 |
-0,02 |
-0,06 |
-0,07 |
|
-0,14 |
-0,30 |
0,58 |
-0,03 |
-0,08 |
|
-0,09 |
-0,02 |
-0,02 |
0,84 |
-0,05 |
|
-0,14 |
-0,22 |
-0,18 |
-0,12 |
0,78 |
Далее обратив разность, получим матрицу полных затрат H*=(E-A-B-FK)-1:
|
Полные затраты |
||||
|---|---|---|---|---|
|
1,32 |
0,08 |
0,16 |
0,02 |
0,05 |
|
0,10 |
1,15 |
0,10 |
0,10 |
0,12 |
|
0,43 |
0,70 |
1,90 |
0,15 |
0,26 |
|
0,18 |
0,08 |
0,09 |
1,21 |
0,10 |
|
0,40 |
0,51 |
0,52 |
0,26 |
1,40 |
|
Контроль на «0» |
4,18 |
|||
Если умножим H* на вектор потребления П, получим производственную программу, обеспечившую это потребление, и одновременно данные темпы роста производства предприятий различных отраслей.
Из этого еще не следует, что при таких темпах роста будет сохранен или тем более увеличен фонд потребления в последующем.
Рассмотрим задачу в более узком виде.
Предположим, на следующие годы планируется одинаковый темп роста для всех отраслей, при этом отраслевая структура сохраняется постоянной, неизменной. Для выполнения этого условия положим все kj=k. Матрицу FK можем представить как умножение коэффициентов темпа роста отраслей - k на матрицу F.
На следующем этапе будем поэтапно увеличивать темп роста всех отраслей экономики, т.е. матрицу K. Цель данного увеличения матрицы K – определить, на каком этапе определитель матрицы (E-A-B-FK)-1 достигнет «0» или станет отрицательным.
Понятно, что с увеличением k выше некоторого значения определитель станет отрицательным, а с ним отрицательными становятся и все элементы матрицы H*. Это математическая интерпретация важного экономического положения.
При данных коэффициентах прямых затрат (аij), удельной амортизации (bij) и коэффициентах приростной фондоемкости (fij) всегда существует максимально возможный темп роста, при этом естественно имеется в виду одинаковый темп роста для всех отраслей, и этот рост обеспечивается с сохранением неизменной структуры производства каждой отрасли.
Напомним, что fijΔXj есть прирост ΔФij фондов j-и отрасли из продукции i-й отрасли.
В нашем примере предельный уровень будет равен 48,5%.
|
Полные затраты |
||||
|---|---|---|---|---|
|
67,9 |
87,6 |
111,5 |
51,3 |
80,3 |
|
303,9 |
400,8 |
507,9 |
234,3 |
366,4 |
|
556,8 |
732,3 |
932,7 |
429,0 |
670,6 |
|
61,0 |
80,0 |
101,7 |
48,1 |
73,3 |
|
378,3 |
497,3 |
632,3 |
291,6 |
457,0 |
|
Контроль на «0» |
5833,6 |
|||
Это важная характеристика всей совокупности коэффициентов прямых затрат материалов, удельной амортизации и приростной фондоемкости.
Положив в нашем примере k=0.486 (т. е. несколько больше предельного), имеем откорректированную матрицу A+В+FK:
|
Матрица |
||||
|---|---|---|---|---|
|
0,25 |
0,02 |
0,07 |
0,005 |
0,02 |
|
0,11 |
0,34 |
0,09 |
0,17 |
0,35 |
|
0,17 |
0,32 |
0,72 |
0,09 |
0,12 |
|
0,10 |
0,02 |
0,02 |
0,23 |
0,06 |
|
0,21 |
0,24 |
0,22 |
0,18 |
0,41 |
Вычтя матрицу A+В+FK из E и обратив разность, придем к матрице:
|
Полные затраты |
||||
|---|---|---|---|---|
|
-95,8 |
-127,7 |
-162,4 |
-74,9 |
-117,1 |
|
-443,4 |
-581,8 |
-741,8 |
-341,7 |
-534,1 |
|
-812,0 |
-1067,4 |
-1356,2 |
-626,1 |
-978,9 |
|
-88,5 |
-116,5 |
-148,2 |
-67,0 |
-106,8 |
|
-551,2 |
-724,8 |
-922,0 |
-424,9 |
-663,2 |
|
Контроль отрицательности Определителя |
-8509,7 |
|||
Таким образом, чтобы добиться отрицательных значений матрицы достаточно установить темп прироста производства 48,6% - выше, чем предельный рост 48,5%.
Отрицательная величина элементов полученной матрицы указывает на невозможность решения экономической задачи: обеспечить рост на 8% при данных коэффициентах.
Для близкого к предельному k=0,485 H* неотрицательна, т.е. теоретически такой темп возможен, но для его обеспечения необходимы огромные капиталовложения; например, h*14=51,3 и т. д.
|
Полные затраты |
||||
|---|---|---|---|---|
|
67,9 |
87,6 |
111,5 |
51,3 |
80,3 |
|
303,9 |
400,8 |
507,9 |
234,3 |
366,4 |
|
556,8 |
732,3 |
932,7 |
429,0 |
670,6 |
|
61,0 |
80,0 |
101,7 |
48,1 |
73,3 |
|
378,3 |
497,3 |
632,3 |
291,6 |
457,0 |
Более сложным является вопрос о предельно возможных темпах, если они различаются по отраслям, так как в этом случае такой предел существует не для отдельного темпа, а для всего их вектора. Можно при этом зафиксировать темпы для всех отраслей, кроме некоторой одной, и искать предел для темпа этой последней. Или, имея в виду наш пример, в одной отрасли задать темп, несколько превышающий установленный выше предел 48,5%, но компенсировать это заданием другой отрасли темпа, меньшего, чем 48,5%.
При задании темпов механизм превышения предела состоит в следующем. Для обеспечения заданного темпа в одних отраслях надо увеличить производственную программу других. Но, так как для этих других темп задан, это увеличение приведет к увеличению и их прироста, а оно потребует увеличения производственной программы ряда отраслей. Последнее будет означать и увеличение прироста их продукции, поскольку этот прирост задан в виде темпа, и т. д. Иное дело, казалось бы, если рассматривать рост в виде абсолютных приращений ΔXj. Определив обеспечивающие их дополнительные фонды, эти фонды можно включить в конечный продукт и далее решать задачу по статической модели. В результате действительно получим вектор валовых выпусков, обеспечивающих возмещение затрат вместе с дополнительными вложениями в фонды. Так, в предыдущих примерах при рассмотренных темпах:
|
Темпы прироста отраслей |
||||
|---|---|---|---|---|
|
5,0% |
0 |
0 |
0 |
0 |
|
0 |
4,0% |
0 |
0 |
0 |
|
0 |
0 |
3,0% |
0 |
0 |
|
0 |
0 |
0 |
2,5% |
0 |
|
0 |
0 |
0 |
0 |
1,0% |
вектор валовых выпусков, обеспечивающих возмещение затрат вместе с дополнительными вложениями в фонды соответствует приращениям:
|
ΔX' |
19,8 |
27,2 |
87,0 |
41,4 |
51,4 |
|---|
Умножив на них приростные фондоемкости:
|
Всего фондов |
||||
|---|---|---|---|---|
|
0,080 |
0,012 |
0,013 |
0,001 |
0,008 |
|
0,160 |
0,600 |
0,150 |
0,240 |
0,583 |
|
0,072 |
0,040 |
0,640 |
0,135 |
0,084 |
|
0,012 |
0,001 |
0,013 |
0,168 |
0,008 |
|
0,150 |
0,060 |
0,090 |
0,120 |
0,400 |
В результате найдем вектор капиталовложений, естественно в единицах, в которых построены балансовые уравнения МОБ:
|
ΔX |
|---|
|
19,8 |
|
27,2 |
|
87,0 |
|
41,4 |
|
51,4 |
|
Всего фондов |
||||
|---|---|---|---|---|
|
0,080 |
0,012 |
0,013 |
0,001 |
0,008 |
|
0,160 |
0,600 |
0,150 |
0,240 |
0,583 |
|
0,072 |
0,040 |
0,640 |
0,135 |
0,084 |
|
0,012 |
0,001 |
0,013 |
0,168 |
0,008 |
|
0,150 |
0,060 |
0,090 |
0,120 |
0,400 |
|
FΔX |
|---|
|
3,5 |
|
72,4 |
|
68,1 |
|
8,8 |
|
37,9 |
В плановом расчете наоборот: чтобы найти валовые выпуски, надо прибавить эти суммы к вектору потребления и на полученный вектор конечного продукта в целом умножить матрицу коэффициентов полных затрат. Тот же результат можно получить и прямо умножением на вектор потребления матрицы H*.
В нашем примере для этого необходимо рассчитать разность Y-FΔX, т. е.
|
Потребление |
|---|
|
52 |
|
160 |
|
1042 |
|
1038 |
|
3112 |
|
FΔX |
|---|
|
3,5 |
|
72,4 |
|
68,1 |
|
8,8 |
|
37,9 |
|
П=Y-FΔX |
|---|
|
48 |
|
87 |
|
974 |
|
1029 |
|
3074 |
При вычислении разницы матриц Y-FΔX, возможны неточности, связанные с округлением векторов
Пусть производственные мощности допускают получение того валового выпуска, который обеспечил или обеспечит в предстоящий год такие дополнительные вложения вместе с вектором потребления, тогда задача получает решение только для одного изолированного периода, т.е. по существу становится статической. Уже в последующем периоде найденного валового выпуска вместе с его приростом может оказаться недостаточно даже для возмещения выросших затрат.
Подлинно динамическая постановка задачи вообще не допускает рассмотрение приращения (или темпов) для разных отраслей как независимых друг от друга. Могут быть заданы лишь линии изменения фондов потребления Пi, валовые же выпуски вместе с линиями их изменения определятся как результат решения задачи. Данный вывод важен и не случаен. Можно определить конечное потребление Пi, но валовые выпуски Xj можно определить после решения задачи - вычислив матрицу полных затрат – H*=(E-A-B-FK)-1.
Это, значит, что в уравнениях (2) Пi заданы в виде функций времени, а Xi -такие функции времени, которые вместе с их приращениями удовлетворяют всей системе уравнений:
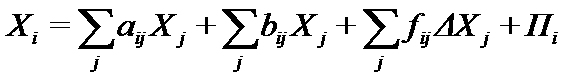
где fijΔXj есть прирост ΔФij фондов j-и отрасли из продукции i-й отрасли.
Мы пришли к системе конечно-разностных уравнений:
где П - вектор заданных функций времени, X - вектор неизвестных функций времени, выражающих валовые выпуски, А, В и F - известные нам из предыдущего матрицы.
Если же рассматривать процесс не по дискретным ступеням времени, а как непрерывный, то П и X превращаются в dX/dt векторы-потоки, а ΔX заменяется вектором производных
Если задать для всех составляющих П один и тот же темп k, то эти составляющие предстанут как
Можно пытаться искать решения для составляющих X, растущих тем же темпом k.
Это значит искать их для:
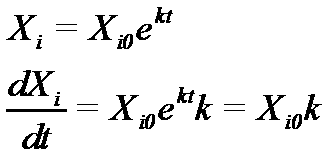
Подставив это в X=(A+B)X+F(dX/dt)+П, после сокращения на ekt получаем
где X0 и П0 - векторы, состоящие из Xi0 и Пi0.
Это приводит к решению
Смысл его состоит в следующем: если заданы начальные значения Пi0 всех Пi и общий для них темп k, то при найденных начальных валовых выпусках Хi0 обеспечивается заданный темп роста при стабильной структуре производства.
Но, разумеется, это отнюдь не единственно возможное решение системы:
В частности, до достижения стабилизации в указанном выше смысле, в составе решения могут быть и слагаемые, содержащие тригонометрические функции, удельный вес которых будет постепенно уменьшаться. О предельно возможном при данных А, В, F общем темпе k речь была выше. Необязательно и изменение Пi по показательным функциям с одинаковым темпом роста.