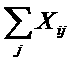Глава 2.3 Статическая модель межотраслевого баланса

АЛГОРИТМ - Статическая модель межотраслевого баланса

Рассмотрим основные допущения, начальные и граничные условия и последовательность, алгоритм расчетов статической модели МОБ.

Основная идея модели МОБ достаточно проста. Данную идею можно представить легко: «чтобы что-то произвести, нужно что-то затратить».

Для того чтобы произвести любой продукт для конечного потребления (конечные товары и услуги), т.е. обеспечить конечный спрос - Y_i, необходимо часть товаров и услуг 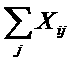затратить в процессе производства данного конечного продукта.

Вспомним, как описываются индексы матрицы X_ij. Для нашего случая i - номер строки - номер некоторого продукта, j - номер столбца - номер предприятий некоторой отрасли, которые производят данный продукт.

Таким образом, чтобы обеспечить валовой выпуск продукции i-х товаров и услуг X_i необходимо часть i-х товаров и услуг, произведенных различными j-ми отраслями 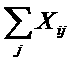затратить на производство i-х конечных Y_i товаров и услуг. Общую модель МОБ можно представить в виде:

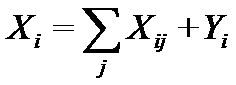
Соответственно, для того чтобы определить конечный продукт, или конечный спрос, или ВВП достаточно провести элементарный перенос переменных:

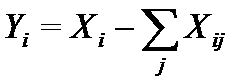
Для расчета коэффициентов прямых затрат для производства продукции j-й отрасли необходимо разделить все внешние материальные затраты различных предприятий i-х отраслей X_ij на объем продаж j-й отрасли X_j.

В результате получаем коэффициенты а_ij прямых затрат i-го продукта на единицу j-го продукта, т.е. на его производство. Данные расчеты можно представить в виде:

a_ij=X_ij/X_j

или в матричном виде еще проще – А.

Подставив это выражение в 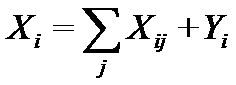, получаем систему уравнений:

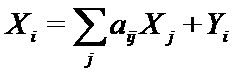
Или в матричной форме:

X=AX+Y

где X и Y - векторы, и А - матрица коэффициентов прямых затрат а_ij.

Вектор X - валовой выпуск - отражает весь объем производственной деятельности, а вектор Y - ее конечный результат или конечный спрос, ВВП. Из X=AX+Y получаем

Y=X-AX=(E-A)X

где E - единичная матрица, на диагонали которой находятся «1», а все другие элементы матрицы «0».

Отметим экономический смысл единичной матрицы – это ничто иное, как производство одной единицы «1» конечной продукции каждой отраслью. Чтобы отразить данный момент «1» размещены на диагонали матрицы, а во всех остальных ячейках записываются «0».

Так как целью производства является производство конечной продукции - Y, то можно поставить вопрос:

Каким должен быть объем производства X и его структура, чтобы обеспечить получение запланированного конечного спроса Y и его структуры.

Решая уравнение Y=X-AX=(E-A)X, получим для X:

X=(E-A)^-1Y

Возможен и обратный вопрос: Каким будет конечный спрос Y и его структура при планируемом объеме производства X и его структуры.

Y=(E-A)Х

Практически получена модель МОБ бесспорно в рамках принятых допущений, начальных и граничных условий.

АЛГОРИТМ - Статическая модель межотраслевого баланса

ЗАМЕЧАНИЕ. Для реализации международной программы сопоставления развития различных стран-членов ООН в системе национальных счетов СНС ООН в рамках МОБ предусмотрена единая классификация основных средств (Ф), и соответственно та же классификация по показателям: амортизации (В), сроку службы (Т), инвестициям (FK).

В рамках этой классификации все предприятия, всех отраслей, всех стран-членов ООН готовят/формируют ежегодную статистическую отчетность.

Понятно, что используя эту отчетность многие вычисления можно осуществлять более просто, исходя из имеющихся статистических таблиц или интернет баз данных.

Так, например, в интернет базах данных США эти массивы информации: основных средств (Ф), и соотвественно по амортизации (В), сроку службы (Т), инвестициям (FK) по основным секторам/отраслям, начиная с 1947г. по настоящий отчетный период, представлены достаточно подробно. Для этого достаточно посетить интернет источник бюро экономического анализа министерства торговли США и скачать базу данных – http://bea.gov/national/FA2004/Details/Index.html. На этом же сайте можно найти множество других показателей, счетов по национальной экономике США — http://bea.gov/national/index.htm, а также уже исходных, обработанных и готовых таблиц МОБ как в ценах потребителей, так и в ценах производителей — http://bea.gov/industry/io_annual.htm. Данные по персоналу (профессии, численность, оплата труда) рекомендуем уточнять на сайте бюро трудовой статистики министерства труда США — http://stats.bls.gov/oes/current/oessrci.htm.

Все интернет базы данных стран-членов ООН отражают все исходные статистические показатели от рабочего места персонала любых организаций:

1. по всем материальным затратам всех отраслей, рынков,
2. по персоналу по отраслям, рынкам, регионам: классификация профессий, численность, профессиональные группы, подразделения/центры ответственности, компенсация, часовая/годовая оплата труда, процентные социальные, пенсионные отчисления,
3. по основным средствам (Ф), амортизации (В), сроку службы (Т), инвестициям (FK) по отраслям, рынкам, регионам,
4. по прибыли по отраслям, рынкам, регионам,
5. по субсидиям/налогам по отраслям, рынкам, регионам,
6. по процентным доходам/расходам по отраслям, рынкам, регионам,
7. по ценам, по доходам, по логистике, и т. д. по отраслям, рынкам, регионам.

Без этих статистических данных невозможно построить МОБ, СНС и, наконец, рассчитать столь любимый либеральными экономистами показатель ВВП. Подчеркнем, статистических данных собираемых исключительно с рабочего места персонала, на всех последующих уровнях они лишь суммируются/интегрируются.

Очевидно, что эти подробные, в т.ч. интегрированные, статистические базы данных необходимы для анализа, планирования, контроля, моделирования в рамках МОБ. Как можно чем-то управлять на уровнях: организаций, отраслей, регионов, министерств, правительства, государства не имея этих данных.

Со времен фараонов любой земледелец хорошо знал, чтобы обеспечить семью хлебом каждый год, необходимо урожай текущего года разделить на несколько частей:

• часть урожая оставить для посева,
• часть урожая сохранить для посева, если ожидается увеличение семьи,
• часть урожая сберечь как страховой запас на случай неурожая,
• и только оставшуюся часть урожая можно будет потреблять семье земледельца в течение года.

В данном примере не рассматривалось разделение труда, т.е. исследовалась модель с одним производимым продуктом - зерном.

Итак, модель землепашца или межотраслевого баланса (МОБ) можно представить в виде:

X_i=∑X_ij+Y_i

где Х_i - всего объем производства конкретной продукции, например хлеба,

∑X_ij – сумма всех затрат по колонке j для производства конечного продукта, например хлеба,

Y_i. – собственно вектор потребления или конечный продукт, например хлеб.

Переведем эту упрощенную модель, известную задолго до времен фараонов и представим ее в экономических терминах, в рамках которых весь общественный продукт, и как следствие модель МОБ можно представить в виде четырех частей:

• фонд возмещения (материальные затраты в производстве или промежуточный спрос);
• фонд расширения производства (производственное накопление или инвестиции);
• страховой фонд;
• фонд потребления (ВВП или конечный спрос).

Понятно, что знание этих величин для анализа состояния и динамики экономики, для планирования и управления недостаточно, нужна их детализация.

Конечно, при этом следует рассматривать не весь общественный продукт в целом, а отдельные его составляющие - конкретные продукты или их группы. Если весь общественный продукт распадается на указанные части, то, вообще говоря, то же можно сказать и о конкретном продукте.

Вернемся опять к нашему примеру. При производстве зерна:

• первая часть его сбора возмещает семена, затраченные при посеве в предыдущем периоде,
• другая часть используется как дополнительный семенной фонд для увеличения его производства в следующем году,
• третья используется в потреблении,
• четвертая оставляется как страховой фонд на случай неблагоприятных метеорологических условий в будущем.

Но если первая часть зерна возмещает семена, затраченные в его же производстве, то множество других продуктов должно возмещать их затраты в ряде отраслей.

Отсюда идея разбивки фонда возмещения (материальные затраты в производстве, промежуточный спрос) не только по образующим его продуктам (или их группам), но в производстве каких других продуктов они были затрачены. В результате получается «шахматная» таблица. В таблице строки это вид, номенклатура затрачиваемых продуктов, а столбцы – перечень тех же продуктов, как их потребителей, в роли которых выступают предприятия различных отраслей.

Такая таблица образует так называемый первый квадрант межотраслевого баланса. Впервые такая таблица была составлена советскими экономистами по данным 1923/24 хозяйственного года. В настоящее время такие межотраслевые балансы составляются во многих странах. Их часто на западе называют балансами «затраты – выпуск» или «input-output».

Пусть производство состоит из n перенумерованных видов, i - номер некоторого продукта. На практике - некоторой группы продуктов. Обозначим весь выпуск этого продукта X_i. Размер потребления (промежуточный спрос) этого i-го продукта в производстве j-го продукта обозначим X_ij. Таким образом, общее количество i-го продукта, вошедшего в фонд возмещения, для производства другого j-го продукта, составляет 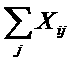, а весь фонд возмещения 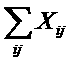(в суммарном стоимостном выражении).

Числа X_ij и заполняют шахматную таблицу, в которой i - номер строки - номер некоторого продукта, j - номер столбца - номер предприятий некоторой отрасли. Эту таблицу можно трактовать и как матрицу (X_ij). Сами же выпуски (объемы продаж предприятий каждой отрасли) образуют вектор, который будем считать столбцом и обозначать X. Таблица X_ij показывает межотраслевые связи производств, отсюда и название – «межотраслевой баланс».

Из таблицы видно, сколько каждого продукта было (будет) использовано (потрачено, потреблено) в производстве каждого другого продукта, как и в производстве его самого, если i=j. В целом первый квадрант показывает промежуточный спрос, который складывается в процессе производства общественного продукта.

Второй квадрант.

Если общий объем производства X_i можно представить в виде суммы промежуточных затрат, спроса - 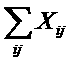, а конечный спрос, потребление в виде Y_i, т.е. 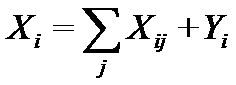, то несложно определить конечный спрос:

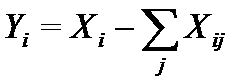
Собственно Y_i образует вектор Y, который называют конечным продуктом, конечным спросом или ВВП.

В развернутом виде в таблице МОБ вектор конечного спроса Y раскладывается в свою очередь на вектора. Т.е. практически вектор Y состоит из векторов:

• Вектор личное потребление - в международной системе национальных счетов (СНС) это термин «Personal consumption expenditure».
• Вектор капиталовложения в СНС это «Gross private fixed investment».
• Вектор изменение в материальных запасах на конец периода в СНС это «Change in business inventories».
• Вектор потребление отраслей непроизводственной сферы, т.е. государственные, социальные, военные расходы. В СНС это термин «Government consumption expenditures and gross investment».
• Вектор экспорта-импорта, можно отобразить как сальдо, или как два вектора – вектор экспорта и вектор импорта. В СНС это термин «Export and Import».

Отметим, что это векторное поле конечного спроса можно также представить еще более детально.

Третий квадрант образует таблица добавленных стоимостей составных частей стоимости продуктов, кроме учтенных в первом квадранте материальных затрат - заработная плата, единый социальный налог, косвенные налоги, НДС, амортизация (если она не включена в материальные затраты), процентные выплаты, прибыль.

В целом МОБ можно описать в виде таблицы из четырех квадрантов:

Или в виде развернутой таблицы МОБ общественного продукта:

Замечание. Сумма элементов строки и колонки параметра «Валовой продукт» равны.

Условно-чистая продукция 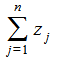в международной системе национальных счетов (СНС) определяется как добавленная стоимость.

Валовой продукт – в СНС определяется как «выпуск» или «output». Практически это объем продаж или выручка.

Рассмотрим, как рассчитываются прямые затраты.

Делением X_ij на X_j получают коэффициенты а_ij прямых затрат i-го продукта на единицу j-го продукта, т.е. на его производство:

а_ij = X_ij/X_j

Таким образом,

X_ij = а_ij*X_j

Подставив это выражение в 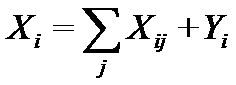, получаем систему уравнений:

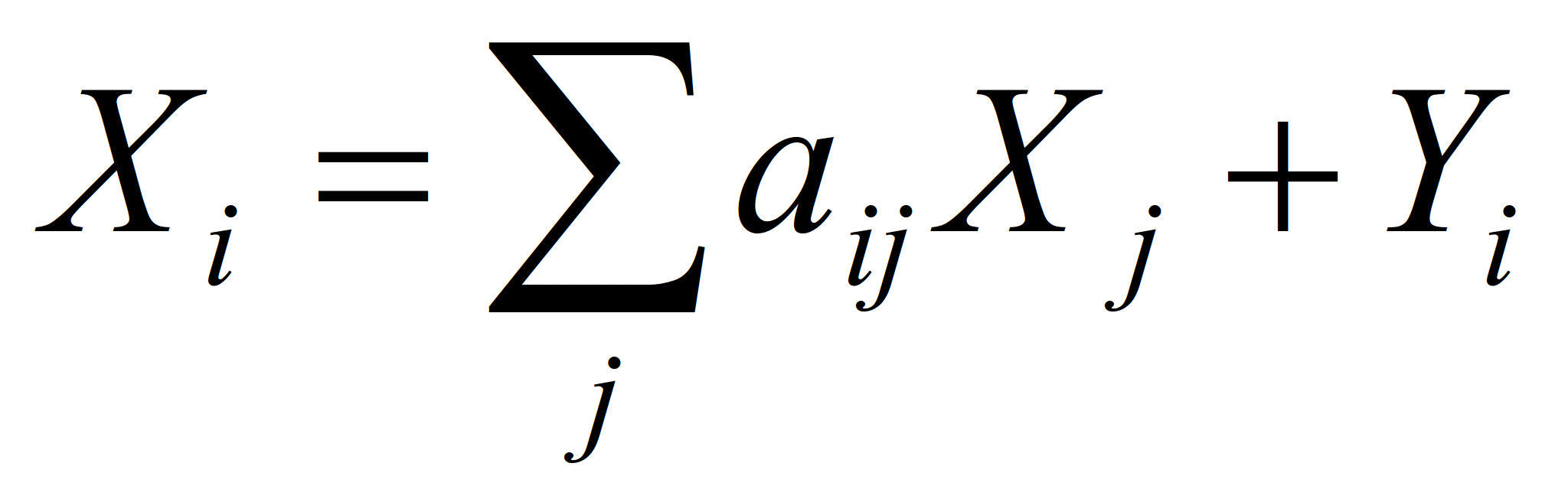
- выпуск i-го продукта состоит из его затрат в производстве других продуктов (включая, если надо, и его самого) и конечного продукта. Отметим, что данное уравнение описывает взаимодействие I и II квадрантов.

Подробнее это уравнение для каждого i-го продукта:

X_i= а_i1X₁ + а_i2X₂ + …+ а_inX_n + Y_i

Зависимость 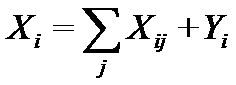можно описать в матричной форме:

X=AX+Y

где X и Y - векторы, и А - матрица коэффициентов прямых затрат а_ij.

Вектор X - валовой выпуск - отражает весь объем производственной деятельности, а вектор Y - ее конечный результат или конечный спрос, ВВП.

Проведем простейшие преобразования X=AX+Y, для этого:

Y=X-AX=(E-A)X

где E - единичная матрица (на диагонали которой «1», а все другие элементы «0»).

Отметим экономический смысл единичной матрицы – это ничто иное, как производство одной единицы «1» конечной продукции каждой отраслью. Чтобы отразить данный момент «1» размещены на диагонали матрицы, а во всех остальных ячейках записываются «0».

Так как целью производства является производство конечной продукции - Y, то можно поставить вопрос:

Каким должен быть объем производства X и его структура, чтобы обеспечить получение запланированного конечного спроса Y и его структуры.

Решая уравнение Y=X-AX=(E-A)X, получим для X:

X=(E-A)^-1Y

Возможет и обратный вопрос:

Каким будет конечный спрос Y и его структура при планируемом объеме производства X и его структуры.

Y=(E-A)Х

Мы пришли к основной математической задаче, решаемой на основе межотраслевого баланса. Равенство X=(E-A)^-1Y показывает, каков должен был быть валовой выпуск X для обеспечения данного конечного продукта Y, как он сложился вследствие имевших место коэффициентов затрат, зафиксированных в матрице А. (E-A)^-1 показывает то же в виде системы относительных величин.

Поясним, почему обратная матрица (E-A)^-1 тем больше, чем больше элементы матрицы А. Это вытекает из азбучного понятия - ведь если из единичной матрицы «1» вычесть матрицу А, а затем разделить «1» на полученное значение – 1/(E-A)=(E-A)^-1. Становится понятно, что чем больше элементы матрицы А, то разница E-A будет меньше, а чем меньше знаменатель, тем больший результат от деления.

Т.е. (E-A)^-1 тем больше, чем больше элементы матрицы А.

Для того, чтобы лучше понять, почему с увеличением матрицы прямых внешних затрат А наблюдается рост обратной матрицы (E-A)^-1, рассмотрим простейший математический пример только без использования матричных вычислений.

Пусть доля внешних затрат в объеме продаж у предприятий первой отрасли (А₁) составляют всего 20%, т.е. А₁=0.20, тогда 1/(1-0.2)=1/0.8=1.25.

Положим, что доля внешних затрат в объеме продаж у предприятий второй отрасли (А₂) выше, чем у предприятий первой отрасли и составляют 50%, т.е. А₂=0.5, тогда 1/(1-0.5)=1/0.5=2.

Допустим доля внешних материальных затрат в объеме продаж у предприятий третьей отрасли (А₃) составляют 80%, т.е. А₃=0.8, тогда 1/(1-0.8)=1/0.2=5.

Экономический смысл (E-A)^-1 можно определить следующим образом, чем больше величины внешних затрат фирмы, элементы матрицы А, тем сложнее технологии, выше уровень разделения труда, тем больше предприятий участвуют в производстве конечного продукта.

В линейной алгебре известно разложение в степенной ряд матриц:

(E-A)^-1=1/(E-A)=E+A+A²+…+A^m+…

При условии, если A^m→0 при m→∞.

Очевидно, что если существует (E-A)^-1 и A^m→0 (при m→∞), то полные материальные затраты, без учета конечной продукции Е составят:

С=(E-A)^-1-Е

Это разложение является принципиальным моментом.

Для математики данный подход достаточно логичен, но в реальной экономике условие A^m→0 при m→∞ выглядит как минимум дико. Любая технология, любое разделение труда при любой технологической формации конечно, но никогда не может устремляться в бесконечность. Мало того, нам важно разделить индивидуально все и каждую отрасль на конечные уровни технологического разделения труда, а они, как и показывают расчеты:

• Каждая отрасль имеет свой индивидуальный уровень разделения труда.

• Количество технологических циклов не только индивидуально, но и конечно.

В этих условиях прямое применение разложения в степенной ряд матриц:

(E-A)^-1=1/(E-A)=E+A+A²+…+A^m+…

Условие A^m→0 при m→∞ экономически бессмысленно и не правильно!!!

Остановимся подробнее на соотношении матриц:

А и (E-A)^-1

В производстве любого продукта тратятся материалы (сырье, энергия, топливо, в том числе и услуги). Но в производстве этих материалов также расходуются материалы, и данный цикл опять многократно повторяется через все промежуточные звенья.

Если просуммировать все такие затраты - не только прямые, но и косвенные, т.е. затраты через все промежуточные звенья, то придем к полным затратам. При расчете их на единицу продукта получим коэффициенты полных затрат одних продуктов в производстве других. Эти полные затраты значимо превышают прямые затраты.

Величина превышения полных затрат над прямыми определяется уровнем, сложностью технологий, используемых при производстве тех или иных товаров и услуг. Из модели межотраслевого баланса вытекает главное – вся модель МОБ основывается исключительно на уровне разделения труда. Модель МОБ определяет труд, а не деньги и прочие вторичные экономические категории.

Коэффициенты полных затрат и определяют размер валового выпуска X, необходимого для обеспечения конечного продукта Y.

Они определяют, сколько надо произвести (промежуточный спрос) i-го продукта (см. по строкам МОБ) для получения одной единицы каждого j-го конечного продукта (см. по столбцам МОБ). Если же считать, что в них учитывается полностью вся производственная программа (объем реализации или продаж предприятий данной отрасли, см. форму 2 публичной бухгалтерской отчетности), выполнение которой приводит к получению единицы j-го продукта, то в нее должно включаться и производство ее самой.

В отличие от этого под полными материальными затратами (матералоемкость - С) понимаются только затраты в собственном смысле слова разных продуктов, которые было необходимо произвести для получения единицы данного продукта, не считая производство ее самой:

С=(E-A)^-1-Е

Среди них может числиться и данный продукт, но только в качестве затраченного средства, как, например, зерно на семена. Будем придерживаться первой трактовки, как это и следует прямо из:

(E-A)^-1

Таким образом, валовой выпуск, обеспечивающий получение этой единицы 1-го продукта, равен вектору, образующему в (E-A)^-1 ее первый столбец. Аналогично валовой выпуск, обеспечивающий получение после возмещения затрат единицы 2-го продукта, образует в (E-A)^-1 ее второй столбец и т. д.

Итак, матрица (E-A)^-1 есть матрица коэффициентов полных затрат. Получение ее на основе коэффициентов прямых затрат А и является важнейшей задачей, решаемой на базе МОБ.

Матрица же коэффициентов полных материальных затрат (материалоемкость), т.е. коэффициентов, определяющих всю производственную программу, обеспечивающую получение единицы каждого продукта без производства ее самой, есть

(E-A)^-1-Е

Знание коэффициентов полных затрат исключительно важно для планирования, а также для анализа динамики кризисных процессов.

Например, при внесении изменения в план в виде увеличения некоторого конечного продукта Y без учета матрицы полных затрат пришлось бы непосредственно подсчитывать, сколько для этого надо дополнительно материалов, затем, сколько надо дополнительно материалов на производство этих материалов, и т.д. - проделать много кругов балансирования производств друг с другом. Знание коэффициентов полных затрат позволяет сразу определить дополнительную производственную программу X для всех отраслей.

Межотраслевой баланс является исключительно ценным средством в планировании.

Для нас это принципиально важно, т.е. предприятие без этих данных не только не в состоянии обеспечить эффективное планирование, анализ и контроль, но и в целом не в состояние эффективно управлять. По разным оценкам внешние факторы предприятия могут составлять до 80%.

Коэффициенты прямых затрат получаются непосредственно из учетных данных каждого производства, т.е. из публичной бухгалтерской отчетности предприятий, организаций, каждый показатель которой расширен и дополнен. Например, численность персонала в публичной отчетности дана одной цифрой. В системе национальных счетов для построения МОБ эта цифра расшифровывается на тысячи показателей: по профессиям, структурным подразделениям, по отработанному времени каждого сотрудника, каждой профессии, его часовой оплате труда, травматизму и т.д.

Если же данный продукт производят несколько предприятий, то средние по ним коэффициенты прямых затрат, охватывающие все производство данного продукта, могут быть получены только на уровне отрасли. Коэффициенты же полных затрат, для получения которых надо решить систему

Y=X-AX=(E-A)X

в целом или вычислить по формуле (E-A)^-1, могут быть рассчитаны только центральным статистическим органом страны:

Y=X-AX=(E-A)X

(E-A)^-1

В ряде случаев это относится и к коэффициентам прямых затрат, если продукт производится на предприятиях, подчиненных разным вышестоящим организациям, как, например, каменный уголь, металлы и т.д., производство которых ведется предприятиями нескольких отраслей.

При обеспечении составления межотраслевого баланса информацией возникает вопрос о разнесении затрат каждого предприятия по отдельным продуктам. Первичные данные для этого имеются, поскольку на них основывается калькуляция себестоимости. Конечно, собирать в центр все калькуляции конкретных продуктов, которых миллионы, более чем трудно. Поэтому приходится концентрировать их на «единицу» агрегированной группы. Но и таких агрегированных групп на предприятии оказывается несколько, причем некоторые из них даже не относятся к той отрасли, к которой принадлежит предприятие. Например, некий автозавод кроме автомобилей производит холодильники, тракторы, прицепы и т.д. В связи с этим возникает необходимость перегруппировки данных о затратах с целью выделения так называемых «чистых» отраслей производства.

При вычислении (E-A)^-1 на основании А для сколько-нибудь значительного числа отраслей при ручном счете оказывается непосильной работой. Только современная вычислительная техника сделала возможным его осуществление для баланса по сотням, тысячам отраслей.

Рассмотрим процесс построения модели МОБ в рамках СНС на примере баланса пяти отраслей (см.табл.1.).

В первую отрасль включаются предприятия сырьевых отраслей в системе национальных счетов это предприятия сельскохозяйственной отрасли – «Agricultural» и предприятия горно-добывающей и нефтегазовых отраслей – «Mining».

Во вторую отрасль включим предприятия строительной отрасли, в рамках системы национальных счетов обозначим их – «Construction».

В третью отрасль включим предприятия отрасли машиностроения, в рамках системы национальных счетов обозначим их – «Manufacturing».

В четвертую отрасль включим банки, страховые, фондовые, трастовые компании и компании по продаже недвижимости, в рамках системы национальных счетов обозначим их – «F.I.R.E».

В пятую отрасль, в рамках системы национальных счетов будем агрегировать следующие отрасли:

• Предприятия транспортной отрасли «Transportation, communication and utilities».
• Предприятия отрасли оптовой и розничной торговли «Trade».
• Предприятия отрасли сервиса и услуг «Services».
• Предприятия других отраслей, не вошедших в ранее перечисленные отрасли, их обозначим в рамках СНС как «Other».

Напомним, по строкам даны продукты, которые потребляются отраслями промышленности для производства конечного продукта или ВВП, по колонкам даны отрасли народного хозяйства.

Рассмотрим алгоритм расчета МОБ.

На первом шаге определим долю всех элементов прямых затрат в общем объеме производства, для этого проведем деление по колонкам X_ij на X_j, в результате получаем матрицу коэффициентов прямых затрат:

Уточним — деление проводим по колонкам:

X₁₁/X₁ = 82/395=0.21; X₂₁/X₁ = 6/395=0.02; X₃₁/X₁ = 51/395=0.13; и т.д.

X₁₂/X₂ = 9/680=0.01; X₂₂/X₂ = 1/680=0.001; X₃₂/X₂ = 203/680=0,3; и т.д.

Остальные расчеты аналогичны – деление производится по вертикали. Выпуск X_j выделен жирным и находится на горизонтальной строке внизу.

Единичную матрицу традиционно представляют в следующем виде:

На втором шаге определим величину добавленной стоимости, конечного производства или конечного спроса, для чего вычтем из каждого элемента единичной матрицы «Е» значения элементов матрицы прямых затрат А:

На третьем последнем шаге рассчитаем величину матрицы коэффициентов полных затрат

H=(E-A)^-1:

ЗАМЕЧАНИЯ ДЛЯ МОДЕЛЕЙ МОБ США ИЛИ МОДЕЛЕЙ ЛЕОНТЬЕВА (input-output)

В таблице полных затрат, диагональные ячейки почти всегда больше чем единица.

Т.е. чтобы получить один доллар конечного спроса необходимо произвести больше чем один доллар объема продаж, что и требуется произвести предприятиям каждой отрасли.

Недиагональные ячейки всегда меньше единицы.

Диагональ может быть меньше чем единица, если большая часть товарного производства на выходе - это вторичные продукты. Предполагается, что все отрасли выпускают только 1 вид продукции, т.е. первичные продукты. Иногда, кроме основных - первичных продуктов предприятия той или иной отрасли выпускают вторичные продукты.

Если вторичных продуктов больше чем первичных продуктов, то Диагональ будет меньше чем единица.

Данный вид учета по первичным и вторичным продуктам легко проверить. В МОБ США в отличии от МОБ СССР валовой выпуск по строкам (товарам) и по колонкам (отраслям) никогда не равны. Ниже дан учет по МОБ СССР.

В СССР отчетность предприятий ПРЕДУСМАТРИВАЛА вести учет!!! по всем видам продукции!!!
В МОБ важен вид продукции в рамках системного принципа «производить подобную продукцию, подобными технологиями». В СССР Вид Продукции, ее Однородность определяет Отрасль!!!
В США нужно послать 10-к официальных запросов :) на фирмы, чтобы получить отчет по всем видам продукции :) США методику МОБ СССР передрали, а отчетность не поменяли :) ПЕРЕДЕРАТЬ ТОЖЕ НУЖНО УМЕТЬ:)

Величина коэффициента полных затрат - индикатор силы отношений между конечным спросом и выходом/output (объемом продаж). Чем большее коэффициент, тем сильнее отношение.

Прямое преобразование (сумма по строке) - сила связи отрасли промышленности к изменениям конечного спроса. Чем большее коэффициент, тем сильнее отношение.

Обратное преобразование (сумма по колонке) проявляют относительную силу конечного спроса и выходом/output (объемом продаж). Чем большее коэффициент, тем сильнее отношение.

В самом общем и простом виде этим и исчерпывается суть модели межотраслевого баланса и главной решаемой на ее основе задачи. В изложенном виде она называется статической, так как замыкается рамками одного периода (как правило, года) и, таким образом, в ней отсутствует всякая динамика или обеспечение этой динамики в будущем: конечный продукт пока никак не расчленен на потребление и накопление или инвестиции.

В теоретическом изложении можно считать, что каждому конкретному продукту выделяется отдельная «позиция» в балансе - строка и столбец. Естественно при этом измерять его можно в натуральном выражении или в соответствующих натуральных единицах, например - уголь в тоннах, электроэнергия в тысячах киловатт-часов, автомобили в штуках, хлеб в количестве батонов и т.д. Но можно продукты измерять и в ценах - в рублях по их соответствующей оценке. Если X_i было выражено в натуральных единицах, то для перехода к измерению в ценах надо X_i умножить на цену i-го продукта р_i.

То же относится и к части его, затраченной в производстве j-го продукта. А для перехода к такому измерению надо X_j также умножить на его цену р_j. В результате получим коэффициент прямых затрат в рублях на рубль:

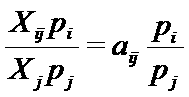
Для перехода от коэффициента затрат в натуральном измерении к коэффициенту затрат в ценах надо умножить его на цену затрачиваемого продукта и поделить на цену того продукта, затраты на который исчисляются.

Получатся затраты в рублях на 1 руб. продукции. Возможно построение и смешанной матрицы коэффициентов, которая получится при измерении одних продуктов в натуральном выражении, а других в ценах. Например, умножив затраты электроэнергии на 1 т угля на цену 1 кВт-ч электроэнергии, мы получим затраты на 1 т угля в рублях, которые надо заплатить за электроэнергию (что прямо и входит как слагаемое в калькуляцию себестоимости угля). С другой стороны, при таком измерении получим затрату угля в тоннах на получение электроэнергии стоимостью в 1 руб.

Переход к измерению в ценах неизбежен при агрегировании продуктов в группы. Даже если формально при этом можно сохранить натуральную единицу измерения, измерение в ценах оказывается, как правило, лучшим. Продукцию обувной фабрики можно измерять числом пар обуви, на ней изготовленной. Но одно дело простенькие детские ботиночки, другое - модельные сапоги, третье - дамские модельные туфли. Цены как-то учитывают эти различия (в том числе и затраты кожи и других материалов, поскольку в установлении цен так или иначе учитывается себестоимость), и потому оказываются лучшей мерой, чем абстрактная пара обуви.

При практическом же построении баланса в натуральном выражении и выделении в нем ряда конкретных продуктов неизбежно приходится их перечень замыкать разными группами «прочих продуктов» - прочие продукты основной химической промышленности, прочие продукты горнодобывающей и т. д. Тогда и возникает смешанная система коэффициентов затрат, когда для конкретных продуктов сохраняется измерение в натуральном выражении, а для групп «прочих» неизбежно измерение в ценах.

Для стоимостного баланса возникает вопрос, в каких именно ценах измерять продукцию? Это могут быть текущие фактические цены или некоторые сопоставимые (базисные). Для отдельного баланса этот вопрос не столь существен. Но для ряда таких балансов или для рассмотрения баланса в связи с другими показателями статистики он приобретает большое значение. Межотраслевой баланс имеет также разные аспекты.

Технологический аспект означает, что в центре внимания - конкретное обеспечение производств материалами. Наилучший вариант для него - натуральное измерение, а цены в этом случае должны как можно ближе отражать натуру, физический объем продукции и затрат на нее. Очевидно, это сопоставимые цены, используемые вообще для измерения физического объема продукции и т. п. Важность этого аспекта так велика, что всю матрицу А нередко называют матрицей технологических коэффициентов.

Возможен и другой аспект, связанный с экономическими расчетами, калькуляцией себестоимости, финансовыми отношениями и т. п. Для него приобретает ценность измерение элементов баланса в ценах, притом фактически действующих. Учитывая важность того и другого аспекта, межотраслевой баланс создают в двух вариантах: по фактически действовавшим ценам и по сопоставимым, по которым в статистике исчислялись другие показатели по народному хозяйству.

Цены могут быть сами по себе разными: оптовые и розничные, локо-место производства и франко-место потребления и т.д. Вопрос о выборе цен решается с учетом взаимосвязи частей баланса, выделения в нем отраслей. Для связи с калькуляцией себестоимости (а это в большой мере обусловливает и преодоление трудностей в получении исходной информации) естественно считать затраты в ценах потребления. Но в таком случае и валовой выпуск должен учитываться в таких же ценах. Следовательно, в балансе должны быть выделены строки затрат, дополнение которыми учтенных в ценах потребления материальных затрат приводит к ценам, по которым данную продукцию получит ее потребитель. Но эти дополнения уже выходят за рамки матрицы материальных затрат А.