Производственно-мотивационная концепция, модель Самариной

К основным недостаткам исследований мотивационных концепций различных экономических школ авторы относят то, что ни одна из школ не смогла перейти от интуитивного, дескриптивного, описательного уровня к четкому эконометрическому построению производственно-мотивационных моделей, функций и затем к практике, которая могла бы или их опровергнуть или доказать.

Рассмотрим теоретическое построение производственно-мотивационной модели, функции, а также эволюцию рассуждений авторов.

Многие исследователи на современном этапе развития мировой экономики признают доминирующую роль внешней среды на деятельность предприятий и классифицируют их по признаку зависимости от масштабности влияния. Они выделяют факторы: государственного уровня; регионального, отраслевого уровня; уровня предприятия (организации), подразделений организации и собственно рабочих мест персонала.

Расчеты показывают, что не менее важную роль играют технологические особенности отрасли и трудовая мотивация персонала предприятия, ее внутренние и внешние факторы, которые формируются и должны регулироваться федеральными, региональными властями и руководством предприятий. Это происходит через рычаги политики доходов и заработной платы, на базе которой должна формироваться монетарно-фискальная политика, но не наоборот. Авторы предлагают существенно расширить классическую производственную функцию и перенести акцент на факторы внешней среды и трудовой мотивации персонала и рассматривать ее в контексте производственно-мотивационной функции Самариной. Более подробно о ее эволюции читатель может ознакомиться в предыдущих книгах авторов.

Производственно-мотивационная функция в понимании авторов это сложная, динамическая, вероятностная, существенно нелинейная многофакторная система, которая формирует начальные и граничные условия всей системы хозяйствующего субъекта. Построение таких моделей возможно только с помощью специального эконометрического программного обеспечения (ПО) класса "Инвест". Оно должно решать не только линейные, и квазилинейные, но главное нелинейные многофакторные уравнения. Каждый из факторов, включенных в модель, оценивается на первом этапе экономистом-экспертом, но окончательное решение по выбору значимых факторов принимается после эконометрического анализа с помощью ПО "Инвест". Если мнение эксперта и результаты расчетов совпадают, то исследуемые факторы включаются в модель, в противном случае они отбрасываются. Таким образом, все факторы в модели подвергаются оценке на значимость, как экономическую, так и статистическую. В деловой игре (ДИ) "Инвест", разработанной авторами, при анализе деятельности предприятий любой отрасли используется более 5000 факторов. В частности, более ста факторов отражают структуру и динамику обновления основных фондов. Численность персонала, его структура, динамика выплат, дифференциация в оплате труда изучается по отрасли в целом, по регионам, в том числе как внутри специальностей, так и между ними. В целом авторы рассматривают данные по свыше 770 сквозным специальностям, по 1170 отраслям и подотраслям, по всем регионам, а также по всем городам с населением свыше 100 тысяч человек. На уровне предприятия ДИ "Инвест" использует данные стандартной публичной отчетности в рамках программ раскрытия информации.

Выше перечисленные статистические данные являются исходными для построения динамических ноосферно-синергетических производственно-мотивационных нейронных моделей.

Для доступности будем использовать упрощенную трактовку концепции авторов, предложенную Е.Егоровой.

Сформируем основные положения работы, начальные и граничные условия, которые необходимы для дальнейших исследований.

Вначале рассмотрим векторное пространство динамической ноосферно-синергетической производственно-мотивационной концепции и нейронной модели. Как отмечают авторы, для сохранения целостности экономических исследований и построения корректных моделей необходимо осуществить их погружение в данное векторное пространство любого экономического явления, и только после этого можно объективно его исследовать. Данные требования авторов концепции логичны, т.к. они вытекают из центральной процедуры системного анализа, основой которой является построение эконометрических моделей, отображающих многообразие факторов и взаимосвязи реальной ситуации (экономики), которые могут проявиться в процессе осуществления решения. В нашем случае это исследование внутренней и внешней среды предприятий любой отрасли.

В данном случае попытаемся оценить модель любого хозяйствующего объекта – организацию, предприятие, отрасль как сложную систему в векторном пространстве концепции авторов. Учитывая, что выбранную концепцию нельзя представить в виде графического образа, впрочем, как и отобразить процесс погружения в виде графиков в данное векторное пространство модели предприятия, отрасли, поэтому представим данный процесс в виде аналитической зависимости. Обозначим вектор оценки эффективности модели предприятия той или иной отрасли (ПО) как YПО.

Далее рассмотрим насколько идеально можно представить предприятие, отрасль по отношению в вектору динамики – данное отображение обозначим как вектор Х1. Далее по тексту векторные функционалы будем воспроизводить выделенным текстом. Отображение модели хозяйствующего объекта на векторе ноосферы обозначим как Х2. Понятно, что ноосфера (Х2) в свою очередь это интегральное описание взаимодействия технологической сферы (Z1), социальной сферы (Z2) и биосферы (Z3), поэтому функционал ноосферы можно представить как Х2=Ф(Z1, Z2, Z3). Очевидный интерес представляет также вопрос возможно ли, предполагает ли рассмотрение международной отчетности, в том числе ее исходных данных, по отношению к синергетическому вектору (Х3), а также к производственному (Х4). И, наконец, позволяет ли международная отчетность раскрыть человеческий капитал в рамках мотивационного (трудового) вектора (Х5). Представим данное 5-ти мерное пространство отображения вектора оценки эффективности модели хозяйствующего объекта в виде аналитической зависимости:

YПО=F(X1, X2, X3, X4, X5) = F(X1, Ф(Z1, Z2, Z3), X3, X4, X5)

Приступим к упрощенному дескриптивному анализу. Рассмотрим насколько совершенно систему хозяйствующего объекта можно представить по отношению в вектору динамики Х1. Для того чтобы можно было наблюдать динамику развития (подчеркнем данный момент), стандарты международной отчетности рекомендуют сравнивать отчетный период и/или с предыдущим отчетным периодом и/или с базовым периодом. Очевидно, что данный подход как минимум не корректен не только со стороны динамической экономики, но даже со стороны здравого смысла. Представление данных в таком объеме не дает возможности проводить динамический анализ, как следствие невозможно определить сезонные, товарные, ценовые, кредитные, инвестиционные, денежные, дебиторские, кредиторские и прочие циклы. Нельзя говорить о столь существенных для экономического анализа фазовых сдвигах, которые могут возникать как между факторами внутренней среды исследуемого хозяйствующего субъекта, так и их амплитудно-временном взаимодействии с многообразием факторов внешней среды. Например, это может быть связано с технологическими особенностями различных производств (на этапах разработки, внедрения, выпуска, в том числе временные затраты на подготовку, адаптацию персонала) и др.

Конечно, что при таком ограниченном восприятии динамики вопрос можно ли, предполагает ли рассмотрение модели хозяйствующего объекта, в том числе ее исходных данных, по отношению к синергетическому вектору (Х3) как минимум лишен смысла. Даже в рамках здравого смысла понятно, что в двух временных отсчетах трудно обнаружить какие-либо ветвления, не говоря о сдвигах, бифуркациях экономических фазовых пространств. Приходится полностью согласиться с основателем синергетики или теории хаоса нобелевским лауреатом И. Пригожиным, который писал, что любые экономические исследования, анализ синергетических мультипликативных бифуркаций (ветвлений) в ограниченном временном пространстве наивны, так как не возможны.

Как следует из материалов конференций ООН, регулярно проходящих в рамках программы ноосферного устойчивого развития, утвержденной руководителями 146 стран мира в 1992 в Рио-де-Жанейро, указом Президента РФ № 440 от 1996 г., какие-либо попытки исследований отобразить интегрированный ноосферный фактор Х2=Ф(Z1,Z2,Z3) при оценке эффективности хозяйствующего объекта не предпринимались. Мало того, как отмечает Е.Рюмина, даже более простой экологический факторный балансовый анализ с трудом пробивает себе дорогу. Рассмотрим для примера порочность принципа Киотского протокола, опирающегося на модель "пузыря". Некорректность данной модели, по мнению авторов, концепции заключается в следующем. Страны с высоким уровнем развития будут переносить (США, ипотечный кризис, вывод машиностроения в третьи страны, основной доход США в основном за счет финансовых спекуляций) и уже настойчиво переводят все свои грязные производства в страны с низким социально-экономическим уровнем развития, такие как Россия и др. страны третьего мира, превращая их в экологические свалки. Т.е. страны с высоким уровнем развития не решают проблемы по переходу на другой более высокий эколого-технологический чистый уровень развития, стремятся разместить эти "грязные" технологии на территорию слаборазвитой страны. В результате третьеразрядные страны - с высоким уровнем социальной напряженности и катастрофически низким уровнем доходов 95% населения облагаются богатыми странами дополнительным экологическим налогом, еще более увеличивая социальную напряженность, обнищание, межгосударственную дифференциацию, увеличивая темпы глобального потепления, терроризм и прочее. По нашему мнению, необходимо брать налог не с того, кто работает на грязных технологиях, а с тех, кто потребляет продукцию, производимую с помощью грязных технологий. Т.е. не с работников этих предприятий и не с народа стран экологических свалок, а с тех стран и тех собственников этих предприятий, которые потребляют эту продукцию и получают сверхдоходы с экологических свалок.

Дескриптивно проанализируем следующую проблему - позволяет ли международная отчетность раскрыть человеческий капитал в рамках трудового мотивационного вектора (Х5) для оценки хозяйствующего объекта.

Для этого необходимо обратиться к времени создания балансовой модели. К сожалению, несмотря на активные попытки средневекового философа схоласта Фомы Аквинского, он так и не смог доказать обществу опасность непонимания роли божественного создания – человека, а также чрезмерного возвеличивания роли процентов и финансовых спекуляций. Потребовались века, чтобы была осознана роль и место человеческого капитала в экономической системе. Становится понятно, почему исторически современные мировоззренческие проблемы международной отчетности, ее рудименты были заложены Лукой Пачоли (Luka Pacholi) в балансовой модели.

Эти мировоззренческие рудименты, присутствующие в международной отчетности, по отношению к мотивационному вектору (Х5) долгое время было трудно доказать. Европейская культура, экономическая мысль требовала экономических расчетов, а не принятия на веру базовых аксиом Торы, Библии и Корана, не говоря уже о философских трактатах Фомы Аквинского. Эта возможность впервые была предоставлена (доказана) в работах экономистов В.Дмитриева, П.Сорокина, В.Леонтьева, С.Кузнеца. Рассмотрим производственную функцию Кобба-Дугласа. Логика ее очевидна и ясна, для того, чтобы что-то произвести (обозначим как Q) необходим капитал (K) и труд (L). Долгое время было не понятно одно, кто же из исходных факторов весомей – труд или капитал. В результате проведенных исследований предприятий обрабатывающих отраслей США в начале прошлого века была получена аналитическая зависимость вида:

Q=f(K, L)=1,01K^0,25L^0,75

Следует обратить внимание, что как видно из модели финансовая составляющая является вторичной (т.к. данные факторы оценивались для простоты не в натуральном, а в денежном выражении) по отношению к фактору технологий или капиталу и фактору человеческого капитала. Понятно, что, будучи вторичной, она не в состоянии содержательно отображать базовые категории, особенно если учесть, как будет показано далее, что финансовое интегральное представление пытается в сжатой, скудной форме описать многообразие факторов, процессов капитала и труда. Это вытекает даже из здравого смысла – современные модели с помощью 50…100 факторов в состоянии ограниченно описать только прямые, но не латентные модели труда и капитала, состоящие как минимум из 1000…5000 факторов.

Как видно из полученной зависимости, роль человеческого капитала (0,75) в три раза более весома, чем капитал (0,25), но это лишь малая часть роли труда. Разумеется, что оплата труда напрямую определяет совокупный спрос. В результате труд, оплата труда, а не капитал и тем более не финансы, в конечном счете, формируют объемы продаж. Для того чтобы понять реальную роль, вес труда, человеческого капитала, мотивации по отношению к капиталу обратимся к книге Г.Форда "Моя жизнь, мои достижения", который независимо от В.Дмитриева в 1921 г. задолго до работ, П.Сорокина, В.Леонтьева, С.Кузнеца на практике пришел к удивительному выводу. Своих успехов, по мнению Г.Форда, он достиг не из-за широкого внедрения конвейерной технологии, всеобщей механизации труда, при которой "…никто из наших людей не переутомляется на работе", а реализации его главной цели "…уделять максимум внимания заработной плате, иначе говоря, сообщать максимальную покупательную способность". По его мнению:

"…Решение вопроса о заработной плате устраняет девять десятых проблем, а техника разрешает остальные", но не наоборот: "…Предприятие, которое скверно платит, всегда неустойчиво".

Отметим, что роль финансов в виду их незначительности и вторичности для реальной, а не спекулятивно-виртуальной экономики он вообще не рассматривал.

Им впервые были заложены практические основы теории трудовой мотивации, человеческого капитала, межотраслевого баланса, которые в дальнейшем развили Питирим Сорокин, А. Маслоу, нобелевские лауреаты В.Леонтьев, Т.Шульц и Г.Беккер. Г.Форд пишет, что когда

"…мы в состоянии давать высокую оплату" персоналу на своих предприятиях, то "…этим выбрасывается много денег, которые содействуют обогащению лавочников, торговых посредников, фабрикантов и рабочих других отраслей, а их благосостояние окажет влияние и на наш сбыт. Высокое повсеместное вознаграждение равносильно росту всеобщего благосостояния".

Уже тогда не зная идеи межотраслевых балансов и существования не только прямых затрат, которые отражены в производственной функции, но и косвенно-латентных связей, затрат, которые реально существуют, но они не видимы, он определил на уровне экспертной оценки, что труд весит 90%, а капитал всего 10%.

Анализ международной отчетности по отношениюк мотивационному вектору (Х5)показал, что в ней не учитывается человеческий капитал. Он по весу в объеме продаж составляет 75%-90% по отношению к основным фондам, процентным ставкам, амортизации, прибыли или по отношению к производственному вектору (Х4). В тоже время в международной отчетности данный интегрированный показатель представлен зеркально наоборот, т.е. количественно факторы финансовой отчетности как минимум в 100 раз превосходят количество факторов труда и капитала. Отметим, что в свою очередь показатели капитала также нарушают объективную экономику, т.к. они количественно также многократно превосходят показатели человеческого капитала. В результате невозможно объективно исследовать экономические процессы и хозяйствующие субъекты, т.к. для экономиста в процессе анализа более 90% факторов латентны (скрыты). Последствия такого поверхностного, наивного анализа очевидны.

Подведем итоги, и если потребуется, расширим и дополним дескриптивный анализ. Для начала рассмотрим существенные отличия классической модели международной отчетности IAS и/или GAAP от предлагаемой в работе модели, способной отвечать требованиям и вызовам современной экономики. Для наглядности обе модели представлены на рис. 1.34. и 1.35. на плоскости.

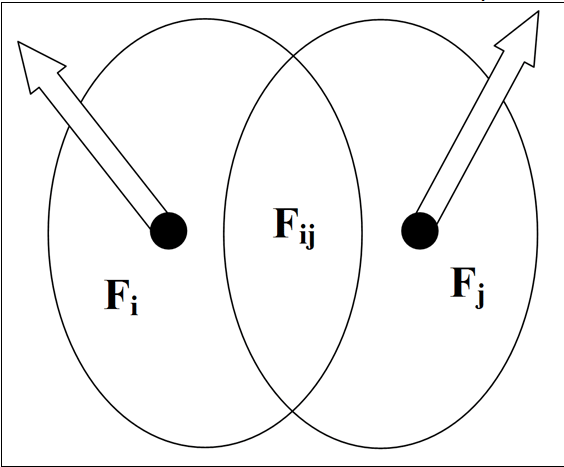
Как видно из рис. 1.34., факторы Fi описывают классическую модель международной отчетности IAS и/или GAAP.

Риc. 1.34. Описание классической модели международной отчетности IAS и/или GAAP

Индекс i определяет конечное счетное множество факторов. В рамках стандарта их около 50-100, т.е. i=1…50…100. Как на интуитивном уровне, так и в рамках теории множеств понятно, что данное ограниченное множество факторов неизбежно формирует пересекающееся множество Fij большой площади. Причина объективна - каждый из факторов имеет высокий уровень интеграции, как следствие при описании модели международной отчетности IAS и/или GAAP для оценки эффективности исследуемой организации формируется высокий уровень неопределенности, далекий от объективных оценок, позволяющий давать только поверхностные оценки в рамках динамической ноосферно-синергетической производственно-мотивационной концепции.

Практически можно утверждать, что экономические службы организаций не анализируют в полном объеме даже прямые связи и затраты, не говоря о косвенно-латентных связях. Как можно в этих условиях говорить об эффективном управлении.

В тоже время, как следует из рис. 1.35. факторы Zk, описывающие предлагаемую в работе модель, тщательно детализируют исходное множество Fi классической модели международной отчетности IAS и/или GAAP.

Рис. 1.35. Описание предлагаемой в работе модели

Индекс k, также как индекс i определяет конечное счетное множество факторов. Только в отличие от классической модели, благодаря предлагаемой в работе детализации индекс k многократно больше индекса i, т.е. k>>i. В рамках предлагаемой модели количество факторов не менее 1000, т.е. k=1…1000. В результате область неопределенности предлагаемой в работе модели Zkl многократно сжимается по сравнению с пересекающимся множеством Fij. В результате при оценке эффективности исследуемой организации нивелируется высокий уровень неопределенности. Понятно, что в этих условиях в предлагаемой в работе модели формируется максимально объективная картина оценок эффективности, коридоров управляемости и рисков исследуемого объекта по сравнению с классической моделью международной отчетности IAS и/или GAAP.

Рассмотрим более существенные моменты недостатков классической модели международной отчетности IAS и/или GAAP по сравнению с предлагаемой в работе моделью. Классические модели в результате высокого уровня интеграции исследуемых факторов опасны не столько высоким уровнем неопределенности, далеким от объективных оценок, сколько тем, что данная отчетность не в состоянии высветить динамические, мультипликативные, синергетические, нелинейные эффекты реальной экономики. Этот экономический эффект, феномен мультипликации и/или синергетической бифуркации, действующий в любой экономике, можно представить, объяснить на интуитивно понятном примере.

Ясно, что если растет совокупный спрос на продукцию некой i-й отрасли, то предприятия этой отрасли для обеспечения данного роста увеличивают закупки (спрос) товаров и услуг у других j-х отраслей, в том числе у предприятий своей i-й отрасли. В свою очередь предприятия этих j-х отраслей увеличивают закупки (спрос) продукции в k-х отраслях. Далее этот процесс циклично продолжается в результате рост спроса на конечную продукцию (товар или услугу) в зависимости от уровня разделения труда, технологической сложности продукции мультипликативно запускает, размножает затраты. Эта потребность в промежуточных товарах и услугах практически всех предприятий различных отраслей инициирует мультипликацию, размножение первичного спроса на конкретный товар i-й отрасли на рост экономики страны в целом. В тоже время существующая классическая модель международной отчетности IAS и/или GAAP предоставляет возможность исследовать только видимые, счетные прямые затраты и в тоже время исключает какую-либо возможность исследовать всю цепь косвенно-латентных затрат во всех предприятиях j-х отраслей не говоря уже о том, что их можно каким-либо способом проследить. Очевидно, что данная проблема это лишь вершина айсберга.

Можно утверждать, что динамический анализ структуры прямых затрат должен выявить высокий уровень временной нелинейности этого вида затрат. В довершение этой скрытой особенности видимых прямых затрат она еще более усугубляется значительной нелинейностью латентно-косвенных затрат, которая усложняется синергетической бифуркацией фазовых временных смещений. Концепция авторов утверждает, что различный уровень технологий для каждого вида товара или услуги, производимых предприятиями соответствующей отрасли, порождает эффект мультипликации и в конечном счете вызывает индивидуальные фазовые сдвиги. Еще раз подчеркнем, каждому товару, услуге соответствуют свои индивидуальные временные, фазовые, амплитудные смещения прямых затрат по отношению к латентно-косвенным затратам.

Все было бы просто для экономического анализа и управления в целом, если бы прямые затраты и соответствующие им латентно-косвенные затраты развивались синхронно (см. рис. 1.36.).

Рис. 1.36. Стандартное представление структуры затрат в классической международной отчетности

В этом случае даже их временная нелинейность в каждой отрасли была бы терпима, т.к. не вызывала бы значительных смещений (ошибок в расчетах и оценках), конечно, в упрощенном представлении.

В реальной же экономике данная зависимость может принимать более чем неординарные состояния (см. рис. 1.37.) по сравнению с синхронным вариантом (см. рис. 1.36.) или отражать промежуточные состояния.

Рис. 1.37. Альтернативный вариант представления структуры затрат в рамках базовой концепции принятой в работе

Авторы концепции утверждают, что для каждой отрасли должны наблюдаться выраженные индивидуальные фазовые синергетические смещения в прямых и косвенно-латентных связях. Косвенным подтверждением важности прямых и косвенно-латентных затрат является различная оценка труда и капитала со стороны Г.Форда (труд -90%, капитал – 10%) и модели Кобба-Дугласа (труд -75%, капитал – 25%). Очевидно, они имеют труднообъяснимый (на первый взгляд) значительный разброс. В тоже время если обратиться к первоисточникам их дескриптивных оценок и эконометрических расчетов, то можно обнаружить, что авторы использовали не столько различный статистический материал, сколько с различной степенью глубины учитывали влияние прямых и косвенно-латентных затрат на исследуемые экономические объекты. Г.Форд в своих оценках более точен по сравнению с авторами модели Кобба-Дугласа. Данная гипотеза на дескриптивном уровне понятна. Г.Форд не просто создал автомобильную компанию, простых автомобильных компаний в США было немало. Он создал всю социально-экономическую инженерно-информационную инфраструктуру от компаний, добывающих уголь, железную руду, металлургических заводов, железнодорожных компаний и так далее до собственно автомобильных конвейерных заводов. Для того чтобы обеспечить своих рабочих, служащих их семьи едой были созданы высоко механизированные фермерские хозяйства.

Для обеспечения всей промышленной инфраструктуры, в том числе жилья и ЖКХ были созданы строительно-монтажные управления. Г.Форд также содержал службы шерифов (полиция штатов), больницы, школы и другую социальную инфраструктуру. Для того чтобы избавиться от непрофессиональной опеки неэффективной финансовой системы США – им была создана своя банковская, фондовая, страховая системы, инвесторами которой был как он сам, так и персонал всех его компаний. Практически он построил государство в государстве и благодаря специально созданному статистическому бюро вел полный контроль, анализ и планирование не только прямых затрат, но и почти всех косвенно-латентных затрат.

Понятно, почему его модель более близка к реальной экономике, чем модель Кобба-Дугласа, которая учитывает в основном только прямые затраты. Как следствие роль труда по отношению к капиталу была занижена. Практически можно утверждать, что сегодняшняя международная система финансовой отчетности находится на эмбриональном уровне даже по сравнению с системой статистического учета Г.Форда.

Одной из важнейших задач управления экономикой является измерение количества труда, содержащегося в продуктах.

Эта задача стала особенно актуальной в связи с проблемой обеспечения производства трудовыми ресурсами. Прежде всего, оно необходимо для распределения фонда рабочего времени, которым располагает общество, или, иными словами, трудовых ресурсов.

Содержащийся в товарах труд, в конечном счете, является основой и для их оценки. И как следствие определение сбалансированных цен и оплаты труда. Отсутствия данного понимания и гармонии будет приводить к росту или деградации экономики и к очередным финансовым кризисам и неизбежно будет порождать пресловутые кризисы перепроизводства.

Первичным источником информации о труде, содержащемся в товаре, является его учет на производстве. Однако непосредственно этот учет дает информацию лишь о труде, затраченном на данной стадии производства продукта, труд же в затраченных на этой стадии средствах производства должен быть учтен еще до нее. Цепь таких взаимосвязей бесконечна.

В производстве любого продукта тратятся материалы (сырье, энергия, топливо, в том числе и услуги). Но в производстве этих материалов также тратятся материалы, и данный цикл опять многократно повторяется через все промежуточные звенья.

Если просуммировать все такие затраты - не только прямые, но и косвенные, т.е. затраты через все промежуточные звенья, мы придем к полным затратам. И если рассчитаем их на единицу продукта, о котором идет речь, то получим коэффициенты полных затрат одних продуктов в производстве других. Эти коэффициенты значительно превышают прямые затраты. Отсюда возникает сложная математическая задача исчисления полного труда в продуктах, тесно связанная с моделью межотраслевого баланса. Т.е. необходимо определить, сколько полного труда затрачено при производстве конечных продуктов. Эта связь, в частности, получила отражение и в межотраслевом балансе труда, составленном советской статистикой на базе межотраслевого баланса продукции. Суть его состоит в том, что на основании имеющихся учетных данных на каждом производстве могут быть определены удельные затраты труда на единицу его продукции. Удельные затраты труда (L) равны общей численности персонала в каждой отрасли, деленной на объем реализации этой отрасли.

Труд мог быть учтен и в других единицах - числе фактически отработанных человеко-дней, еще точнее - человеко-часов, с теми или иными коэффициентами его качества (с редукцией сложного труда к простому), в рублях заработной платы и т. д.

Во всех случаях вслед за тем возникает задача определения всего труда в продуктах - его «полных затрат». Очевидно, эти последние связаны друг с другом и с удельными прямыми затратами труда (затратами «живого» труда - в противоположность овеществленному в средствах производства) теми же коэффициентами прямых затрат aij, которые фигурируют в межотраслевом балансе.

Обозначим удельные прямые затраты труда на единицу j-го продукта - lj, а полное количество содержащегося в ней труда - rj. Связывающее их уравнение имеет вид

r_j=l_j+a_1jr₁+a_2jr₂+…+a_njr_n . (1)

Или в матричной форме для всей совокупности продуктов полное количество содержащегося в ней труда составит:

R = L + А'R (2)

где R - вектор-столбец rj полное количество труда, a L вектор-столбец lj удельные прямые затраты труда. Коэффициенты же aij здесь образуют матрицу прямых технологических затрат - А', т.е. транспонированную матрицу А.

В состав полного труда, заключающегося в продуктах, входит и труд, содержащийся в используемых в его производстве основных средствах – соответственно, фондоемкости и амортизационных нормах. Тем не менее, не будем добавлять отдельное слагаемое B'R, считая, что в матрицах А и А' учтена и эта часть затрат (фондоемкость и амортизационные нормы). При таком способе записи формулы компактнее.

Математическая задача теперь состоит в том, чтобы, зная L (удельные прямые затраты труда) и А', вычислить R (полное количество труда).

R = L + А'R

Для этого перенесем неизвестные влево:

R-А'R = (Е-А')R = L

и, обратив матрицу Е-А', умножим на результат обе части слева:

R=(Е-А')-1L (3)

Заметим, что Е-А'=(Е-А)'. Обращение же транспонированной матрицы приводит к транспонированной обращенной (обратной) матрице, т. е.

(Е-А')-1=[(Е-А)-1]'=H'

(где H - матрица коэффициентов полных затрат).

Таким образом,

R=H'L (4)

R - вектор-столбец rj полное количество труда, a L вектор-столбец lj удельные прямые затраты труда.
Если же R и L представим не как столбцы, а как строки, то

R' = (H'L)' = L'H (5)

При транспонировании произведения транспонируются и переставляются множители.
В приведенной системе уравнений можно Lj заменить удельными затратами труда некоторой определенной категории.

R = L + А'R (2)

Практически можно осуществить расчет только для работников определенной категории. Понятно, что эта специальность должна быть определена для каждой отрасли. Например, физического труда, умственного труда, труда ИТР, труда работников той или иной конкретной профессиональной или профессионально-квалификационной группы (токарей, токарей такого-то разряда и т. п.). Перечень таких групп может быть составлен на базе словаря занятий, используемого в разработке переписей населения.

Отметим, что в настоящее время классификация МОТ по сквозным профессиям определяет около 700 их видов.

В США перепись 1900 г. определила 475 видов профессий (издала данные относительно 303 профессий), она основывалась на классификации 17000 типов профессий. В переписи 2000 г. определены 503 видов профессий, классификация основывалась на приблизительно 31000 типов профессий. С 2000г. SOC все определенные виды профессий классифицирует на 23 главных производственных групп. Кроме этого с 2002 NAICS определило 20 главных секторов экономики с общим количеством 1179 отраслей промышленности. При классификации предприятий для отнесения их к той или иной отрасли впервые стал работать принцип учета "подобное подобным", т.е. производит "подобные" товары и услуги с помощью "подобных" технологий. К сожалению, только в США, наконец, поняли важность данного принципа, применяемого более 20-ти лет в СССР. Ведь предприятие может производить десятки различных видов товаров и услуг, применяя различные технологии даже при производстве одного вида изделия (товаров и услуг).

Таким образом может быть получен не только в целом полный труд, содержащийся в продуктах, но и его распределение по профессиям и квалификациям.

Обозначим теперь вектор-столбец удельной заработной платы через V, а полные затраты труда в рублях заработной платы - Z. Тогда аналогично предыдущему:

Z=V+A'Z (7)
Z=(Е-A')-1V= H'V или Z'=V'H (8)

Выраженные в рублях заработной платы полные затраты труда имеют важный экономический смысл.

Если из всех цен исключить прибыль не только данного предприятия, но и всех его поставщиков, иначе говоря, если все производства снабжали бы друг друга своими продуктами по себестоимости, то себестоимости продуктов (и совпадающие с ними цены во взаимных расчетах) были бы равны этим zj. Их можно, следовательно, рассматривать как результат калькуляции себестоимости для всего народного хозяйства, исключающий надбавки прибыли. Это дает основание называть их национальной себестоимостью продуктов, т.е. их себестоимостью для общества как единого хозяйствующего субъекта.

Единственным источником стоимости является труд, состоящий из оплачиваемой работникам части и неоплачиваемой.

Первая и образует себестоимость для общества, вторая - прибыль, которая может реализоваться на любой стадии, а теоретически только при продаже предметов потребления, которыми завершается весь процесс производства.

С точки зрения измерения труда, национальная себестоимость приближает нас к учету не только его количества, выраженного в часах рабочего времени, но и его качества - в меру соответствия ему соотношений оплаты этого рабочего времени.

Чтобы получить полные затраты труда (R) на создание конечного продуктаY, надо вектор R умножить на вектор конечного спроса Y. В результате придем к одному из важнейших выводов. В самом деле,весь труд, содержащийся вконечномпродукте, равен:

R=R'Y=(L'H)Y=L'(HY)=L'X=L (9)

Или в более элементарной символике ΣRY = ΣLX.
Это означает, что полные затраты труда умноженные на создание конечного продукта (ΣRY) равнызатратамживоготруда,умноженные на обеспечивающий его валовой выпуск всех продуктов (ΣLX).

Таким образом - труд приводит в движение все производство, все его звенья на всех стадиях.

Цель понять, как зная удельные прямые затраты труда – L (доля численности занятых в объеме продаж каждой отрасли) или затраты живого труда, а также зная на сколько изменится конечный спрос - Y в следующий временной период может измениться валовой выпуск продукции - ΔX (объем продаж)

ΔХ = (Е-А')^-1(Y1-Y0)

Расчет затрат живого труда с учетом изменения валового выпуска ΔХ для всей экономики составит скалярное значение:

L=L'ΔX

То же получим как полные затраты труда на изменение конечного продукта ΔY:

R=R'ΔY

Тем не менее, для нас интересней изменение затрат труда не только в целом по экономике, но и в каждой отрасли. Для получения вектора затрат труда в каждой отрасли этого достаточно умножить вектор удельных затрат труда в каждой отрасли на вектор прогнозируемых изменений валового выпуска ΔХ для каждой отрасли:

L=LΔX

Аналогично можно дать оценку и вектора полных затрат труда в каждой отрасли:

R=RΔY

Исчисления полных трудовых затрат была предложена русским экономистом-математиком В.Дмитриевым. Для определения коэффициентов полных(cij)материальных затрат на производство единицы продукции j требуется решить систему из n уравнений с фиксированным j и i=1,…,n. Для определения всей матрицы коэффициентов полных затрат ®(cij) необходимо решить n таких систем уравнений.

Именно такой подход для исчисления полных трудовых затрат был предложен русским экономистом-математиком В. Дмитриевым.

Поэтому его можно считать основателем МОБ и всей современной системы национальной счетов во всем мире. Еще раз обращаем внимание читателя – в основе МОБ и всей современной системы национальной счетов во всем мире положен ТРУД, а не виртуальная финансовая система.

Отметим некоторые особенности экономического содержания коэффициентов полных трудовых затрат. Известно, что при общественном разделении труда любой продукт является совокупным результатом труда множества отраслей производства.

Коэффициенты полных затрат на производство продукции охватывают как непосредственные затраты живого труда на заключительной стадии изготовления продукции, так и все затраты труда на предшествующих стадиях производства данной продукции, овеществленные в потребленных средствах производства (т.е. амортизация). Таким образом, в структуре полных трудовых затрат выделяются прежде всего затраты живого труда (прямые трудовые затраты) и затраты прошлого, или овеществленного труда (косвенные трудовые затраты).

Другой путь определения полных затрат труда или национальной себестоимости это метод итераций.

В нашей задаче естественно начать вычисления с определения значений неизвестных, равных затратам живого труда. Обозначив их вектором R0, имеем

R0= L

Подставив это в правую часть, получим новые значения, которые обозначим R1

R1= L+A'L

Подставив их и обозначив новые значения неизвестных R², имеем

R²=L+A'(L+A'L)=L+A'L+A'²L

Затем получим

R3=L+A'(L+A'L+A'²L)=L+A'L+A'²L+A'³L

и т. д.
Если процесс сходится, то можем написать, что

R= L+A'L+A'²L+… = (E+A'+A'²+…)L (10)

Или, переходя от столбца R к строке

R' = L'H = L'(E+A+A²+…+Aⁿ)

Где n – определяется технологической, производственной сложностью изготовления для каждого продукта или его группы индивидуально.

Заметим, что постепенно присоединяемые к L слагаемые A'L, A'²L, A'³L и т. д. имеют вполне реальный смысл:

L - затраты живого труда в каждом производстве; A'L - затраты живого труда у поставщиков материалов; A'²L - его затраты у поставщиков этих поставщиков; A'³L - затраты у поставщиков поставщиков, поставщиков и т. д.

Это означает, что при таком вычислении полные затраты труда накапливаются суммированием труда: непосредственно в производстве продукта, в производстве применяемых средств производства или, иначе говоря, в предшествующем звене, далее - во втором предшествующем звене и т. д.

Допустим, имеется пять групп продуктов и отраслей, выпускающих данные группы продуктов, а затраты живого труда (в часах) в каждом производстве составляют:

L'= (19 18 9 48 66),

Матрица прямых затрат составляет:

Если процесс сходится, то можем написать, что

R= L+A'L+A'²L+… = (E+A'+A'²+…)L (10)

получим (округляя до целых), см. следующую таблицу.

Где
R⁰ = L - затраты живого труда в каждом производстве;
R¹ = A'L - затраты живого труда у поставщиков материалов;
R² = A'²L - его затраты у поставщиков этих поставщиков;
R³ = A'³L - затраты у поставщиков поставщиков, поставщиков и т. д.
R - полные трудовые затраты в часах на изготовление единицы конечного продукта.

Найденные результаты 15-й итерации почти приблизились к полным затратам труда R, которые могут быть вычислены с помощью алгебраических, матричных преобразований. Практически наблюдается логарифмическая зависимость – при которой по мере роста итераций косвенные затраты на каждом последующем этапе растут с меньшей скорость. Данную зависимость для всех пяти продуктов можно представить в графическом виде (см. рис. 1.38., 1.39. по данным таблицы).

Аналогичная картина наблюдается и по другим продуктам. В тоже время следует отметить важный для нас момент – в зависимости от технологической сложности изготовления тех или иных продуктов – соответственно меняется и величина косвенных затрат. Некоторые товары (на графике 3-ий продукт см. рис. 1.38.) достигают полных затрат на 6-8-ой итерациях, другим же продуктам (1-ому, 2-ому конечному продукту см. рис. 1.38.) требуется больше косвенных затрат – в нашем случае трудовых, т.к. их производство более сложное, как следствие для них требуется более высокое разделение труда. Как следствие количество итераций требуется больше. В целом это легко контролировать по уровню показателя первых производных на каждом итерационном этапе – тем самым, определяя технологическую сложность изготовления того или иного конечного продукта или его группы. Метод итераций означает, что произвольные значения неизвестных подставляются в правые части, т. е. в формулы, выражающие одни неизвестные через другие (включая и их самих). Результаты вычисления не дают, конечно, совпадения со стоящими в левых частях неизвестными. Они снова тогда подставляются вместо неизвестных в правые части (вместо прежних значений). Полученные результаты снова подставляются в правые части и т.д. Если итерационный процесс «сходится», то, в конечном счете, результат вычисления неизвестных по формулам справа оказывается все лучше совпадающим с очередными принятыми значениями. В таком случае, задав точность их определения, процесс останавливают, когда расхождение левых и правых частей становится достаточно малым. Понятно, что вопрос о сходимости описанного процесса итерации для каждого продукта связан с величиной коэффициентов затрат, образующих матрицу А.

Практически с помощью итерационного метода можно определить технологическую, производственную сложность изготовления конечного продукта, что не позволяет определить классическое алгебраическое матричное преобразование. Т.к. оно дает лишь величину косвенных затрат, но не определяет глубину латентных связей и длину технологических производственных цепочек. Ведь величина цепи и количество связей в ней неизбежно будет удлинять производственный процесс во времени и увеличивать сложность управления и риски. Естественно, если в процессе управления не контролировать и не понимать экономический смысл и важность косвенно-латентных связей и уровень их вложений, цепочек, то говорить об эффективном управлении нельзя. Это является одной из причин регулярно происходящих кризисов. Если одна из цепей или связей будет разорвана, то выпуск конечного продукта и/или их комбинации становится не возможным.

Этот момент показывает, что глобализация на данном этапе развития менеджмента даже в развитых странах это путь к пропасти. Примером может служить развал СССР, который привел к разрыву технологических производственных связей, развалу экономики всех республик.

Практически с помощью итерационного метода можно выстроить всю технологическую производственную цепочку всех поставщиков. Так, если у третьего продукта точнее его квалификационные группы количество итераций составляет 6-8 циклов, то экономически это означает, что глубина технологической цепочки всех производств поставщиков составляет цепочку из 6-8 уровней поставщиков. Понятно, что если у первого продукта его изготовление требует высокого уровня разделения труда, и как следствие технологий, то количество итераций составляет 15-16 циклов. Экономически это означает, что глубина технологической цепочки всех производств поставщиков составляет цепочку из 15-16 уровней поставщиков.

Например, если сравнить технологическую сложность банковских операций, где мультипликатор равен около 1,3-1,4 по сравнению с сельским хозяйством и производством продовольственных товаров в этих отраслях мультипликатор составляет 2,25-2,8. В тоже время оплата труда отличается более чем значительно, особенно если учесть ущерб, наносимый обществу финансовой системой из-за неквалифицированной работы их персонала.

Теоретически можно себе представить, что предприятия и в самом деле рассчитывались бы друг с другом по этой «себестоимости». Изложенный процесс итерации совершался бы тогда не только «на бумаге» через сообщаемую друг другу информацию, но и на деле - через фактические расчеты за поставки.

Это позволяет сформулировать следующую теорему.

Если с некоторого момента предприятия будут рассчитываться друг с другом за поставки по их себестоимости (у поставщиков), себестоимости продуктов будут стремиться к их национальной себестоимости, т.е. к полным затратам труда, выраженным в рублях заработной платы.

Введем поправку - если с некоторого момента предприятия будут рассчитываться друг с другом за поставки по ценам, равным себестоимости плюс прибыль, составляющая везде одинаковый процент к заработной плате, вошедшей в состав себестоимости, то цены будут стремиться в пределе к стоимости, выраженной в рублях заработной платы с прибавлением того же процента прибыли к ней. Такая стоимость как раз и соответствует содержащемуся в продуктах необходимому и прибавочному труду.

В этом случае работники производства на свой фонд заработной платы могли бы выкупить весь конечный продукт.

Для этого его цены должны были бы равняться себестоимостям - оцененный по ним конечный продукт, как мы видели, совпадает с фондом заработной платы.

Если данный подход нарушается – происходит разрыв цен и оплаты труда и неизбежный кризис – более известный в либеральных кругах, как кризис перепроизводства.
Таким образом нами доказано, что содержащийся в продуктах труд, в конечном счете, является основой и для их оценки, и как следствие определение сбалансированных цен и оплаты труда.

Отсутствия данного понимания внешней и внутренней мотивации будет приводить к росту или деградации экономики и к очередным финансовым кризисам, и неизбежно будет порождать пресловутые кризисы перепроизводства.

Широкомасштабное расширение денежной массы во всех странах улучшил финансовую, фондовую картину, но, к сожалению, это не решает проблемы, а лишь стимулирует спекулятивные игры и не более - пока цены и оплата труда не приведены в соответствие в реальных секторах экономики решить проблему кризиса невозможно. Просто сегодняшний кризис на данном этапе (2008 г.) загнан в латентное состояние. Помощь пока получили только виновники кризиса - финансово-виртуальные сектора.

Производственно-мотивационная концепция, модель Самариной
Самарина Г.П., Дорошко С.Е., Чекирда В.А. Ноосферная экономика: назад к истокам. Базисное значение труда и мотивации
– СПб.:ПИФ.com, 2008. – 338 с.